
专题选读10电磁场的相对论变换
专题选读10 电磁场的相对论变换

两个惯性系S和S”,坐标轴彼此平行,S系相对于S系 以速度)沿x轴正方向运动。下面分别画出当S系和S” 系的原点重合时,观察者分别在S系、S系时的情形。 S' Vo Vo 90 90 9 9 在S'系中,有一点电荷0在坐标原点O'处,并与S系保持 相对静止,另有一点电荷4在S'系中以速度%运动。 在S系中,运动电荷4所受的作用力?
在S系中,运动电荷 所受的作用力 q0 ? q y x 0 v q0 r θ S y′ x′ 0 v′ q0 r′ q v S′ 两个惯性系 S 和 S′ ,坐标轴彼此平行,S′系相对于 系S 以速度vr 沿x轴正方向运动。下面分别画出当 和 系的原点重合时,观察者分别在 系、 系时的情形。 S S′ S 系 S′ 在 系 中,有一点电荷q 在坐标原点 处,并与 系保持 相对静止,另有一点电荷q0 在 系中以速度 运动。 S′ O′ 0 v r S′ ′ S′

在S'系中计算点电荷g所产生的静电场' E=qr 4π8r月 9o在S'系中所受的电场力 90 F=goE qo在S系中所受的电场力 F=440-月m9西4× gr .1-B2 9×产 1-B2 4πec2r3(1-B2sin0)2 =qE+qo%×B B=
在 系中计算点电荷 S′ q 所产生的静电场 E′ r 3 π 0 4 r rq E ′ ′ ′ = ε r r q 0在 系中所受的电场力 S′ EqFr r ′ = ′ 0 2322 2 32 0 2322 00 2 3 0 0 )sin1( 1 4)sin1( π 1 4 π θβ β θβ ε β ε − −× ×+ − − ⋅= rc rvq vq r rq qF r r r r r BvqEq r r r 000 ×+= c v β = y′ x′ 0 v′ q 0 r′ q v r S′ q 0在 系中所受的电场力 S

E=- gr 1-B2 πe3(1-B2sin28)32 c于0-P品rx厅 B=_ 1-B2 F=E+,成。×B 讨论 (1)运动电荷q的电场E 1-B2 (1-B2sin20)2 当电荷q以低速运动时B='<1 电场分布结果与静电场一样,电场线保留中心对称性
Ev rc c rvq B r r r r r ×= − −× = 22322 2 32 0 1 )sin1( 1 4 θβ β πε 2322 2 3 0 )sin1( 1 4 θβ β πε − − ⋅= r rq E r r BvqEqF r r r r 000 ×+= 讨论 2322 2 )sin1( 1 θβ β − − <<= 1 c v 当电荷q以低速运动时 β 电场分布结果与静电场一样,电场线保留中心对称性 (1)运动电荷q 的电场 Er

随着电荷运动速度的增大,这种对称性被破坏 在运动速度方向的电场,0=0,因子为(1-B2) E变小,电场线变疏。 垂直于运动速度方向的电场,日-乃,因子为 E变大,电场线变密。 -B
在运动速度方向的电场, ,因子为 E 变小,电场线变疏。 θ = 0 )1( 2 − β 垂直于运动速度方向的电场, ,因子为 E 变大,电场线变密。 随着电荷运动速度的增大,这种对称性被破坏 2 π θ = 2 1 1 − β

当B→1时,电场线将无限密集于电荷运动的垂直方向。 (2)运动电荷g的磁场B 使一探测电荷q0静止于电场和磁场均存在的空间P点,测 量它的受力 此力为电场力F
当 时,电场线将无限密集于电荷运动的垂直方向。 β → 1 (2) 运动电荷q 的磁场 B r 使一探测电荷 静止于电场和磁场均存在的空间 P点,测 量它的受力 q 0 Fe r 此力为电场力

再使9以某一速度。通过P点,测出合力 则磁场力 F=F-尼 改变,方向测量磁场力,P点处有一个特殊方向, 当,沿此方向通过P点时,不管其速率多大,测得的 磁场力恒为零,则磁场B就在此方向上 当在垂直此方向通过P点时,磁场力有最大值Fmax, 于是,我们定义磁感应强度B的大小为 B= F=96×B 90vo
改变 方向测量磁场力,P 点处有一个特殊方向, 当 沿此方向通过 P 点时,不管其速率多大,测得的 磁场力恒为零,则磁场 就在此方向上 0 v r 0 v r B r m FFF e r r r −= 当在垂直此方向通过 P 点时,磁场力有最大值 , 于是,我们定义磁感应强度 的大小为 Fmax B r 再使 以某一速度 通过 P 点,测出合力 则磁场力 q 0 0 v r F r 00 max vq F B = BvqF r r r 00m ×=
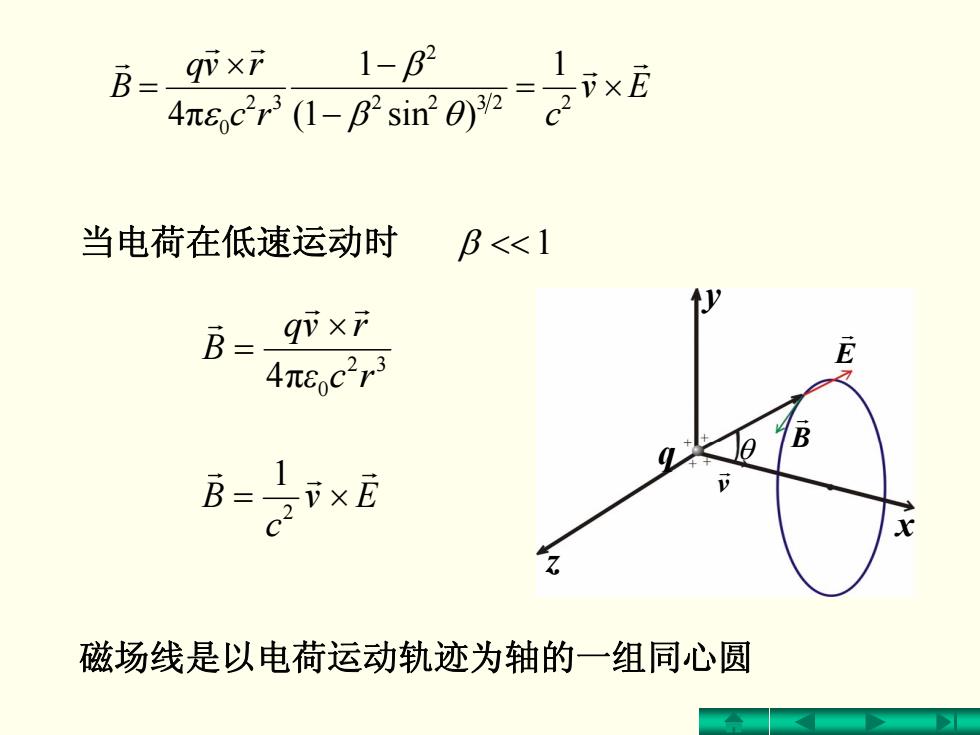
B=_qixi 1-B2 4,cFI-B产sin。×E 当电荷在低速运动时 B<<1 B= ×F 4πec2r E B B=×E 磁场线是以电荷运动轨迹为轴的一组同心圆
Ev rc c rvq B r r r r r ×= − −× = 22322 2 32 0 1 )sin1( 1 4π θβ β ε 当电荷在低速运动时 β << 1 32 π 0 4 ε rc rvq B r r r × = Ev c B r r r ×= 2 1 磁场线是以电荷运动轨迹为轴的一组同心圆 θ y x z B r E r q v r

(3)磁场力是对电场力的一种相对论修正 S 92 92 91 在S'中,4、92相对静止,仅观测到静电场力 F= 1 9192 4π800 在S中,0=元/2,既有电场力 Fe= 9192 4π62V1-B 又有磁场力 Fn-992 4πE,c'nV1-B
2 q 1 q 1 q 2 q y y′ x x′ v v 0r 0r v S S′ 在 中, 、 相对静止,仅观测到静电场力 S′ q1 q2 2 0 21 0 e 4π 1 r qq F ε ′ = 在 S 中, ,既有电场力 θ = π 2 2 2 00 21 e 1 1 4πε − β = r qq F 又有磁场力 2 2 0 2 0 2 21 m 1 1 4πε − β = rc vqq F (3)磁场力是对电场力的一种相对论修正

两个场力的比值 作用在电荷94或92上的合力为 B2 在高速运动中,B→1,此时磁场力与电场力有相同数量 级,磁场力将起到与电场力相当的作用 在两根平行通电导线之间 在通电导线中,导线中电子的漂移速度极小,大为 104ms数量级, (/c)2≈1025
两个场力的比值 2 e m )( c v F F = 作用在电荷 或 上的合力为 q1 q2 2 2 00 21 me 1 4 β πε −⋅=−= ⋅ rqq FFF 在高速运动中, ,此时磁场力与电场力有相同数量 级,磁场力将起到与电场力相当的作用 β →1 在两根平行通电导线之间 在通电导线中,导线中电子的漂移速度极小,大约为 10-4ms-1数量级, 2 25 10)( − cv ≈