深圳大学：《系统动力学》课程教学资源（PPT课件）第二讲 刚性机械系统动力学（单自由度系统）

机械动力学分析与设计 刚性机械系统动力学(1) --单自由度系统

刚性机械系统动力学(1) ---单自由度系统 机械动力学分析与设计

刚性机械系统 实际问题的简化： 1不考虑弹性变形，认为构件是绝对刚体 2不考虑运动副中的间隙，认为运动副中 密切接触 3不考虑运动副中的摩擦力影响 4 不计构件尺寸的加工误差

刚性机械系统 实际问题的简化： 1 不考虑弹性变形，认为构件是绝对刚体 2 不考虑运动副中的间隙，认为运动副中 密切接触 3 不考虑运动副中的摩擦力影响 4 不计构件尺寸的加工误差

单自由度系统 一个活动构件 多个构件 构件通过运 自由度=1 动副约束

单自由度系统 一个活动构件 多个构件 构件通过运 动副约束 自由度=1

动力学方程的建立 用达朗伯原理 例：平面四杆机构： 3N个方程 N=3 未知量中 方程数：n=9 有约束反 力 未知数：8个约束反 力十1个角加速度 分为若干个隔离体，建立每一个构件的动力学方程 质心X2y 构件运动 主动力 动力学方程 转角P, 约束反力

动力学方程的建立 用达朗伯原理 3N个方程 未知量中 有约束反 力 例：平面四杆机构： N=3 方程数: n=9 未知数：8个约束反 力＋1个角加速度 分为若干个隔离体，建立每一个构件的动力学方程 , i i 质心 x y 转角 i 构件运动 主动力 约束反力 动力学方程

动力学方程的建立 用达朗伯原理 例：平面四杆机构： 3N个方程 N=3 未知量中 方程数：n=9 约束反 力 未知数：8个约束反 力+1个角加速度 用拉格朗日方程 个方程

动力学方程的建立 用达朗伯原理 3N个方程 未知量中 有约束反 力 用拉格朗日方程 1 个方程 例：平面四杆机构： N=3 方程数: n=9 未知数：8个约束反 力＋1个角加速度

用拉氏方程建立动力学方程 例：平面四杆机构： N=3 方程数：n=9 未知数：8个约束反 力+1个角加速度 单自由度系统 q-第r个广义坐标 定义原动件转角二 )广义坐标 E-系统动能 U-系统势能 动能十势能十功 Q-对第个广义坐标的广义力 (热能、电能)

用拉氏方程建立动力学方程 例：平面四杆机构： N=3 方程数: n=9 未知数：8个约束反 力＋1个角加速度 单自由度系统 定义原动件转角 1 广义坐标 qr--第r 个广义坐标 E--系统动能 U--系统势能 Qr--对第个广义坐标的广义力 动能＋势能＋功 (热能、电能)

用拉氏方程建立动力学方程 d aE aU dt aqr aqr aq r=1,2..W 此处N=1 -区w-交） + 可用一个构件等效一 等效转动惯量J。 动能不变原则

用拉氏方程建立动力学方程       =  + = = n i n i i i i i E m v J 1 1 2 2 2 1  =                 +         = n i i i i i J v m 1 2 1 2 1 2 1 2 1     等效转动惯量—Je r N Q q U q E q E dt d r r r r 1,2... ( ) . = =   +   −   此处 N=1 可用一个构件等效— —动能不变原则

用拉氏方程建立动力学方程 25,85+8-0 dt aqr aqr aqr r=1,2.W 此处N=1 ·在动能相等的前提下，将系统的惯性参数等效为一个构件 Je是机构位置的函数 等效转动惯量变化的物理意义：由于系统固有的运动特性 引起的系统动能变化

用拉氏方程建立动力学方程 2 1 1 2 E J = e  等效转动惯量—Je r N Q q U q E q E dt d r r r r 1,2... ( ) . = =   +   −   此处 N=1 2 2 2 1 1 1 1 1 2 n i i e i i i v J m J   =         = +                •等效转动惯量变化的物理意义：由于系统固有的运动特性 引起的系统动能变化。 •Je是机构位置的函数 •在动能相等的前提下，将系统的惯性参数等效为一个构件

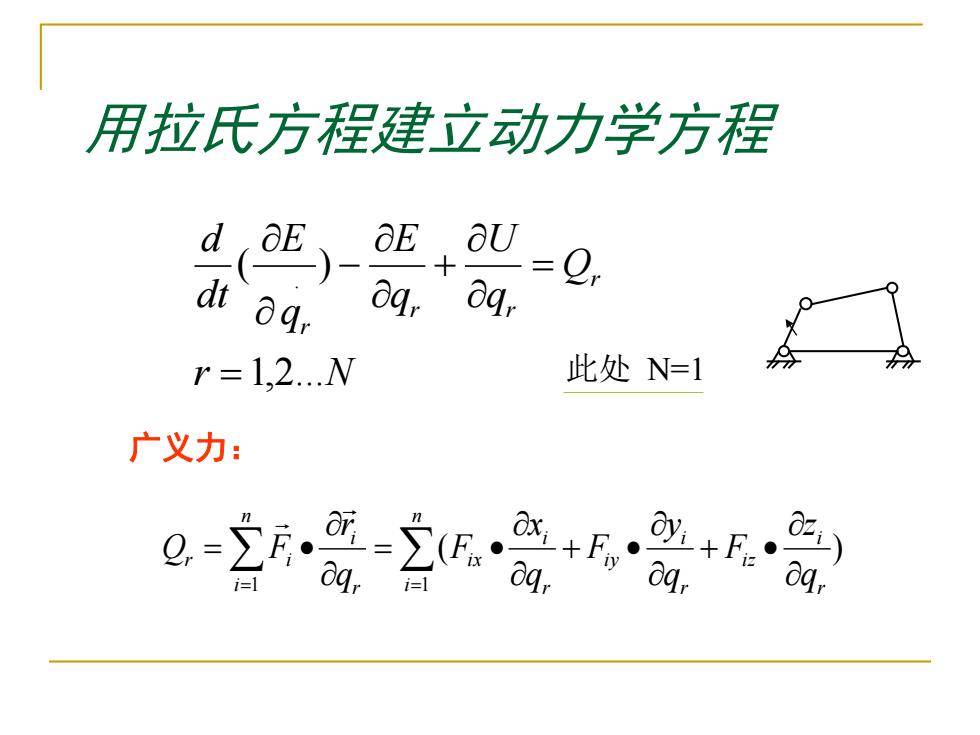
用拉氏方程建立动力学方程 0D\一 oE U=0, dt aqr aq, r=1,2..N 此处N=1 广义力： ayFqr Faqr y)

用拉氏方程建立动力学方程 ( ) 1 1 r i i z r i i y r i n i i x r i n i r i q z F q y F q x F q r Q F   + •   + •   = •   = •  = =   r N Q q U q E q E dt d r r r r 1,2... ( ) . = =   +   −   此处 N=1 广义力：

广义力 0) i=1 i=l xFoyoar ay+f:°0qr 成立 8q,ag. M.-r(占)csa,±2M,(%) 机械原理—功率不变原则： M.0=) 以ea±空Ma V-着力点速度 -着力点力的方向与速度夹角 广义力—等效力矩 01

  = =  =  q i i i p i Me Fi Vi i M 1 1 1  cos    = = =  q i i i p i i i e i M V M F 1 1 1 1 ( ) cos ( )     Vi -- 着力点速度 -- 着力点力的方向与速度夹角 机械原理——功率不变原则： 广义力 ( ) 1 1 r i i z r i i y r i n i i x r i n i r i q z F q y F q x F q r Q F   + •   + •   = •   = •  = =   广义力——等效力矩   = = =  q i i i p i i i e i M V M F 1 1 1 1 ( ) cos ( )     i i r r r r q q   =  