
高阶系统的时域分析 定义:用高阶微分方程描述的系统称为高阶系 统。 由于求高阶系统的时间响应很是困难,所以通常总 是将多数高阶系统化为一、二阶系统加以分析。 通常对于高阶系统来说,离虚轴最近的一个或两个 闭环极点在时间响应中起主导作用,而其他离虚轴 较远的极点,他们在时间响应中相应的分量衰减较 快,只起次要作用,可以忽略
高阶系统的时域分析 定义:用高阶微分方程描述的系统称为高阶系 统。 由于求高阶系统的时间响应很是困难,所以通常总 是将多数高阶系统化为一、二阶系统加以分析。 通常对于高阶系统来说,离虚轴最近的一个或两个 闭环极点在时间响应中起主导作用,而其他离虚轴 较远的极点,他们在时间响应中相应的分量衰减较 快,只起次要作用,可以忽略
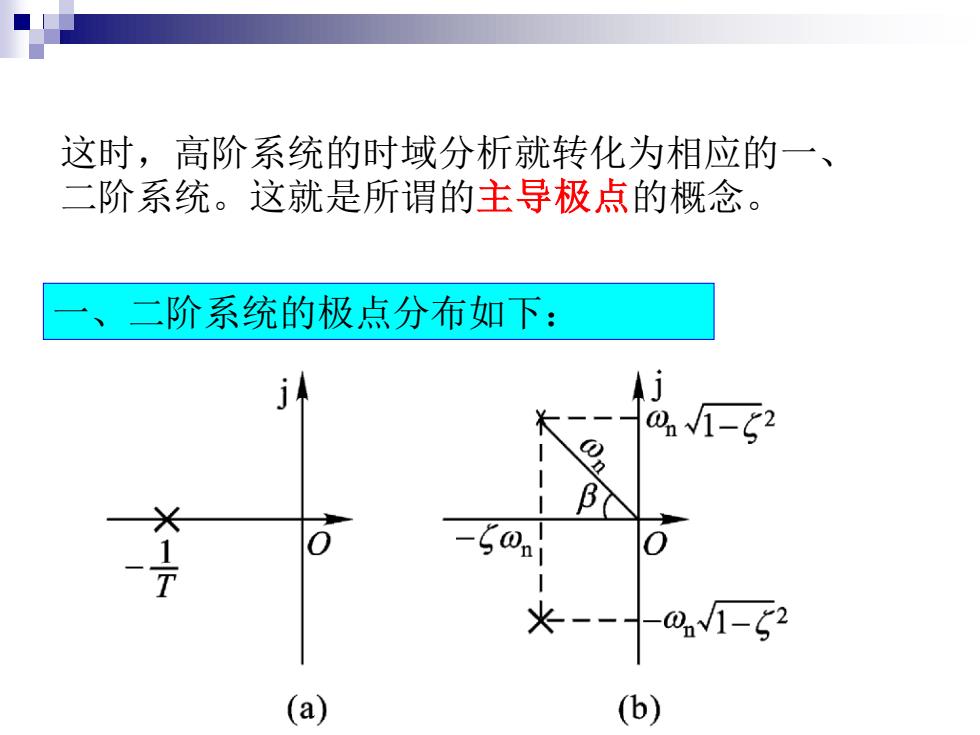
这时,高阶系统的时域分析就转化为相应的一、 二阶系统。这就是所谓的主导极点的概念。 一、二系统的极点分布如下: i j 01-2 B -50l 火 -01-ξ2 (a) (b)
这时,高阶系统的时域分析就转化为相应的一、 二阶系统。这就是所谓的主导极点的概念。 一、二阶系统的极点分布如下:

高阶系统的暂态响应 1.典型三阶系统的阶跃响应 典型三阶系统是最简单的高阶系统,是在典型二阶系统基础上增加一 个惯性环节构成,其传递函数为: a (s)=+2X5+2)(T3+1 可改写为 一w253 设0<℃<1 p(s)=(G2+2gw9干g)(3-59)5 引入:B=gw. -53 K =(5-51)(s-52)(5 单位阶跃响应为: eop ()2)(-2)os1 +5IS(3-2+1lsnV个-5at 1-2 e 9(3-2)+1 (t≥0) 图3-33典型三阶系统的零极点分布
高阶系统的暂态响应 可改写为 :设 0< <1 引入: 单位阶跃响应为: 1. 典型三阶系统的阶跃响应 典型三阶系统是最简单的高阶系统,是在典型二阶系统基础上增加一 个惯性环节构成,其传递函数为:
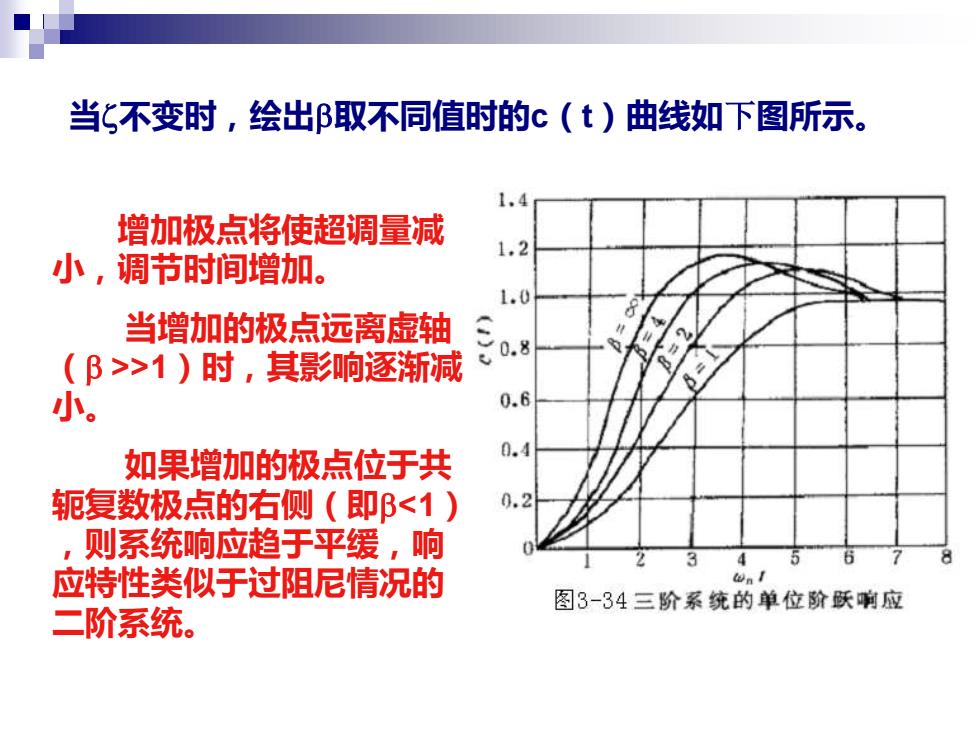
当不变时,绘出β取不同值时的c(t)曲线如下图所示。 增加极点将使超调量减 1.2 小,调节时间增加。 1.0 co) 当增加的极点远离虚轴 0.8 (β>1)时,其影响逐渐减 B=2 小。 0.6 0.4 如果增加的极点位于共 轭复数极点的右侧(即B<1) 0.2 则系统响应趋于平缓,响 4 应特性类似于过阻尼情况的 n I 图3-34三阶系统的单位阶跃喇应 二阶系统
当不变时,绘出取不同值时的c(t)曲线如下图所示。 增加极点将使超调量减 小,调节时间增加。 当增加的极点远离虚轴 ( >>1)时,其影响逐渐减 小。 如果增加的极点位于共 轭复数极点的右侧(即<1) ,则系统响应趋于平缓,响 应特性类似于过阻尼情况的 二阶系统

高阶系统暂态响应分析 (1)高阶系统的单位阶跃响应 一般高阶系统的传递函数为: Φ(s)= bosm+b1sm-1十…十bm-1s+bn s"+a1s”-1+…十an-1s十an 改写为零、极点形式: Φ(s)= K1(s-z1)(s一22)(s-之m) (s-S1)(s一S2)…(s-sn) 当单位阶跃信号输人时,其系统的阶跃响应拉氏变换式为: K:ii (s) C(s)= si(s-s)Ⅱ(s2+25aas+) -+会+ Ba(s+S4w)十C4w地√1一S s2十25wm5十o
高阶系统暂态响应分析 (1)高阶系统的单位阶跃响应 一般高阶系统的传递函数为: 改写为零、极点形式: 当单位阶跃信号输人时,其系统的阶跃响应拉氏变换式为:

对上式进行拉氏反变换,得 c()=+eBe-cos1 S是ant +∑Cxei'sin√1-t(t≥0) 高阶系统的单位阶跃响应是由+1项(每一项称为高阶系 统单位阶跃响应的一个分量)组成,每个分量对应于C(S)的一 个极点。 每个单极点对应一阶系统响应分量,一对共轭复数极点 对应一个二阶振荡系统的响应分量。 如果系统所有的闭环极点都具有负的实部,即所有闭环 极点都在S平面的左半部,那么随着时间的增长,c()中除第 一项外的项都趋于零,且闭环极点距虚轴越远,对应的响应分 量衰减得越快
对上式进行拉氏反变换,得 高阶系统的单位阶跃响应是由n+1项(每一项称为高阶系 统单位阶跃响应的一个分量)组成,每个分量对应于C(s)的一 个极点。 每个单极点对应一阶系统响应分量,一对共轭复数极点 对应一个二阶振荡系统的响应分量。 如果系统所有的闭环极点都具有负的实部,即所有闭环 极点都在S平面的左半部,那么随着时间的增长,c(t)中除第 一项外的项都趋于零,且闭环极点距虚轴越远,对应的响应分 量衰减得越快
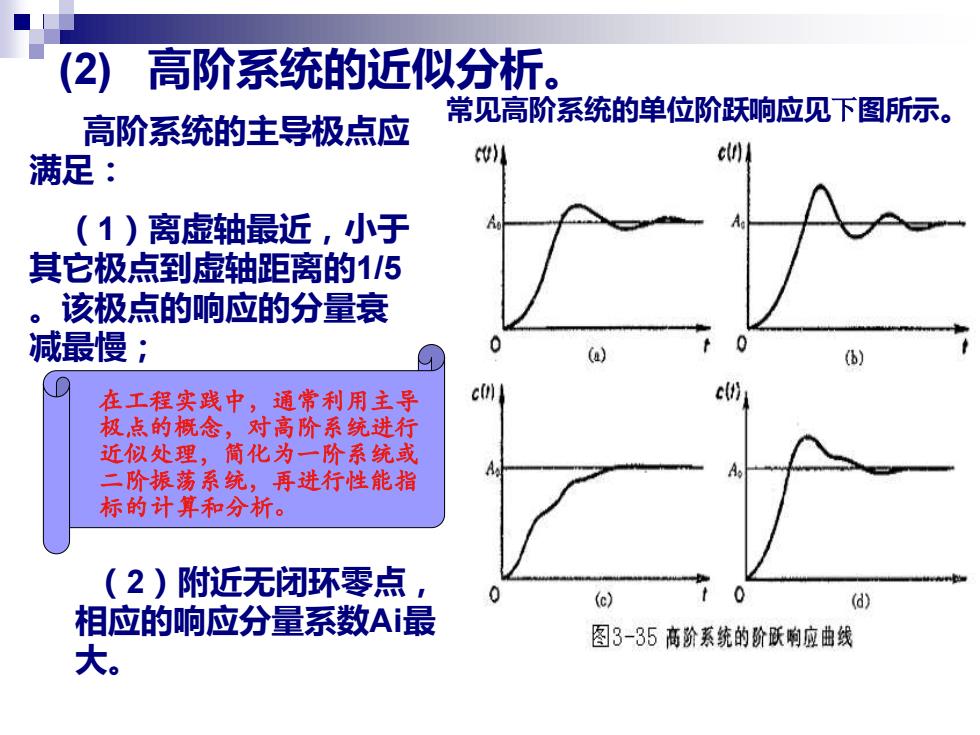
高阶系统的近似分析。 常见高阶系统的单位阶跃响应见下图所示。 高阶系统的主导极点应 满足 c(n (1)离虚轴最近,小于 其它极点到虚轴距离的115 。该极点的响应的分量衰 减最慢; 在工程实践中,通常利用主导 c(n c 极,点的概念,对高阶系统进行 近似处理,简化为一阶系统或 二阶振荡系統,再进行性能指 标的计算和分析。 (2)附近无闭环零点, (c) 0 (d) 相应的响应分量系数A最 图3-35高阶系统的阶跃响应曲线 大
(2) 高阶系统的近似分析。 常见高阶系统的单位阶跃响应见下图所示。 高阶系统的主导极点应 满足: (1)离虚轴最近,小于 其它极点到虚轴距离的1/5 。该极点的响应的分量衰 减最慢; (2)附近无闭环零点, 相应的响应分量系数Ai最 大。 在工程实践中,通常利用主导 极点的概念,对高阶系统进行 近似处理,简化为一阶系统或 二阶振荡系统,再进行性能指 标的计算和分析

主导极点可能是单个实数极点,也 可能是共轭复数极点。前者可用一阶系 统近似代替,后者可用二阶振荡系统近 似代替
主导极点可能是单个实数极点,也 可能是共轭复数极点。前者可用一阶系 统近似代替,后者可用二阶振荡系统近 似代替

系统稳定性分析 一、 系统稳定的概念 口是指系统当扰动作用消失后,由初始偏差 状态恢复到原平衡状态的性能。 ▣若系统能恢复平衡状态,就称该系统是稳 定的,若系统在扰动作用消失后不能恢复 平衡状态,且偏差越来越大,则称系统是 不稳定的
一、系统稳定的概念 ❑ 是指系统当扰动作用消失后,由初始偏差 状态恢复到原平衡状态的性能。 ❑ 若系统能恢复平衡状态,就称该系统是稳 定的,若系统在扰动作用消失后不能恢复 平衡状态,且偏差越来越大,则称系统是 不稳定的。 系统稳定性分析

■系统稳定的充分必要条件是: 系统的特征方程的所有根都具有负实部, 或者说都位于S平面的虚轴之左。 注:拉氏变换性质中的终值定理的适用条件: SE(S在S平面的右半平面解析,就是上面稳定条 件的另一种表示,即特征方程的所有根S,位于S平 面的虚轴之左
◼ 系统稳定的充分必要条件是: 系统的特征方程的所有根都具有负实部, 或者说都位于S平面的虚轴之左。 注:拉氏变换性质中的终值定理的适用条件: SE(S)在S平面的右半平面解析,就是上面稳定条 件的另一种表示,即特征方程的所有根Si位于S平 面的虚轴之左