
第六章输电线路和绕组中的波过程 正常工作电压:直流、正弦交流; 大气过电压 雷电过电压 感应过电压 过电压 内部过电压 操作过电压 谐振过电压 电力系统中的过电压通常以行波的形式出现 波过程的一些基本概念 1、什么是波过程 电力系统是各种电气设备经线路连接成一个保证安全发供电的整体。 从电路的观点看,除电源外,可以用一个R、L、C三个典型元件的不同组 合来表示,但这种电路仅适宜于电源频率较低,线路实际长度小于电源 波长条件之下。 例如:工频电压下,波长6000km,而220kV高压输电长度200-250km 因此,线路不长时,电路中的元件可作为集中参数处理
第六章 输电线路和绕组中的波过程 正常工作电压:直流、正弦交流; 电力系统中的过电压通常以行波的形式出现 波过程的一些基本概念 1、什么是波过程 电力系统是各种电气设备经线路连接成一个保证安全发供电的整体。 从电路的观点看,除电源外,可以用一个R、L、C三个典型元件的不同组 合来表示,但这种电路仅适宜于电源频率较低,线路实际长度小于电源 波长条件之下。 例如:工频电压下,波长6000km,而220kV高压输电长度200-250km 因此,线路不长时,电路中的元件可作为集中参数处理

但若线路或设备的绕组在雷电波作用下,由于雷电波的波 头时间仅为1.2微秒,则雷电压(或雷电流)由零上升到最 大幅值时,雷电波仅在线路上传播360m,因此对长达几十 乃至几百公里的输电线路,在同一时间,线路上的雷电压 (或雷电流)的幅值是不一样的。 线路中电压和电流不仅与时间有关,而且还与离该点距离 有关。同时线路、绕组有电感、对地有电容,绕组匝间又 存在电容,因此输电线路和绕组就不能用一个集中参数元 件来代替。 而分布参数的过渡过程实际上就是电磁波的传播过程,我 们简称为波过程。其实际上也是导线周围空间存储电磁波 的过程
但若线路或设备的绕组在雷电波作用下,由于雷电波的波 头时间仅为1.2微秒,则雷电压(或雷电流)由零上升到最 大幅值时,雷电波仅在线路上传播360m,因此对长达几十 乃至几百公里的输电线路,在同一时间,线路上的雷电压 (或雷电流)的幅值是不一样的。 线路中电压和电流不仅与时间有关,而且还与离该点距离 有关。同时线路、绕组有电感、对地有电容,绕组匝间又 存在电容,因此输电线路和绕组就不能用一个集中参数元 件来代替。 而分布参数的过渡过程实际上就是电磁波的传播过程,我 们简称为波过程。其实际上也是导线周围空间存储电磁波 的过程
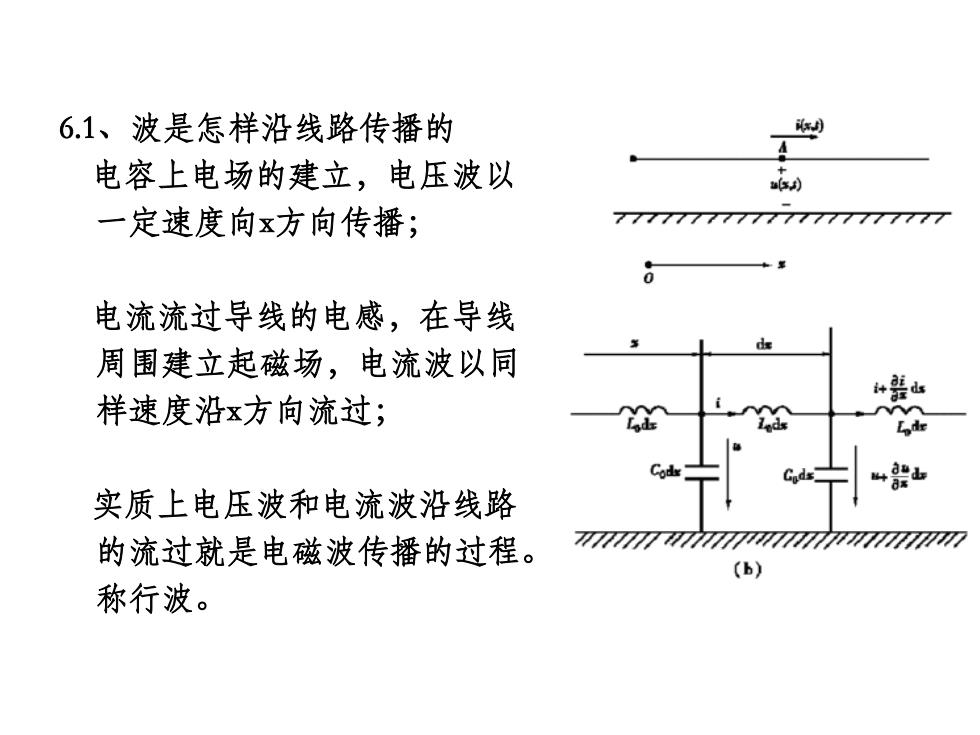
6.1、波是怎样沿线路传播的 电容上电场的建立,电压波以 a60 一定速度向x方向传播; 7777777777777777777777 电流流过导线的电感,在导线 周围建立起磁场,电流波以同 样速度沿x方向流过; 实质上电压波和电流波沿线路 的流过就是电磁波传播的过程。 (b) 称行波
6.1、波是怎样沿线路传播的 电容上电场的建立,电压波以 一定速度向x方向传播; 电流流过导线的电感,在导线 周围建立起磁场,电流波以同 样速度沿x方向流过; 实质上电压波和电流波沿线路 的流过就是电磁波传播的过程。 称行波
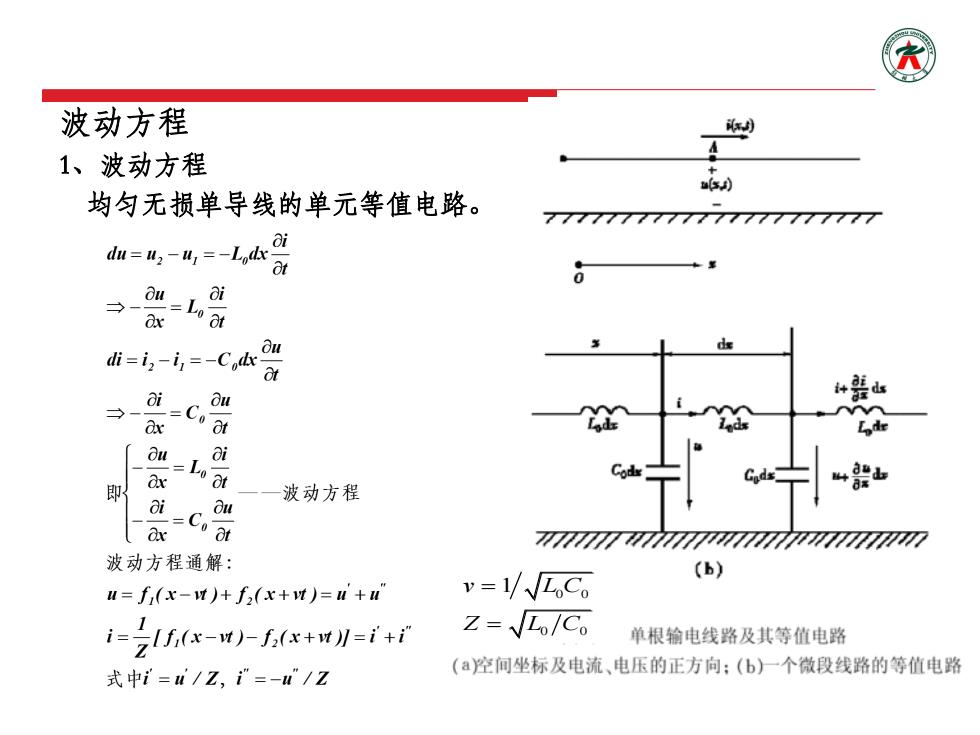
波动方程 制 1、波动方程 ● 均匀无损单导线的单元等值电路。 7777777777777777777777 du=42-4=-Lk t ai Lo ot di=i-i=-Codx t i-CoOt Ou 「a ai 即 波动方程 ai ax - 波动方程通解: (B) u=f(x-v)+f2(x+v)=n+u v=/√LC i=名xfx*m以=+i Z=√/Co 单根输电线路及其等值电路 式中i=l/Z,i”=-”/Z (空间坐标及电流、电压的正方向:(b)一个微段线路的等值电路
波动方程 1、波动方程 均匀无损单导线的单元等值电路。 0 0 0 0 v L C 1 Z L C

2、波动方程通解的物理意义 (1)电压和电流的解包括两部分 函数山=f,(x-t)表示一个任意形状并以速度v向x正方向运动的电压前行波; 函数u=f,(x+t)表示一个任意形状并以速度v向x负方向运动的电压反行波; 与此类似,为电流前行波,为电流反行波。 (2)电压波和电流波之间通过波阻抗联系 i'=w/Z,i'=-w”/Z 不同极性的行波向不同方向传播,需要规定一定的正方向。 电压波符号只决定导线对地电容上相应电荷符号,和运动方向无关。 电流波的符号不但与相应的电荷符号有关,而且与运动方向有关。 一般,以正电荷沿着x正方向运动所形成者为正电流波。 (3)分布参数的波阻抗与集中参数电路中的电阻有本质区别 波阻抗表示具有同一方向电压波和电流波大小的比值
2、波动方程通解的物理意义 (1)电压和电流的解包括两部分 函数 表示一个任意形状并以速度v向x正方向运动的电压前行波; 函数 表示一个任意形状并以速度v向x负方向运动的电压反行波; 与此类似, 为电流前行波, 为电流反行波。 (2)电压波和电流波之间通过波阻抗联系 不同极性的行波向不同方向传播,需要规定一定的正方向。 电压波符号只决定导线对地电容上相应电荷符号,和运动方向无关。 电流波的符号不但与相应的电荷符号有关,而且与运动方向有关。 一般,以正电荷沿着x正方向运动所形成者为正电流波。 (3)分布参数的波阻抗与集中参数电路中的电阻有本质区别 波阻抗表示具有同一方向电压波和电流波大小的比值

波阻抗与电阻 相似处: 与电源频率无关 导线上既有前行波,又有反行波时: 从电源吸收的功率相同 uu tu u+u 不同处: Z卡Z 波阻抗只是比例,无长度概念 ii+i” u -u 波阻抗从电源吸收的能量未消耗 i'=u'/Z,i"=-u/Z (4)波阻抗的数值只和导线单位长度的L0、C0有关,而与线路长度无关。 (5)电流波的传播方向电流的流动方向不是同一事物;行波沿导线的传 播速度亦与带电粒子在导线中的运动速度不同,电子的绕核速度00 米每秒左右,定向移动更慢。区别出横向位移和纵向位移。 (6)波阻抗吸收的功率以电磁能存储在导线周围媒介中,电阻吸收的功 率转化为热消耗掉
导线上既有前行波,又有反行波时: (4)波阻抗的数值只和导线单位长度的L0、C0有关,而与线路长度无关。 (5)电流波的传播方向电流的流动方向不是同一事物;行波沿导线的传 播速度亦与带电粒子在导线中的运动速度不同,电子的绕核速度100 米每秒左右,定向移动更慢。区别出横向位移和纵向位移。 (6)波阻抗吸收的功率以电磁能存储在导线周围媒介中,电阻吸收的功 率转化为热消耗掉。 波阻抗与电阻 相似处: 与电源频率无关 从电源吸收的功率相同 不同处: 波阻抗只是比例,无长度概念 波阻抗从电源吸收的能量未消耗
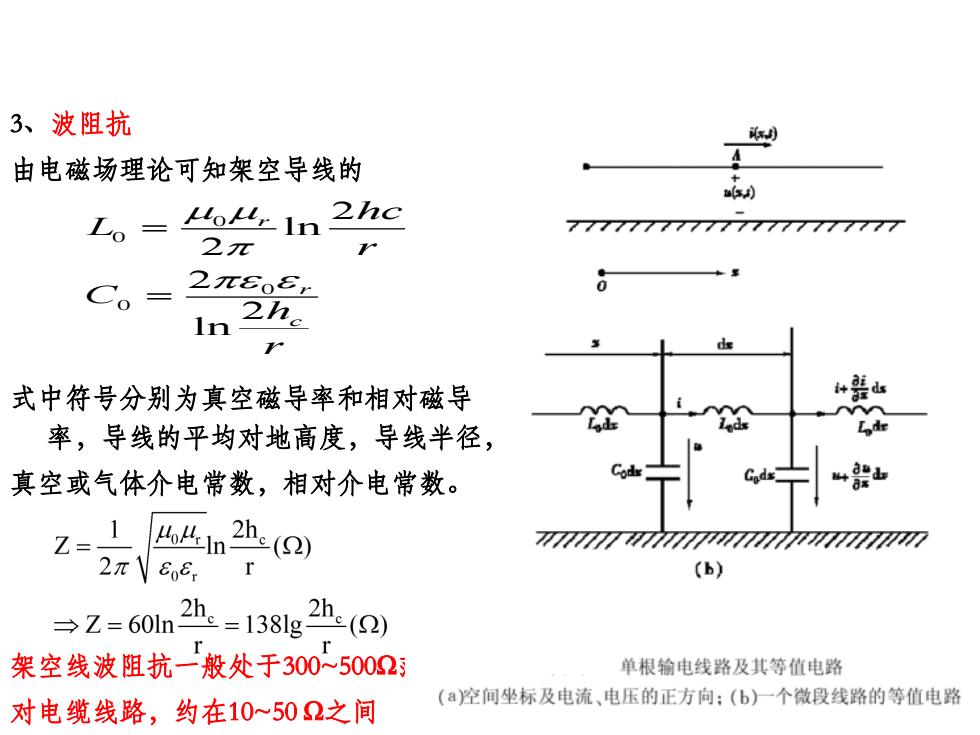
3、波阻抗 由电磁场理论可知架空导线的 a0月) Lo Lolir In 2hc 7777777777777777777777 2元 K Co= 27πE0E: 2he In 式中符号分别为真空磁导率和相对磁导 率,导线的平均对地高度,导线半径, 真空或气体介电常数,相对介电常数。 Z= 1 4n2h( r (B) →Z=60n24-1381g2h(2 架空线波阻抗一般处于300~5002 单根输电线路及其等值电路 对电缆线路,约在10~502之间 (空间坐标及电流、电压的正方向:(b)一个微段线路的等值电路
3、波阻抗 由电磁场理论可知架空导线的 式中符号分别为真空磁导率和相对磁导 率,导线的平均对地高度,导线半径, 真空或气体介电常数,相对介电常数。 架空线波阻抗一般处于300~500Ω范围内; 对电缆线路,约在10~50 Ω之间 0 0 0 0 2 ln 2 2 2 ln r r c hc L r C h r

4、波速度 V=x tLo/Co →V= _3×10 (m/s) √44,e8,V,e, 从上式可见: 波的传播速度与导线的几何尺寸、悬挂 高度无关,而仅由导线周围介质确定。 对架空线:e,=1,4,=1,v=3X108m/s。 对电缆:e,=4,h,=1,v=1.5×108m/s
4、波速度 从上式可见: 波的传播速度与导线的几何尺寸、悬挂 高度无关,而仅由导线周围介质确定。 对架空线:εr=1,μr=1,v=3×108m/s。 对电缆: εr=4,μr=1,v=1.5×108m/s
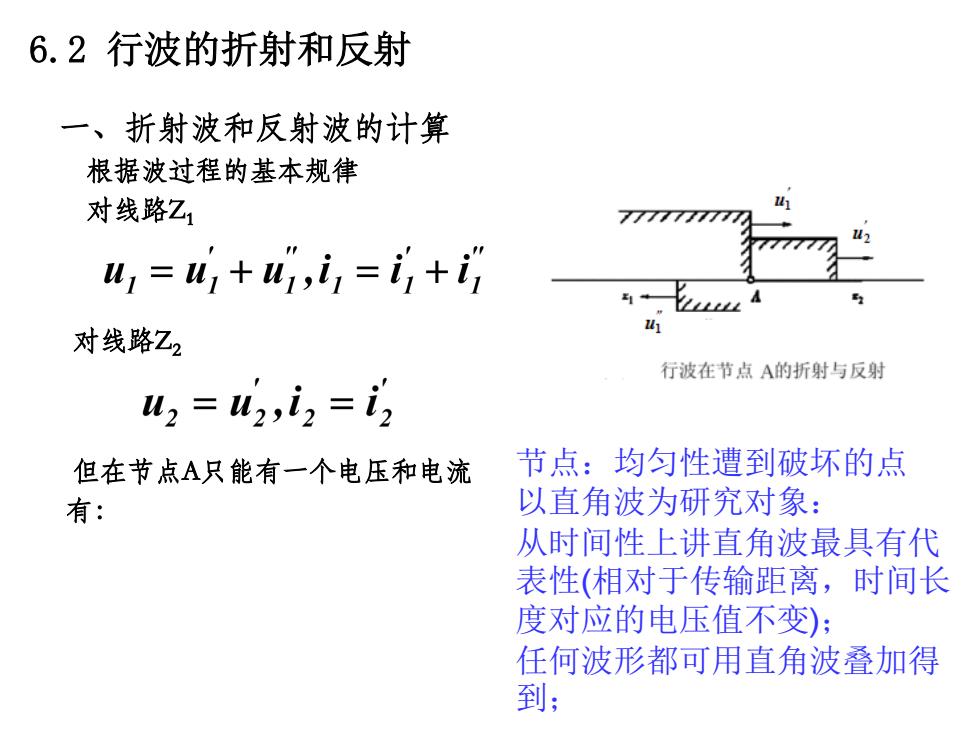
6.2行波的折射和反射 一、折射波和反射波的计算 根据波过程的基本规律 对线路Z1 7777777777 41=41+41,i1=+i 对线路Z2 行波在节点A的折射与反射 u2=u2,2= 但在节点A只能有一个电压和电流 节点:均匀性遭到破坏的点 有: 以直角波为研究对象: 从时间性上讲直角波最具有代 表性(相对于传输距离,时间长 度对应的电压值不变): 任何波形都可用直角波叠加得 到
一、折射波和反射波的计算 根据波过程的基本规律 对线路Z1 对线路Z2 但在节点A只能有一个电压和电流 有: 6.2 行波的折射和反射 节点:均匀性遭到破坏的点 以直角波为研究对象: 从时间性上讲直角波最具有代 表性(相对于传输距离,时间长 度对应的电压值不变); 任何波形都可用直角波叠加得 到;

ui uz,in iz 41+41=42 → iti=i 2= 2Z34=a.4 Z,+Z2 → ,= Z2-Z14,=B41 Z1+Z2 式中am一电压折射系数0≤am≤2); B,一电压反射系数(1≤B,≤I); 1+B=ao