
Log 控制系统的频率特性 频率特性 频率响应的Nyquist图 频率响应的Bode图 控制系统的闭环频率响应
L o g o 控制系统的频率特性 频率特性 频率响应的Nyquist 图 频率响应的Bode图 控制系统的闭环频率响应

时域分析法研究系统的各种动态与稳态性 能比较直观、准确 缺点是: 1.当某些系统工作机理不明了时,数学模型难以确定, 因而无法分析系统性能。 2.当系统的响应不能满足技术要求时,也不容易确 定应该如何调整系统来获得预期效果
时域分析法研究系统的各种动态与稳态性 能比较直观、准确 缺点是: 1. 当某些系统工作机理不明了时,数学模型难以确定, 因而无法分析系统性能。 2. 当系统的响应不能满足技术要求时,也不容易确 定应该如何调整系统来获得预期效果

频域法是利用频率特性研究自动控制系统的一种古典方法 1)应用My9uist(奈奎斯特)稳定性判据,可以根据系统的开环频率特性, 研究闭环系统的稳定性,而不必求特征方程的根。 2))对于二阶系统,频率响应和瞬态响应的性能指标之间有确定的对应关系 而高阶系统也存在类似的关系。因为系统的频率特性与系统参数、结构之 间有着密切关系,所以可以利用研究频率特性的方法,把系统的参数、结 构变化和瞬态响应性能指标之间联系起来。 3)频率特性有明确的物理意义,很多元件的这一特性都可以用实验的方法 确定,这对难于分析其物理规律来列出微分方程的元部件和系统,有很重 要的工程实际意义。 4) 频率特性分析法不仅适用于线性系统,而且可以推广到某些非线性系统 5)当系统在某些频率范围存在着严重噪声时,应用频率法,可以设计出能 够很好抑制这些噪声的系统
频域法是利用频率特性研究自动控制系统的一种古典方法 1) 应用Nyquist(奈奎斯特)稳定性判据,可以根据系统的开环频率特性, 研究闭环系统的稳定性,而不必求特征方程的根。 2) 对于二阶系统,频率响应和瞬态响应的性能指标之间有确定的对应关系, 而高阶系统也存在类似的关系。因为系统的频率特性与系统参数、结构之 间有着密切关系,所以可以利用研究频率特性的方法,把系统的参数、结 构变化和瞬态响应性能指标之间联系起来。 3) 频率特性有明确的物理意义,很多元件的这一特性都可以用实验的方法 确定,这对难于分析其物理规律来列出微分方程的元部件和系统,有很重 要的工程实际意义。 4) 频率特性分析法不仅适用于线性系统,而且可以推广到某些非线性系统。 5) 当系统在某些频率范围存在着严重噪声时,应用频率法,可以设计出能 够很好抑制这些噪声的系统
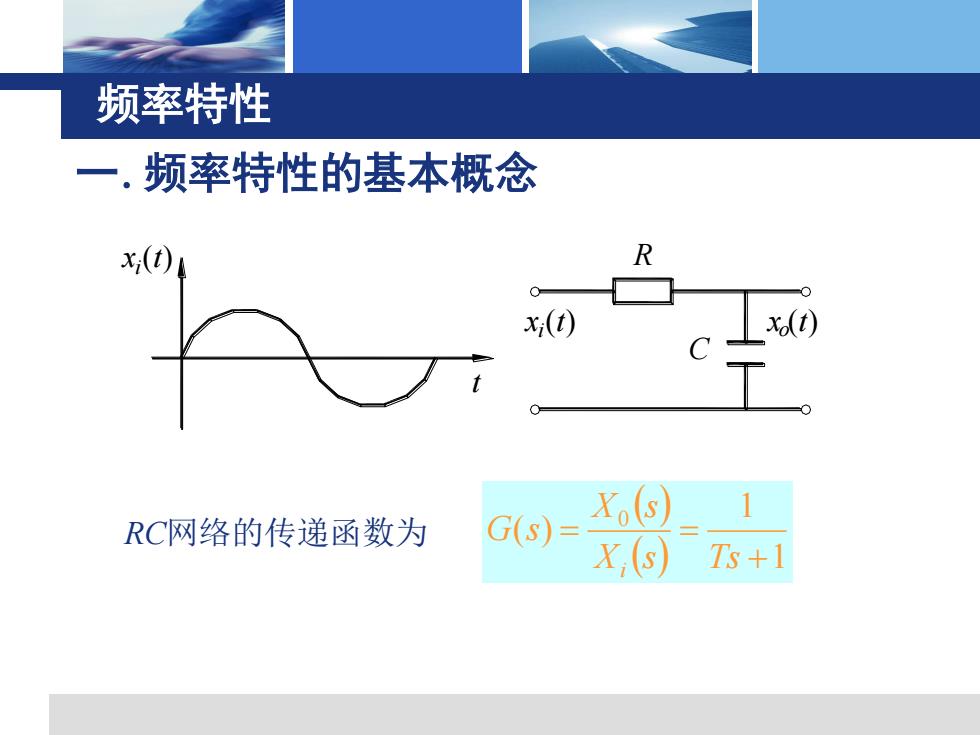
频率特性 一.频率特性的基本概念 x(t) R x;(t) x(t) XS) RC网络的传递函数为 G(S) X,(s Ts+1
频率特性 一.频率特性的基本概念 x (t) t C i R xi (t) xo(t) RC网络的传递函数为 ( ) ( ) 1 1 ( ) 0 + = = X s Ts X s G s i

输入信号 x,(t)=Asin ot 输出信号 x0) AoT A 1+o'Tze sin(@t-arctanoT) V1+02T2 系统稳态输出 i ()= 元nctan
输入信号 x (t) A t i = sin 输出信号 ( ) ( t T ) T A e T A T x t T t sin arctan 1 1 2 2 0 2 2 − + + + = − 系统稳态输出 ( ) ( t T ) T A x t t sin arctan 1 lim 2 2 0 − + = →

说明: 1.网络的稳态输出仍是弦电压其频率与输入电压相同 幅值是输入电压的yr。(幅频特性,相角比输入电压 滞后-arctgT@(相频特性). V1+T2@2 它描述了网络在正弦输作用下,稳态输出时电压幅值 和相角随正弦输入电题率0变化的规律称为网络的频 率特性 3. I+ioT TS+1 S-jo
TS 1 S j 1 1 j T 1 1 j T 1 j 1 jT -jarctg T 1 1 T 1 1 1 3. . , , 2. e e - arctgT ( ). ( ), 1. , , : (1 jT ) 1 2 2 2 2 + + = + + + + = = = + 率特性 和相角随正弦输入电压频 率 变化的规律 称为网络的 频 它描述了网络在正弦输入作用下 稳态输出时电压幅值 滞 后 相频特性 幅值是输入电压的 幅频特性 相角比输入电压 网络的稳态输出仍是正弦电压 其频率与输入电压相同 说 明 T
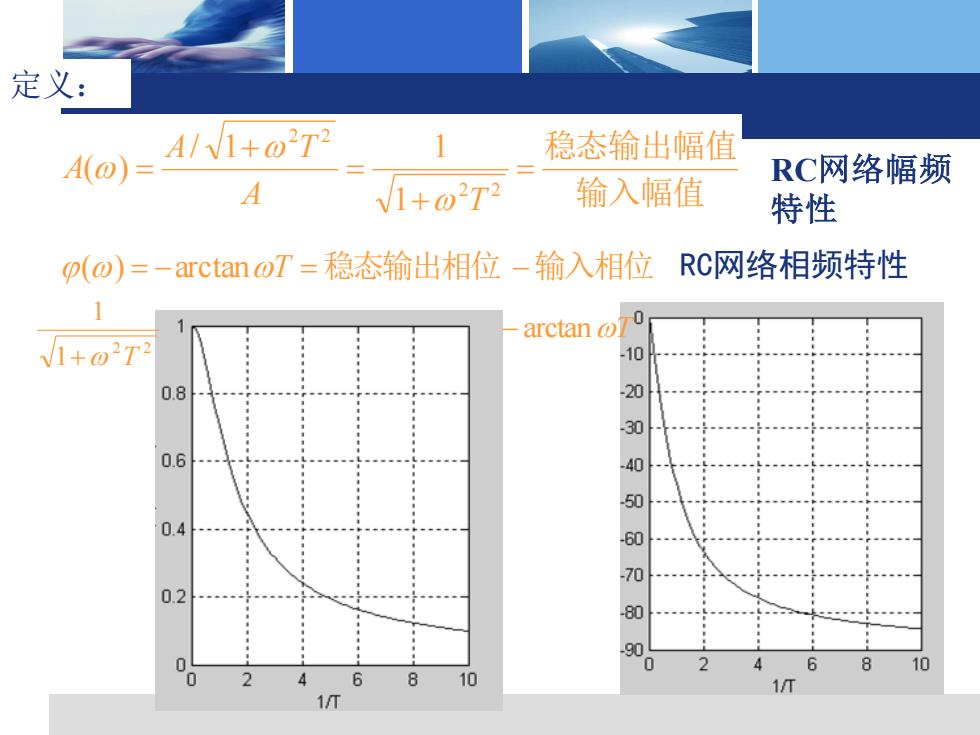
定义: A(o)= A/V1+02T2 稳态输出幅值 RC网络幅频 A V1+02T2 输入幅值 特性 p(o)=-arctan@T=稳态输出相位-输入相位 RC网络相频特性 1 arctan of 1+02T2 -10 0.8 20 0.6 0.4 040000 0.2 0 8 10 0 6 8 10 1/
定义: 输入幅值 稳态输出幅值 = + = + = 2 2 2 2 1 / 1 1 ( ) A T A T A RC网络幅频 特性 () = −arctan T = 稳态输出相位 −输入相位 RC网络相频特性 2 2 1 1 + T − arctan T

G(j0)= RCjo+11+jol 1 e/(-arctanoT) V1+02T2 A(@)ej) C电路的这一特性,对于任何稳定的线性网络都成立 虽然在前面的分析中,设定输入信号是正弦信号,然而频 率特性是系统的固有特性,与输入信号无关, 即当输入为非正弦信号时,系统仍然具有自身的频率特性
将s以j 代入RC网络传递函数,即得RC网络频率特性 RCj j T G j + = + = 1 1 1 1 ( ) ( arctan ) 2 2 1 1 j T e T − + = ( ) ( ) j = A e RC电路的这一特性,对于任何稳定的线性网络都成立 虽然在前面的分析中,设定输入信号是正弦信号,然而频 率特性是系统的固有特性,与输入信号无关, 即当输入为非正弦信号时,系统仍然具有自身的频率特性

频率特性定义为输出量的Fourier?变换与输入量 的Fourier?变换之比,即 G(w)-X.(o) X(io)
频率特性定义为输出量的Fourier变换与输入量 的Fourier变换之比,即 ( ) ( ) ( ) X j X j G j i 0 =

频率特性是一个复数,有三种表示: V(@) Gj) 代数式GUo)=U(o)+j(o) A(@) (@) 极坐标式 U()u G(Uo)=G(jo)∠G(jo)=Ao)∠p(o) 指数式 G(j@)=G(j@)ej2G()=A(@)e) A@)=G(j@)=JUP(@)+V2(@ U(@)=A@)cosp(@) V(o (@)=arctan V(@)=A(o)sino(@)
频率特性是一个复数,有三种表示: 代数式 G(j) =U() + jV() 极坐标式 ( ) ( ) ( ) ( ) ( ) j G j j G j = G j e = A e G( j) = G( j)G( j) = A()() 指数式 () ( ) () () 2 2 A = G j = U +V ( ) ( ) ( ) = U V arctan U() = A()cos() V() = A()sin() U() V() A() G(j) () u jv 0 频率特性的矢量图