
现代控制理论 一时域分析 Modern Control Theory
现代控制理论——时域分析 Modern Control Theory

控制象统的时域分杯法 绪言 典型输入信号 控制系统的时域性能指标 控制系统的稳定性和稳定判据 控制系统的稳态误差 控制系统暂态响应
控制系统的时域分析法 绪言 典型输入信号 控制系统的时域性能指标 控制系统的稳定性和稳定判据 控制系统的稳态误差 控制系统暂态响应

绪言 。 控制系统的分析方法 ·分析控制系统 ●第一步 建立模型 。第二步分析控制性能 。分析方法包括 ● 时域分析法 ●颇域分析法 ·根轨迹法
绪言 ⚫ 分析控制系统 ⚫ 第一步 建立模型 ⚫ 第二步 分析控制性能 ⚫ 分析方法包括 ⚫ 时域分析法 ⚫ 频域分析法 ⚫ 根轨迹法 一 . 控制系统的分析方法

线性系统的时域分析法 典型输入信号 线性定常系统的时域响应 控制系统的稳定性分析 线性系统的稳态误差计算 、二阶暂态响应性能指 高阶系统暂态响应分析
线性系统的时域分析法 典型输入信号 线性定常系统的时域响应 控制系统的稳定性分析 线性系统的稳态误差计算 一、二阶暂态响应性能指标 高阶系统暂态响应分析

典型输入信号Typical test signals ● 分析控制系统的第一步是建立模型,数学模型一旦建立,第二步分 析控制性能,分析有多种方法,主要有时域分析法,频域分析法,根 轨迹法等。 ●实际上,控制系统的输入信号常常是不知的,而是随机的。很难用解 析的方法表示。只有在一些特殊的情况下是预先知道的,可以用解析 的方法或者曲线表示。例如,切削机床的自动控制的例子。 ·在分析和设计控制系统时,对各种控制系统性能得有评判、比较的依 据。这个依据也许可以通过对这些系统加上各种输入信号,比较它们 对特定的输入信号的响应来建立。 ●许多设计准则就建立在这些信号的基础上,或者建立在系统对初始条 件变化(无任何试验信号)的基础上,因为系统对典型试验信号的响 应特性,与系统对实际输入信号的响应特性之间,存在着一定的关系; 所以采用试验信号即典型输入信号来评价系统性能是合理的
典型输入信号 Typical test signals ⚫ 分析控制系统的第一步是建立模型,数学模型一旦建立,第二步 分 析控制性能,分析有多种方法,主要有时域分析法,频域分析法,根 轨迹法等。 ⚫ 实际上,控制系统的输入信号常常是不知的,而是随机的。很难用解 析的方法表示。只有在一些特殊的情况下是预先知道的,可以用解析 的方法或者曲线表示。例如,切削机床的自动控制的例子。 ⚫ 在分析和设计控制系统时,对各种控制系统性能得有评判、比较的依 据。这个依据也许可以通过对这些系统加上各种输入信号,比较它们 对特定的输入信号的响应来建立。 ⚫ 许多设计准则就建立在这些信号的基础上,或者建立在系统对初始条 件变化(无任何试验信号)的基础上,因为系统对典型试验信号的响 应特性,与系统对实际输入信号的响应特性之间,存在着一定的关系; 所以采用试验信号即典型输入信号来评价系统性能是合理的

通常,给控制系统施加一定的输入信号,考察系统的输 出响应来分析系统性能。 常用的典型输入信号有阶跃函数、斜坡函数、抛物线函数、 脉冲函数和正弦函数。 一、阶跃函数 定义:式中A为常量。A=1的阶跃函数称为单位阶跃函数,记 为1(t)如式3-1所示。 A t≥0 r(t)= (3-1) 0 t<0
一、阶跃函数 通常,给控制系统施加一定的输入信号,考察系统的输 出响应来分析系统性能。 常用的典型输入信号有阶跃函数、斜坡函数、抛物线函数、 脉冲函数和正弦函数。 定义:式中A 为常量。A=1的阶跃函数称为单位阶跃函数,记 为1(t)如式3-1所示

单位阶跃函数的拉氏变换为: R6=10]=1 (3-2) 图3-1单位阶跃函数 通常运用阶跃函数作为典型输入作用信号,这样可在一 个统一的基础上对各种控制系统的特性进行比较和研究。本 章讨论系统对非周期信号(Step、Ramp)的相应;对正弦 试验信号相应,将在频域分析法,校正方法中讨论)
单位阶跃函数的拉氏变换为: 通常运用阶跃函数作为典型输入作用信号,这样可在一 个统一的基础上对各种控制系统的特性进行比较和研究。本 章讨论系统对非周期信号(Step、Ramp)的相应;对正弦 试验信号相应,将在频域分析法,校正方法中讨论)
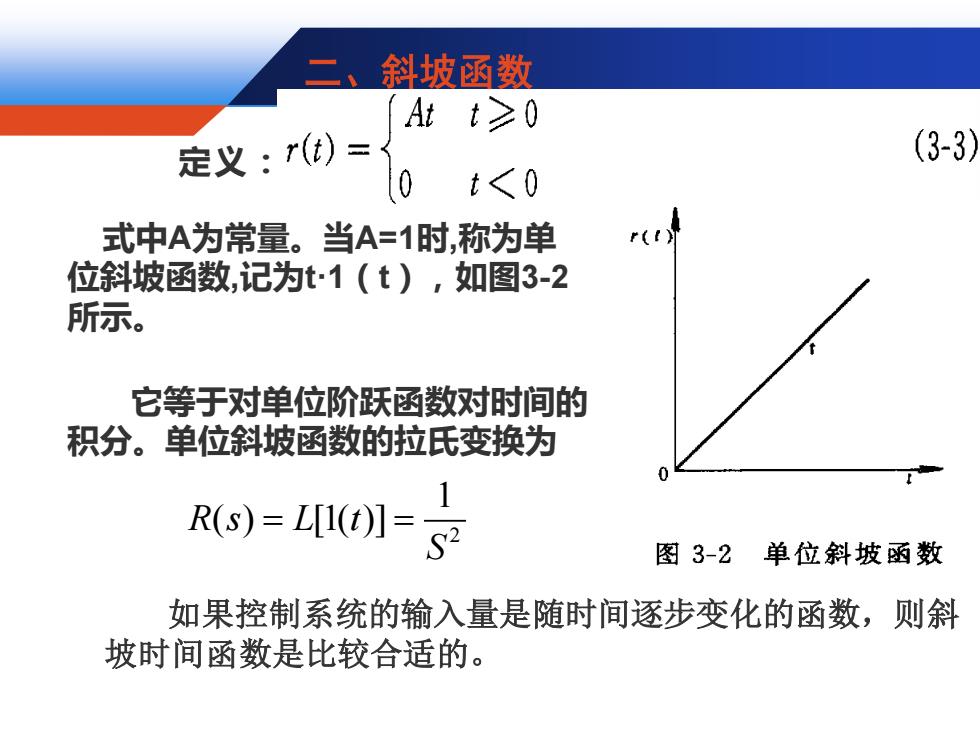
斜坡函数 Att≥0 定义:(t)= (3-3) 0 t<0 式中A为常量。当A=1时,称为单 r(t 位斜坡函数,记为t1(t),如图3-2 所示。 它等于对单位阶跃函数对时间的 积分。单位斜坡函数的拉氏变换为 1 R(s)=L[1(t)]= 图3-2单位斜坡函数 如果控制系统的输入量是随时间逐步变化的函数,则斜 坡时间函数是比较合适的
定义: 式中A为常量。当A=1时,称为单 位斜坡函数,记为t·1(t),如图3-2 所示。 它等于对单位阶跃函数对时间的 积分。单位斜坡函数的拉氏变换为 二、斜坡函数 如果控制系统的输入量是随时间逐步变化的函数,则斜 坡时间函数是比较合适的。 2 1 R s L t ( ) [1( )] S = =
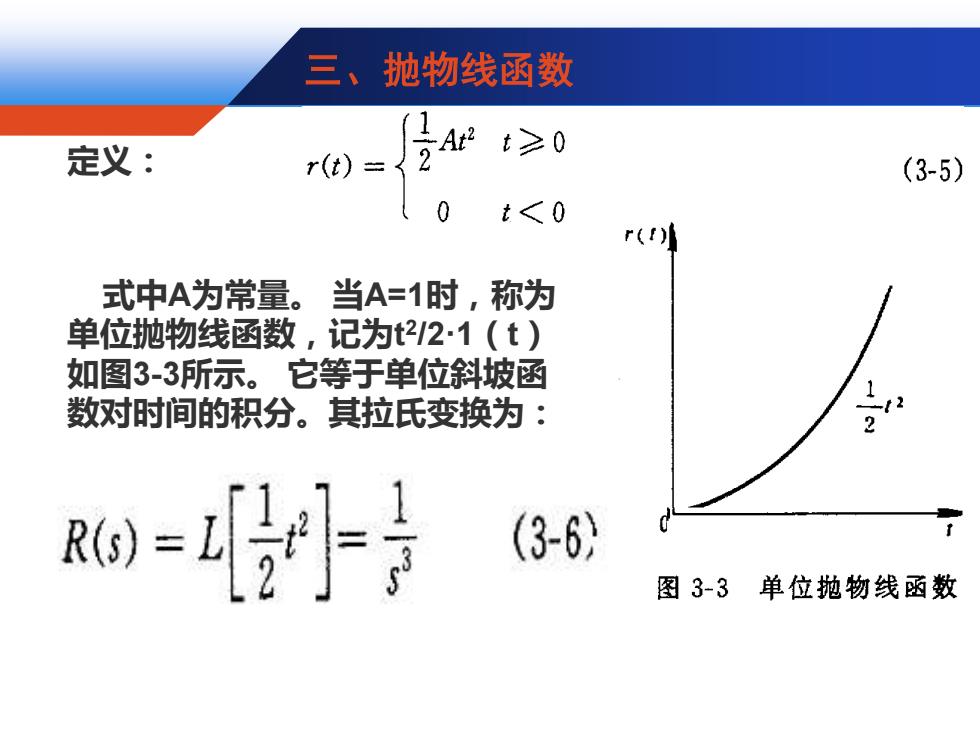
三、抛物线函数 定义: 2 t≥0 r(t)= (3-5) 0 t<0 式中A为常量。当A=1时,称为 单位抛物线函数,记为t221(t) 如图3-3所示。它等于单位斜坡函 数对时间的积分。其拉氏变换为: 2 0=剂月 (3-6) 图3-3单位抛物线函数
定义: 式中A为常量。 当A=1时,称为 单位抛物线函数,记为t 2 /2·1(t) 如图3-3所示。 它等于单位斜坡函 数对时间的积分。其拉氏变换为: 三、抛物线函数

四、脉冲函数 0e 脉冲函数如图3-4所示,令ε→0,则称为单位脉冲函数,记为 δ(t),见图3-4(b),有 6() 0 t=0 r(t)= (3-7) t主0 r(t)=1 (3-8) 单位脉冲函数的拉氏变换为: R(s)=L[6(t)]=1 (3-9) (b) 图3-4单位脉冲函数 单位脉冲函数是单位阶跃函数对 (a)>0时;(b)e=0时 时间的导数
定义为 : 脉冲函数如图3-4所示,令→0,则称为单位脉冲函数,记为 (t),见图3-4(b),有 单位脉冲函数的拉氏变换为: 单位脉冲函数是单位阶跃函数对 时间的导数, 四、脉冲函数