
机械动力学分析与设计 含弹性构件的机械系统动力学平面连杆机构
机械动力学分析与设计 含弹性构件的机械系统动力学—平面连杆机构

含弹性构件的机械系统动力学 构件弹性的影响: 1.产生振动、噪声; 2.附加动应力,引起构件疲劳破坏; 3.不能实现精确的运动规律或运动轨迹。 考虑构件弹性的场合: 1.构件重量减轻: 2.机械性能要求高 3.高速机械。 连杆机构 变形
含弹性构件的机械系统动力学 构件弹性的影响: 1. 产生振动、噪声; 2. 附加动应力,引起构件疲劳破坏; 3. 不能实现精确的运动规律或运动轨迹。 考虑构件弹性的场合: 1. 构件重量减轻; 2. 机械性能要求高; 3. 高速机械。 连杆机构 变形

一,构件弹性变形的类型 纵向变形 州 凸轮从动 件变形 横向变形 连杆机构 变形
一、构件弹性变形的类型 纵向变形 凸轮从动 件变形 横向变形 连杆机构 变形

一、构件弹性变形的类型 扭转变形 40A09 ④0A0R 传动轴 接触变形 齿轮传动
一、构件弹性变形的类型 扭转变形 传动轴 接触变形 齿轮传动

二,方程形式 拉氏方程 OF aU 中,势能 =Q, dt ad 6q,8q, 项不为零 r=1,2N 方程一般形式: 对离散系统及有 M阀+©+Kx-Q, 限元模型 用于离散系统的 传递矩阵形式 连续系统为二阶 偏微分方程
二、方程形式 r N Q q U q E q E dt d r r r r 1,2... ( ) . = = + − 拉氏方程 中,势能 项不为零 M x +Cx +Kx= Q 方程一般形式: 对离散系统及有 限元模型 用于离散系统的 传递矩阵形式 连续系统为二阶 偏微分方程

三,求解方法 直接积分法 解析解 数值解 振形分析法 可得出有确切物 理意义的结果 解析解 数值解
三、求解方法 直接积分法 解析解 数值解 振形分析法 可得出有确切物 理意义的结果 解析解 数值解
四、建模方法 建模方法 刚弹性模型 Kineto- Elastodynamics 多柔体动力学 模型
建模方法 刚弹性模型 Kineto- Elastodynamics 多柔体动力学 模型 四、建模方法
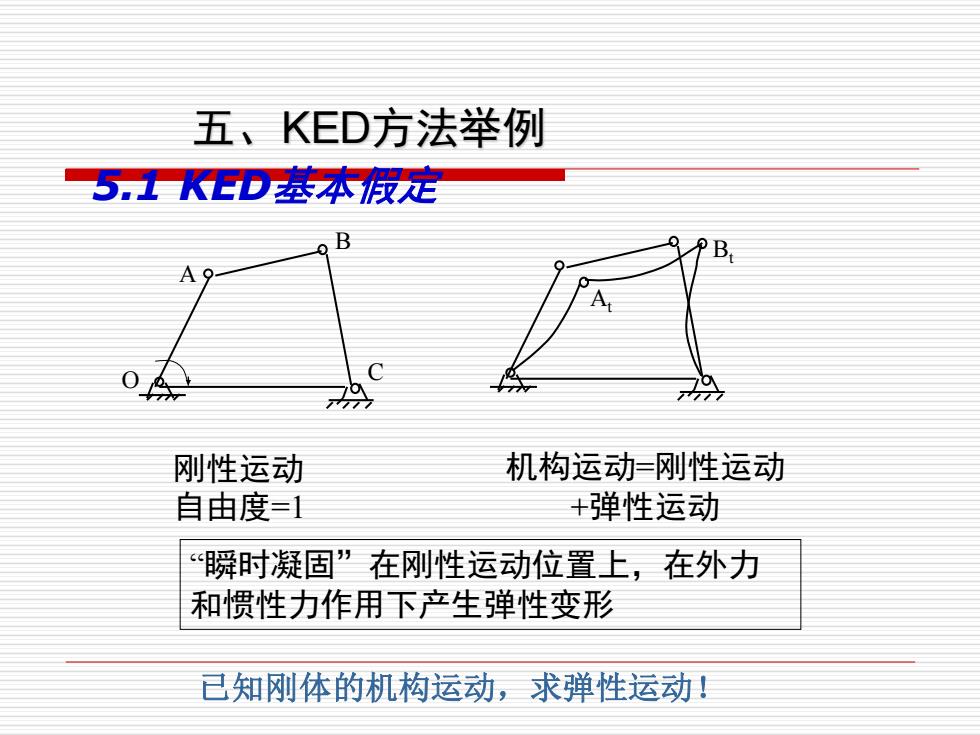
五、KED方法举例 5.1KED基本假定 B B 70 刚性运动 机构运动=刚性运动 自由度=1 +弹性运动 瞬时凝固”在刚性运动位置上,在外力 和惯性力作用下产生弹性变形 已知刚体的机构运动,求弹性运动
5.1 KED基本假定 “瞬时凝固”在刚性运动位置上,在外力 和惯性力作用下产生弹性变形 刚性运动 自由度=1 A B O C 机构运动=刚性运动 +弹性运动 At Bt 五、KED方法举例 已知刚体的机构运动,求弹性运动!

5.2分析方法 离散模型一传递矩阵法 振型分析法 有限元模型 用有限元法分析 机构弹性运动
5.2 分析方法 用有限元法分析 机构弹性运动 离散模型—传递矩阵法 振型分析法 有限元模型

5.3单元划分 节点 一维单元 单元: 二维单元 四杆机构 三角形单元 单元2 单元3 单元1 三维单元 ■■■■
5.3 单元划分 一维单元 单元: 1 2……. 节点 1 2……... 二维单元 三角形单元 . . . . 三维单元 . . . . . 单元1 单元2 单元3 四杆机构