
典型相关分析
1 典型相关分析

要点 ■典型相关分析的数学表达方式,假定条件: ■典型相关系数的数学含义; ■典型变量系数的数学含义; ■简单相关,复相关和典型相关的意义; ■典型相关的应用 2
2 要 点 典型相关分析的数学表达方式,假定条件; 典型相关系数的数学含义; 典型变量系数的数学含义; 简单相关,复相关和典型相关的意义; 典型相关的应用

一、什么是典型相关分析及基本思想 通常情况下,为了研究两组变量 (X1,X2,.,xp) (,y2,.,yg) 的相关关系,可以用最原始的方法,分别计 算两组变量之间的全部相关系数,一共有Dq 个简单相关系数,这样又烦琐又不能抓住问 题的本质。如果能够采用类似于主成分的思 想,分别找出两组变量的各自的某个线性组 合,讨论线性组合之间的相关关系,则更简 捷。 3
3 一、什么是典型相关分析及基本思想 通常情况下,为了研究两组变量 的相关关系,可以用最原始的方法,分别计 算两组变量之间的全部相关系数,一共有pq 个简单相关系数,这样又烦琐又不能抓住问 题的本质。如果能够采用类似于主成分的思 想,分别找出两组变量的各自的某个线性组 合,讨论线性组合之间的相关关系,则更简 捷。 ),( 21 p x x L x ),( 21 q y y L y

在解决实际问题中,这种方法有广泛的应 用。如,在工厂里常常要研究产品的q个质量指 标(,2,.,y)和P个原材料的指标(:,x2,.,x) 之间的相关关系;也可以是采用典型相关分析 来解决的问题。如果能够采用类似于主成分的 思想,分别找出两组变量的线性组合既可以使 变量个数简化,又可以达到分析相关性的目 的
4 在解决实际问题中,这种方法有广泛的应 用。如,在工厂里常常要研究产品的q个质量指 标 和P个原材料的指标 之间的相关关系;也可以是采用典型相关分析 来解决的问题。如果能够采用类似于主成分的 思想,分别找出两组变量的线性组合既可以使 变量个数简化,又可以达到分析相关性的目 的。 ),( 21 p ),( x x L x 21 q y y L y

例家庭特征与家庭消费之间的关系 为了了解家庭的特征与其消费模式之间的关系。 调查了70个家庭的下面两组变量: :户主的年龄 X灯 每年去餐馆就餐的频率 y2: 家庭的年收入 x2: 每年外出看电影频率 :户主受教育程度 分析两组变量之间的关系。 5
5 例 家庭特征与家庭消费之间的关系 为了了解家庭的特征与其消费模式之间的关系。 调查了70个家庭的下面两组变量: ⎪ ⎩ ⎪ ⎨ ⎧ :户主受教育程度 :家庭的年收入 :户主的年龄 3 2 1 y y y ⎩ ⎨ ⎧ :每年外出看电影频率 :每年去餐馆就餐的频 率 2 1 x x 分析两组变量之间的关系

变量间的相关系数矩阵 X1 X2 y1 y2 y3 X1 1.00 0.80 0.26 0.67 0.34 X2 0.80 1.00 0.33 0.59 0.34 y1 0.26 0.33 1.00 0.37 0.21 y2 0.67 0.59 0.37 1.00 0.35 y3 0.34 0.34 0.21 0.35 1.00 6
6 X1 X2 y1 y2 y3 X1 1.00 0.80 0.26 0.67 0.34 X2 0.80 1.00 0.33 0.59 0.34 y1 0.26 0.33 1.00 0.37 0.21 y2 0.67 0.59 0.37 1.00 0.35 y3 0.34 0.34 0.21 0.35 1.00 变量间的相关系数矩阵
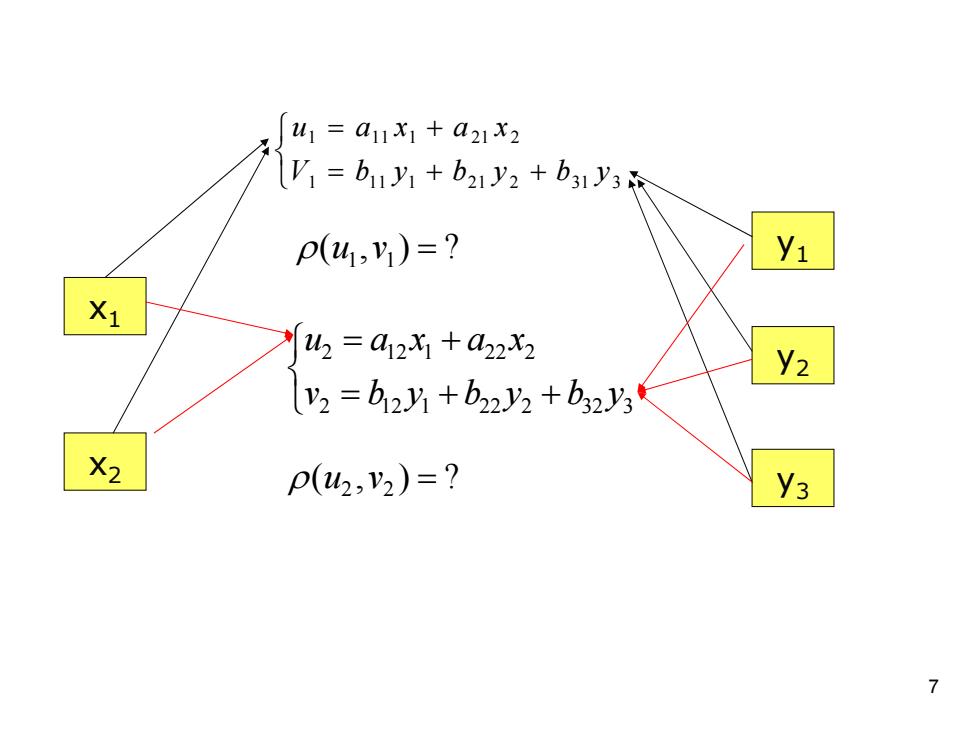
41=a11X1+a21X2 y1=b1y1+b21y2+b31y3 p(41,y)=? X1 W2=412x1+22X2 y2=b12+b22y2+b2y3 X2 p(2,V2)=? y3 1
7 y2 y3 y1 x2 x1 ⎩⎨⎧ ++== + 3312211111 2211111 ybybybV xaxau ⎩⎨⎧ ++== + 3322221122 2221122 ybybybv xaxau ?),( ρ vu 11 = ?),( ρ vu 22 =

典型相关分析的思想: 首先分别在每组变量中找出第一对线性组 合,使其具有最大相关性, u1=ax1+a21x2+.+apixp v=buy+62192+.+bqiya 8
8 典型相关分析的思想: 首先分别在每组变量中找出第一对线性组 合,使其具有最大相关性, 1 11 1 21 2 1 1 11 1 21 2 1 p p q q u ax ax a x v by by by ⎧ = + ++ ⎪ ⎨ ⎪ = + ++ ⎩ L L

然后再在每组变量中找出第二对线性组 合,使其分别与本组内的第一线性组合不相 关,第二对本身具有次大的相关性。 u =a2+az2+.+ap2xp y2=b2y+b2y2+.+b2yg U2和V2与u1和V1相互独立,但u2和V2相关。如 此继续下去,直至进行到步,两组变量的相关性 被提取完为止。r≤min(p,q),可以得到r组变量
9 然后再在每组变量中找出第二对线性组 合,使其分别与本组内的第一线性组合不相 关,第二对本身具有次大的相关性。 u 2 和 v 2 与 u 1 和 v 1相互独立,但 u 2 和 v 2相关。如 此继续下去,直至进行到 r步,两组变量的相关性 被提取完为止。 r ≤min(p,q),可以得到 r组变量。 2 12 1 22 2 2 2 12 1 22 2 2 p p q q u ax ax a x v b y b y b y ⎧ = + ++ ⎪ ⎨ ⎪ = + ++ ⎩ L L

例家庭特征与家庭消费之间的关系 为了了解家庭的特征与其消费模式之间的关系。 调查了70个家庭的下面两组变量: :户主的年龄 x:每年去餐馆就餐的频率 V2: 家庭的年收入 x2: 每年外出看电影频率 :户主受教育程度 分析两组变量之间的关系。 10
10 例 家庭特征与家庭消费之间的关系 为了了解家庭的特征与其消费模式之间的关系。 调查了70个家庭的下面两组变量: ⎪ ⎩ ⎪ ⎨ ⎧ :户主受教育程度 :家庭的年收入 :户主的年龄 3 2 1 y y y ⎩ ⎨ ⎧ :每年外出看电影频率 :每年去餐馆就餐的频 率 2 1 x x 分析两组变量之间的关系