
主成分分析与因子分析 介绍: 1、主成分分析与因子分析的概念 2、主成分分析与因子分析的过程
主成分分析与因子分析 介绍: 1、主成分分析与因子分析的概念 2、主成分分析与因子分析的过程

主成分分析与因子分析的概念 需要与可能:在各个领域的科学研究中,往往需要对反映事物的多 个变量进行大量的观测,收集大量数据以便进行分析寻找规律。多 变量大样本无疑会为科学研究提供丰富的信息,但也在一定程度上 增加了数据采集的工作量,更重要的是在大多数情况下,许多变量 之间可能存在相关性而增加了问题分析的复杂性,同时对分析带来 不便。如果分别分析每个指标,分析又可能是孤立的,而不是综合 的。盲目减少指标会损失很多信息,容易产生错误的结论。因此需 要找到一个合理的方法,减少分析指标的同时,尽量减少原指标包 含信息的损失,对所收集的资料作全面的分析。由于各变量间存在 一定的相关关系,因此有可能用较少的综合指标分别综合存在于各 变量中的各类信息。主成分分析与因子分析就是这样一种降维的方 法。 ●主成分分析与因子分析是将多个实测变量转换为少数几个不相关的 综合指标的多元统计分析方法 直线综合指标往往是不能直接观测到的,但它更能反映事物的本质。 因此在医学、心理学、经济学等科学领域以及社会化生产中得到广 泛的应用
主成分分析与因子分析的概念 需要与可能:在各个领域的科学研究中,往往需要对反映事物的多 个变量进行大量的观测,收集大量数据以便进行分析寻找规律。多 变量大样本无疑会为科学研究提供丰富的信息,但也在一定程度上 增加了数据采集的工作量,更重要的是在大多数情况下,许多变量 之间可能存在相关性而增加了问题分析的复杂性,同时对分析带来 不便。如果分别分析每个指标,分析又可能是孤立的,而不是综合 的。盲目减少指标会损失很多信息,容易产生错误的结论。因此需 要找到一个合理的方法,减少分析指标的同时,尽量减少原指标包 含信息的损失,对所收集的资料作全面的分析。由于各变量间存在 一定的相关关系,因此有可能用较少的综合指标分别综合存在于各 变量中的各类信息。主成分分析与因子分析就是这样一种降维的方 法。 主成分分析与因子分析是将多个实测变量转换为少数几个不相关的 综合指标的多元统计分析方法 直线综合指标往往是不能直接观测到的,但它更能反映事物的本质。 因此在医学、心理学、经济学等科学领域以及社会化生产中得到广 泛的应用

主成分分析与因子分析的概念(续)〉 ◆由于实测的变量间存在一定的相关关系, 因此有可能用较少数的综合指标分别综合 存在于各变量中的各类信息,而综合指标 之间彼此不相关,即各指标代表的信息不 重叠。综合指标称为因子或主成分(提取 几个因子),一般有两种方法: ◆特征值>1 ◆累计贡献率>0.8
主成分分析与因子分析的概念(续) 由于实测的变量间存在一定的相关关系, 因此有可能用较少数的综合指标分别综合 存在于各变量中的各类信息,而综合指标 之间彼此不相关,即各指标代表的信息不 重叠。综合指标称为因子或主成分(提取 几个因子),一般有两种方法: 特征值>1 累计贡献率>0.8

主成分分析 ◆每个人都会遇到有很多变量的数据。 ◆比如全国或各个地区的带有许多经济和社会变 量的数据;各个学校的研究、教学等各种变量 的数据等等。 愈这些数据的共同特点是变量很多,在如此多的 变量之中,有很多是相关的。人们希望能够找 出它们的少数“代表”来对它们进行描述。 ◆本章就介绍两种把变量维数降低以便于描述、 理解和分析的方法:主成分分析(principal component analysis)和因子分析(factor analysis)。实际上主成分分析可以说是因子 分析的一个特例。在引进主成分分析之前,先 看下面的例子
主成分分析 每个人都会遇到有很多变量的数据。 比如全国或各个地区的带有许多经济和社会变 量的数据;各个学校的研究、教学等各种变量 的数据等等。 这些数据的共同特点是变量很多,在如此多的 变量之中,有很多是相关的。人们希望能够找 出它们的少数 “代表 ”来对它们进行描述。 本章就介绍两种把变量维数降低以便于描述、 理解和分析的方法:主成分分析(principal component analysis ) 和 因子分析 ( factor analysis)。实际上主成分分析可以说是因子 分析的一个特例。在引进主成分分析之前,先 看下面的例子
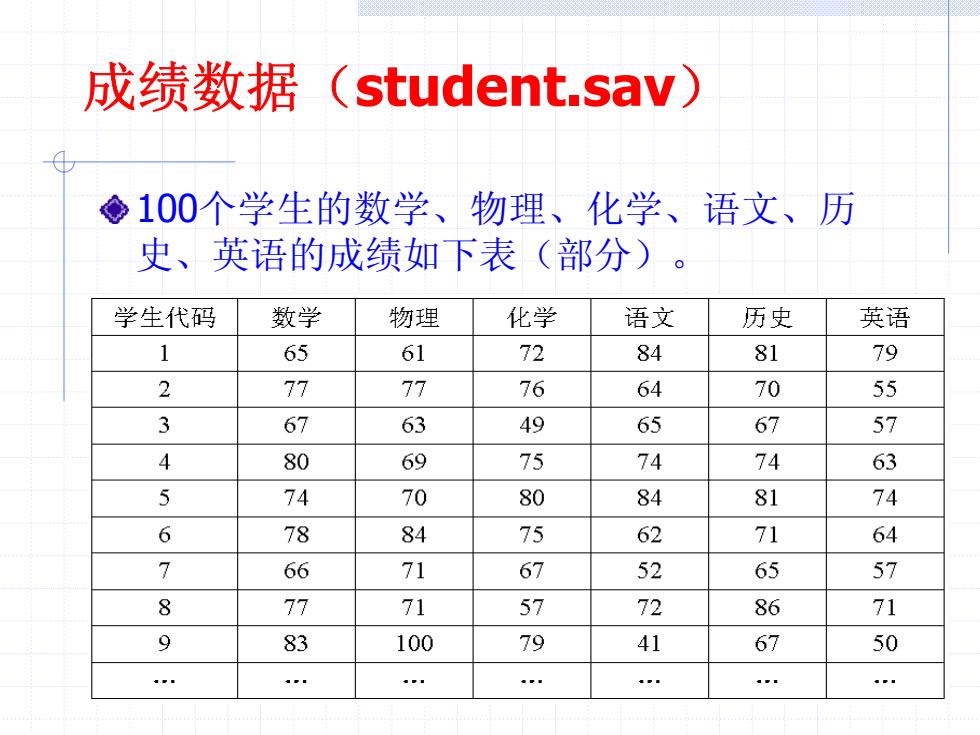
成绩数据(student.sav) ◆100个学生的数学、物理、化学、语文、历 史、英语的成绩如下表(部分)。 学生代码 数学 物理 化学 语文 历史 英语 1 65 61 72 84 81 79 2 77 77 76 64 70 55 3 67 63 49 65 67 57 4 80 69 75 74 74 63 5 74 70 80 84 81 74 6 78 84 75 62 71 64 7 66 71 67 52 65 57 8 77 71 57 72 86 71 9 83 100 79 41 67 50
成绩数据(student.sav) 100个学生的数学、物理、化学、语文、历 史、英语的成绩如下表(部分)

从本例可能提出的问题 ◆目前的问题是,能不能把这个数据的6 个变量用一两个综合变量来表示呢? ◆这一两个综合变量包含有多少原来的信 息呢? ◆能不能利用找到的综合变量来对学生排 序呢?这一类数据所涉及的问题可以推 广到对企业,对学校进行分析、排序、 判别和分类等问题
从本例可能提出的问题 目前的问题是,能不能把这个数据的6 个变量用一两个综合变量来表示呢? 这一两个综合变量包含有多少原来的信 息呢? 能不能利用找到的综合变量来对学生排 序呢?这一类数据所涉及的问题可以推 广到对企业,对学校进行分析、排序、 判别和分类等问题

主成分分 ◆例中的的数据点是六维的;也就是说,每个观 测值是6维空间中的一个点。我们希望把6维空 间用低维空间表示。 ◆先假定只有二维,即只有两个变量,它们由横 坐标和纵坐标所代表;因此每个观测值都有相 应于这两个坐标轴的两个坐标值;如果这些数 据形成一个椭圆形状的点阵(这在变量的二维 正态的假定下是可能的) ◆那么这个椭圆有一个长轴和一个短轴。在短轴 方向上,数据变化很少;在极端的情况,短轴 如果退化成一点,那只有在长轴的方向才能够 解释这些点的变化了;这样,由二维到一维的 降维就自然完成了
主成分分析 例中的的数据点是六维的;也就是说,每个观 测值是 6维空间中的一个点。我们希望把 6维空 间用低维空间表示。 先假定只有二维,即只有两个变量,它们由横 坐标和纵坐标所代表;因此每个观测值都有相 应于这两个坐标轴的两个坐标值;如果这些数 据形成一个椭圆形状的点阵(这在变量的二维 正态的假定下是可能的) 那么这个椭圆有一个长轴和一个短轴。在短轴 方向上,数据变化很少;在极端的情况,短轴 如果退化成一点,那只有在长轴的方向才能够 解释这些点的变化了;这样,由二维到一维的 降维就自然完成了

主成分分析 ◆当坐标轴和椭圆的长短轴平行,那么代表 长轴的变量就描述了数据的主要变化,而 代表短轴的变量就描述了数据的次要变化。 ◆但是,坐标轴通常并不和椭圆的长短轴平 行。因此,需要寻找椭圆的长短轴,并进 行变换,使得新变量和椭圆的长短轴平行。 ◆如果长轴变量代表了数据包含的大部分信 息,就用该变量代替原先的两个变量(舍 去次要的一维),降维就完成了。 ◆ 椭圆(球)的长短轴相差得越大,降维也 越有道理
主成分分析 当坐标轴和椭圆的长短轴平行,那么代表 长轴的变量就描述了数据的主要变化,而 代表短轴的变量就描述了数据的次要变化。 但是,坐标轴通常并不和椭圆的长短轴平 行。因此,需要寻找椭圆的长短轴,并进 行变换,使得新变量和椭圆的长短轴平行。 如果长轴变量代表了数据包含的大部分信 息,就用该变量代替原先的两个变量(舍 去次要的一维),降维就完成了。 椭圆(球)的长短轴相差得越大,降维也 越有道理

00 含秦
- 4 - 2 0 2 4 -4 -2 0 2 4

主成分分析 ◆对于多维变量的情况和二维类似,也 有高维的椭球,只不过无法直观地看 见罢了。 ◆首先把高维椭球的主轴找出来,再用 代表大多数数据信息的最长的几个轴 作为新变量;这样,主成分分析就基 本完成了。 ◆注意,和二维情况类似,高维椭球的 主轴也是互相垂直的。这些互相正交 的新变量是原先变量的线性组合,叫 做主成分(principal component)
主成分分析 对于多维变量的情况和二维类似,也 有高维的椭球,只不过无法直观地看 见罢了。 首先把高维椭球的主轴找出来,再用 代表大多数数据信息的最长的几个轴 作为新变量;这样,主成分分析就基 本完成了。 注意,和二维情况类似,高维椭球的 主轴也是互相垂直的。这些互相正交 的新变量是原先变量的线性组合,叫 做主成分(principal component)