
第2章地理数据与处理 地理数据,是对地理问颗进行定量化描述和研究的基础,是计量地理学研究与应用的 先决条件。所谓地理数据,就是用一定的测度方式描述和衡量地理对象的又量化标志。对于 不同的地理实体、地理要素、地理现象、地理事件、地理过程,需要采用不同的测度方式 测度标准进行描述和衡量,这样就产生了不同类型的地理数据。不同类型的地理数据,反映 者不同类型的地理问题。对于不同类型的地理数据,常常需要采用不同的方法。 第1节地理数据的类型 地理学的研究对象一地理系统,总是与一定的地理区域相对应的。任何地理实体、地 理要素、地理现象、地理事件、地理过程、其产生和发展都离不开具体的地理位置和地域空 间范围。因此,我们可以将所有的地理数据划分为两大基木类型,即空间数据和属性数据。 2.1.1空间数据 空间数据,用干描述地理实体、地理要素、地理现象、恤理电件及地理过程产生、存 在和发展的地理位置 区域范围及空间联系。对于空间数据的表达,可以将其归纳为点、线 面三种几何实体以及描述他们之间空间联系的拓扑关系。其中 (一)点由一个独立的坐标点(x,y)定位,是空间上不可再分的几何实体。它可 以表示精确的地理位置点,也可以是一些地理实体的抽象。 (一)线由若个(至少两个,理论上是无穷个)华标占(x,v)(1=1,2,) 定义,有一定的长度和走向,表示线状地物或点实体之间的联系 交通线、 可流 (三)面表示在空间上连续分布的地理景观或区域。譬如,某种土壤或植被的分布区 点、线、面是三种地理几何实体,按照一定的拓扑关系组合、排列,就可以形成更为 复杂的地理几何实体。譬如,点、线形成我那个罗:线面组合形成地带:点、面组合形成地 域类型:点、线、面组合形成地理区。点、线、面三种几何实体及其组合关系可以形象地用 图211表示。 点 网络 地域类型 区域 线 面 地指 图2.11三种基本的地理几何实体及其组合 2.12属性数据 属性数据,用于描述地理实体、地理要素、地理现象、地理事件、地理过程的有关属性
第 2 章 地理数据与处理 地理数据,是对地理问题进行定量化描述和研究的基础,是计量地理学研究与应用的 先决条件。所谓地理数据,就是用一定的测度方式描述和衡量地理对象的又量化标志。对于 不同的地理实体、地理要素、地理现象、地理事件、地理过程,需要采用不同的测度方式和 测度标准进行描述和衡量,这样就产生了不同类型的地理数据。不同类型的地理数据,反映 着不同类型的地理问题。对于不同类型的地理数据,常常需要采用不同的方法。 第 1 节 地理数据的类型 地理学的研究对象-地理系统,总是与一定的地理区域相对应的。任何地理实体、地 理要素、地理现象、地理事件、地理过程、其产生和发展都离不开具体的地理位置和地域空 间范围。因此,我们可以将所有的地理数据划分为两大基本类型,即空间数据和属性数据。 2.1.1 空间数据 空间数据,用于描述地理实体、地理要素、地理现象、地理事件及地理过程产生、存 在和发展的地理位置、区域范围及空间联系。对于空间数据的表达,可以将其归纳为点、线、 面三种几何实体以及描述他们之间空间联系的拓扑关系。其中 (一)点 由一个独立的坐标点(x,y)定位,是空间上不可再分的几何实体 。它可 以表示精确的地理位置点,也可以是一些地理实体的抽象。 (二)线 由若干个(至少两个,理论上是无穷个)坐标点(xi,yi)(i =1,2,.) 定义,有一定的长度和走向,表示线状地物或点实体之间的联系。 譬如,交通线、河流 (三)面 表示在空间上连续分布的地理景观或区域。譬如,某种土壤或植被的分布区。 点、线、面是三种地理几何实体,按照一定的拓扑关系组合、排列,就可以形成更为 复杂的地理几何实体。譬如,点、线形成我那个罗;线面组合形成地带;点、面组合形成地 域类型;点、线、面组合形成地理区。点、线、面三种几何实体及其组合关系可以形象地用 图 2.1.1 表示。 网络 地域类型 地带 区域 线 点 面 图 2.1.1 三种基本的地理几何实体及其组合 2.1.2 属性数据 属性数据,用于描述地理实体、地理要素、地理现象、地理事件、地理过程的有关属性
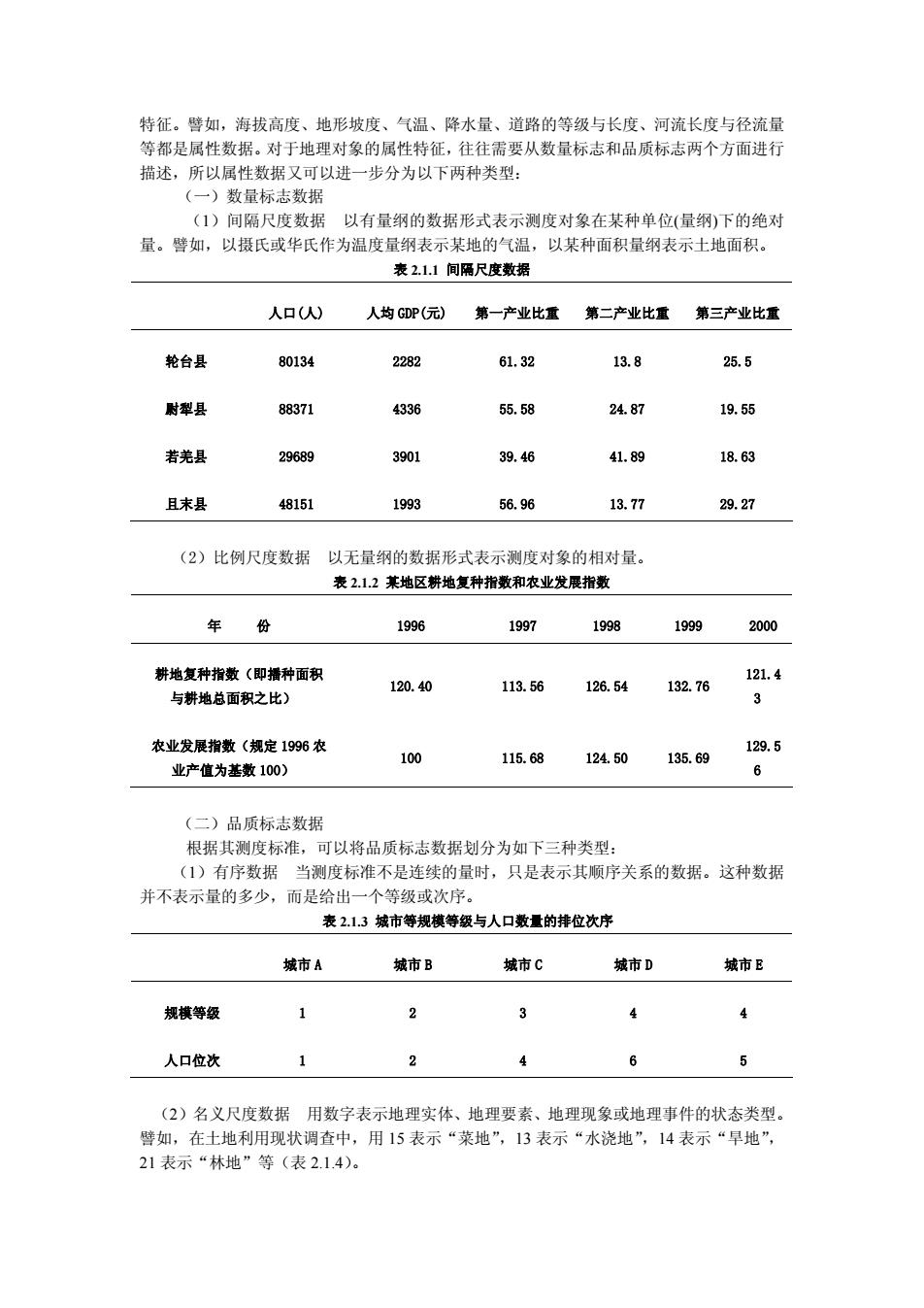
特征。譬如,海拔高度、地形坡度、气温、降水量、道路的等级与长度、河流长度与径流量 等都是属性数据。对于地理对象的属性特征,往往需要从数量标志和品质标志两个方面进行 描述,所以属性数据又可以进一步分为以下两种类型: 数量标志数 (1)间隔尺度数据以有量纲的数据形式表示测度对象在某种单位(量纲)下的绝对 量。譬如,以摄氏或华氏作为温度量纲表示某地的气温,以某种面积量纲表示土地面积。 表2.1.1间隔尺度数据 人口) 人均GDP(元)第一产业比重第二产业比重第三产业比重 轮台县 80134 2282 61.32 13.8 25.5 尉犁县 88371 4336 55.58 24.87 19.55 若光县 29689 3901 39.46 41.89 18.63 且末县 48151 193 56.96 13.77 29.27 (2)比例尺度数据以无量纲的数据形式表示测度对象的相对量。 表2.12某地区耕地复种指数和农业发限指数 年份 1996 1997 1998 1999 2000 耕地复种指数(即措种面积 120.40 113.56 126.54 132.76 121.4 与耕地总面积之比) 3 农业发展指数(规定1996农 129.5 100 业产值为基数100) 115.6812450135.69 6 (二)品质标志数据 根据其测度标准,以将品质标志数据别分为加下二种类型: (1)有序数据 当测度标准不是连续的量时,只是表示其顺序关系的数据。这种数据 并不表示量的多少,而是给出一个等级或次序。 表21.3城市等规模等级与人口数量的排位次序 城市A 城市B 城市C城市D 城市B 规棋等级 1 2 3 4 4 人口位次 1 2 4 6 5 (2)名义尺度数据用数字表示地理实体、地理要素、地理现象或地理事件的状态类型 譬如,在士地利用现状调查中 ,用15表示“莱地”,13表示“水浇地”,14表示“旱地” 21表示“林地”等(表2.1.4)
特征。譬如,海拔高度、地形坡度、气温、降水量、道路的等级与长度、河流长度与径流量 等都是属性数据。对于地理对象的属性特征,往往需要从数量标志和品质标志两个方面进行 描述,所以属性数据又可以进一步分为以下两种类型: (一)数量标志数据 (1)间隔尺度数据 以有量纲的数据形式表示测度对象在某种单位(量纲)下的绝对 量。譬如,以摄氏或华氏作为温度量纲表示某地的气温,以某种面积量纲表示土地面积。 表 2.1.1 间隔尺度数据 人口(人) 人均 GDP(元) 第一产业比重 第二产业比重 第三产业比重 轮台县 80134 2282 61.32 13.8 25.5 尉犁县 88371 4336 55.58 24.87 19.55 若羌县 29689 3901 39.46 41.89 18.63 且末县 48151 1993 56.96 13.77 29.27 (2)比例尺度数据 以无量纲的数据形式表示测度对象的相对量。 表 2.1.2 某地区耕地复种指数和农业发展指数 年 份 1996 1997 1998 1999 2000 耕地复种指数(即播种面积 与耕地总面积之比) 120.40 113.56 126.54 132.76 121.4 3 农业发展指数(规定 1996 农 业产值为基数 100) 100 115.68 124.50 135.69 129.5 6 (二)品质标志数据 根据其测度标准,可以将品质标志数据划分为如下三种类型: (1)有序数据 当测度标准不是连续的量时,只是表示其顺序关系的数据。这种数据 并不表示量的多少,而是给出一个等级或次序。 表 2.1.3 城市等规模等级与人口数量的排位次序 城市 A 城市 B 城市 C 城市 D 城市 E 规模等级 1 2 3 4 4 人口位次 1 2 4 6 5 (2)名义尺度数据 用数字表示地理实体、地理要素、地理现象或地理事件的状态类型。 譬如,在土地利用现状调查中,用 15 表示“菜地”,13 表示“水浇地”,14 表示“旱地”, 21 表示“林地”等(表 2.1.4)

(3)二元数据用0、1两个数据表示地理事物、地理现象或地理事件的是非判断问题。 譬如,在人口统计中,用1表示男性,用0表示女性,在一个交通网络中,两两组合考虑结 点之间有无连线的情况,1表示“两个结点之间存在连线”,0表示“两个结点之不存在连 线”等表2.1.5)。 表2.1.4土地利用类型 地块序列号 1 2 3 4 5 6 土地利用类型 13 15 21 14 14 31 表2.15二元数(1表示两城市之间通航,0表示两城市之间不通航) 城市A 城市B 城市C 城市D 城市E 城市A 1 1 城市B 1 0 城市C 1 1 1 0 城市D 0 城市E 1 0 0 第2节地理数据的基本特征 地理系统的复杂性决定了地理数据的复杂性和多样性。对于不同的地理实体、地理要 素、地理现象、地理事件,地理过程,需要采用不同的数据形式和数据类型进行描述。对于 一个地理区域,则盂要从冬种角度,采用不同的数据形式和数展类型,对甘冬个方面的性质 分别进行描述。尽管地理数据的种类是多样的,数据的信息是海量的,但是一般而言,所有 的地理数据就都具有如下的几个方面的基本特征: 2.2.1数量化、形式化与逻辑化 (一)形式化、逻辑化与数量化,是所有地理数据的共同特征。 (二)定量化的地理数据是建立地理数学模型的基础,它有两方面的作用: (1)确定模型的参数、给定模型运行的初值条件:(2)检验模型的有效性。 (三)地理计算学,对于地理数据的形式化、逻辑化提出了更高的要求,要求“整体“和 “大容量“的地理数据具有统一的数据形式和交换标准。 地理计算学,对于地理数据的形式化、逻辑化提出了更高的要求,要求“整体”和“大 容量”的地理数据具有同一的数据形式和交换标准,从而使统一数据能够在不同的计算过程 中被使用:要求各种地理数据之间具有合理的逻辑关系,从而保证模型系统的运行剁成及计 算结果的正确性
(3)二元数据 用 0、1 两个数据表示地理事物、地理现象或地理事件的是非判断问题。 譬如,在人口统计中,用 1 表示男性,用 0 表示女性,在一个交通网络中,两两组合考虑结 点之间有无连线的情况,1 表示“两个结点之间存在连线”,0 表示“两个结点之间不存在连 线”等(表 2.1.5)。 表 2.1.4 土地利用类型 地块序列号 1 2 3 4 5 6 土地利用类型 13 15 21 14 14 31 表 2.1.5 二元数(1 表示两城市之间通航,0 表示两城市之间不通航) 城市 A 城市 B 城市 C 城市 D 城市 E 城市 A — 1 1 0 1 城市 B 1 — 1 1 0 城市 C 1 1 — 1 0 城市 D 0 1 1 — 1 城市 E 1 0 0 1 — 第 2 节 地理数据的基本特征 地理系统的复杂性决定了地理数据的复杂性和多样性。对于不同的地理实体、地理要 素、地理现象、地理事件,地理过程,需要采用不同的数据形式和数据类型进行描述。对于 一个地理区域,则需要从各种角度,采用不同的数据形式和数据类型,对其各个方面的性质 分别进行描述。尽管地理数据的种类是多样的,数据的信息是海量的,但是一般而言,所有 的地理数据就都具有如下的几个方面的基本特征: 2.2.1 数量化、形式化与逻辑化 (一)形式化、逻辑化与数量化,是所有地理数据的共同特征。 (二)定量化的地理数据是建立地理数学模型的基础,它有两方面的作用: (1)确定模型的参数、给定模型运行的初值条件;(2)检验模型的有效性。 (三)地理计算学,对于地理数据的形式化、逻辑化提出了更高的要求,要求“整体”和 “大容量”的地理数据具有统一的数据形式和交换标准。 地理计算学,对于地理数据的形式化、逻辑化提出了更高的要求,要求“整体”和“大 容量”的地理数据具有同一的数据形式和交换标准,从而使统一数据能够在不同的计算过程 中被使用;要求各种地理数据之间具有合理的逻辑关系,从而保证模型系统的运行剁成及计 算结果的正确性

2.2.2不确定性 不确定性是地理数据的基本特征之一。导致地理数据不确定性的原因没主要来自如下两 个方面: (一)地理系统本身的复杂性从本质上决定若地理数据的不确定性 (二)各种原因所导致的数据误差 在地理数据采集过程中 不同的数据来源、不同的 观测手段、不同的调查方法、不同的数据采集者的认识与操作水平等,都会产生地理数据的 误差不确定性。 223多种时空尺度 由于地理学的研究对象具有多种时空尺度,所以描述地理对象的地理数据也具有多种时 空尺度的性质。 (一)从空间尺度上来看,描述地理区域的各种地理数据,具有多种空间尺度一既有 全球尺度的、洲际尺度的 国家尺度的, 也有流域 度的、地区尺度的、 市尺度的、社区 尺度的。在不同的空间尺度上,地理数据的表现形式及其所包含的信息内容是不同的,为了 揭示复杂的地理空间,就必须在不同的空间尺度上对各种地理数据进行升入的解剖和分析, (二)从时间尺度上来看,描述地理过程的各种地理数据具有多种时间尺度,如历史 年代、天、月、季度、年等。在不同的时间尺度上,地理数据的表现形式及其所包含的信息 内容是不同的,为了揭示复杂的地理过程,就必须在不同的时间尺度上对各种地理数据进行 升入的解和分析 2.2.4多维性 (一)对于一个地理对象的具体意义要从空间、属性、时间三个方面综合描述。 (二)空间方面,需要描述该地理对象所处的地理位置和空间范围,一般需要2一3个 变量: (三)屈性方面,需要描述该地理对象的具体内容,至少需要1个以上,名则需要十几 个、甚至几十个变最 (四)时间方面,需要描述该地理对象产生、发展和存在的时间范围,需要1个变量: (五)地理数据的这种多维性,被人们描述为地理数据立方体(The Geographical Data Cube) 区 1,2.3,n m 图22.1地理数据立方休
2.2.2 不确定性 不确定性是地理数据的基本特征之一。导致地理数据不确定性的原因没主要来自如下两 个方面: (一)地理系统本身的复杂性从本质上决定着地理数据的不确定性。 (二)各种原因所导致的数据误差。在地理数据采集过程中,不同的数据来源、不同的 观测手段、不同的调查方法、不同的数据采集者的认识与操作水平等,都会产生地理数据的 误差不确定性。 2.2.3 多种时空尺度 由于地理学的研究对象具有多种时空尺度,所以描述地理对象的地理数据也具有多种时 空尺度的性质。 (一)从空间尺度上来看,描述地理区域的各种地理数据,具有多种空间尺度—既有 全球尺度的、洲际尺度的、国家尺度的,也有流域尺度的、地区尺度的、城市尺度的、社区 尺度的。在不同的空间尺度上,地理数据的表现形式及其所包含的信息内容是不同的,为了 揭示复杂的地理空间,就必须在不同的空间尺度上对各种地理数据进行升入的解剖和分析。 (二)从时间尺度上来看,描述地理过程的各种地理数据具有多种时间尺度,如历史 年代、天、月、季度、年等。在不同的时间尺度上,地理数据的表现形式及其所包含的信息 内容是不同的,为了揭示复杂的地理过程,就必须在不同的时间尺度上对各种地理数据进行 升入的解剖和分析。 2.2.4 多维性 (一)对于一个地理对象的具体意义要从空间、属性、时间三个方面综合描述。 (二)空间方面,需要描述该地理对象所处的地理位置和空间范围,一般需要 2~3 个 变量 ; (三)属性方面,需要描述该地理对象的具体内容,至少需要 1 个以上,多则需要十几 个、甚至几十个变量 ; (四)时间方面,需要描述该地理对象产生、发展和存在的时间范围 ,需要 1 个变量 ; (五)地理数据的这种多维性,被人们描述为地理数据立方体(The Geographical Data Cube)。 1, 2 , . m 区 域 要素 1,2,3,.,n t1 t2 . tk 时间 图 2.2.1 地理数据立方体

第3节地理数据的采集与处理 2.3.1地理数据的采集 地理数据的采集,就是运用各种技术手段,通过各种渠道搜集地理数据的过程。地理数 据采集的渠道来源主要包括如下几个方面: (一)来自于观测、测量部门的有关专业数据。警如,来自水文观测站的有关水文数据 (二) 来自于统计年鉴、统计公报中的有关自然资源及社会经济发展数据: (三)来自于有关单位或个人的不定期的典型调查数据、抽样调查数据: (四)来自于政府公报、政府文件中的有关数据: (五)来自于档案、图书等文献济料中的有关数据 (六)来自于互联网(Internet)的有关共字数据, (七)地图图件。主要包括各种比例尺的地形图 影像地图 专题地图等: (八)遥感数据。主要包括各种航空遥感数据和卫星遥感数据: (九)其它来源的有关数据。 采集地理数据的过程中需要注意以下几个问题】 一)影据的条性和可可靠性】 (二)在数据采集过程中,要采取一切可能的手段和技术措施,最大限度地减小数据的 误差 (三)在数据采集完毕后,要对各种数据质量进行检验,对不同来源的相同数据进行比 较、辨别真伪,通过数据筛选,去粗存精、去伪存真。对于残缺的但确实必须的数据,想办 法进行及时补充。 2.3,2地理数据处理 从广义上讲,任何地理问题的研究都必设计数据处理,整个研究过程就是从数据采集 到数据处理的 程 在地理学 人们千方百计地寻求和 用各种新的方法、技术和工 具,其目的就是为了准确及时地采集地理数据和有效地处理地理数据。地理数据处理,是所 有地理问题研究的核心环节。 从理论上讲,在地理雪中,数学方法的运用主要有两个目的:(1)运用数学语言对地理 问颗进行描绘,建立地理数学摸型,从根高、更深层次上揭示地理问颗的机理。(2)运用有 关数学方法,通过定量化的计算和分析,对地理数据进行处理,从而揭示有关地理现象的内 在规律。 地理数据处理是地理信息系统的核心功能。 地理计算学(Geocomputation)的实质是借助于现代化的计算理论、计算方法和计算 机技术,通过对“整体”和“大容量”的地理数据进行处理,揭示复杂地理系统的运行机制, 探索和寻求新的地理系统理论。 地 数据 理 据的 理数 GIS 数学方法 地理 Gaocompution 源 图2.3.1 地理数据采集与处理
第 3 节 地理数据的采集与处理 2.3.1 地理数据的采集 地理数据的采集,就是运用各种技术手段,通过各种渠道搜集地理数据的过程。地理数 据采集的渠道来源主要包括如下几个方面: (一)来自于观测、测量部门的有关专业数据。譬如,来自水文观测站的有关水文数据; (二) 来自于统计年鉴、统计公报中的有关自然资源及社会经济发展数据; (三)来自于有关单位或个人的不定期的典型调查数据、抽样调查数据; (四) 来自于政府公报、政府文件中的有关数据; (五)来自于档案、图书等文献资料中的有关数据; (六)来自于互联网(Internet)的有关共享数据; (七)地图图件。主要包括各种比例尺的地形图、影像地图、专题地图等; (八)遥感数据。主要包括各种航空遥感数据和卫星遥感数据; (九)其它来源的有关数据。 采集地理数据的过程中需要注意以下几个问题: (一)数据的完备性和可靠性; (二)在数据采集过程中,要采取一切可能的手段和技术措施,最大限度地减小数据的 误差; (三)在数据采集完毕后,要对各种数据质量进行检验,对不同来源的相同数据进行比 较、辨别真伪,通过数据筛选,去粗存精、去伪存真。对于残缺的但确实必须的数据,想办 法进行及时补充。 2.3.2 地理数据处理 从广义上讲,任何地理问题的研究都必设计数据处理,整个研究过程就是从数据采集 到数据处理的过程。在地理学研究中,人们千方百计地寻求和采用各种新的方法、技术和工 具,其目的就是为了准确及时地采集地理数据和有效地处理地理数据。地理数据处理,是所 有地理问题研究的核心环节。 从理论上讲,在地理雪中,数学方法的运用主要有两个目的:(1)运用数学语言对地理 问题进行描绘,建立地理数学模型,丛根高、更深层次上揭示地理问题的机理。(2)运用有 关数学方法,通过定量化的计算和分析,对地理数据进行处理,从而揭示有关地理现象的内 在规律。 地理数据处理是地理信息系统的核心功能。 地理计算学(Geocomputation)的实质是借助于现代化的计算理论、计算方法和计算 机技术,通过对“整体”和“大容量”的地理数据进行处理,揭示复杂地理系统的运行机制, 探索和寻求新的地理系统理论。 地 理 数 据 的 数 据 源 地 理 数 据 采 集 数学方法 GIS Geocomputation 地理 处理 图 2.3.1 地理数据采集与处理 数据

第4节地理数据的统计描述与处理 在地理数据的分布性质中,最重要的两个性质是集中性和腐(分)散性。数据的集中性和 离散性可用平均指标和离散指标来表示。 2.4.1地理数据的平均指标 平均指标指同类社会经济现象在一定时间、地点条件下所达到的一般水平。平均指标是 数据描述中最基本的指标之一,具有具有代表性和抽象性的特点。 (一)平均指标的作用 (1)反映总体各变量分布的集中趋势和一般水平: (2)便于比较同类现象在不同单位间的发展水平 (3)能够比较同类现象在不同时间的发展变化趋势或规律: (4)分析现象之间的依存关系: (二)平均指标的分类 平均数根据其且体的代表意义和计算方式不同.可分为数值平均数和位置平均数 (1)数值平均数 数值平均数是对总体各单位某一标志值的平均 表明总体单位标志 值的一般水平。数值平均数包括算术平均数、调和平均数、几何平均数和幂平均数 ①算术平均数算数平均数按应用条件可分为简单算数平均数和加权算术平均数。 (a)简单算数平均数计算公式如下: (2.4.1) 式中,代表平均值,x(=1,2,m)代表未做统计分组的地理数据,n为样本数据。 应用条件未分组的地理数据,各组出现的次数都是1。 例15名学生的学习成绩分别为:75、91、64、53、82。则平均成绩为: 平均成绩=75+90+64+53+82%=365-73 5 (6)加权算术平均数计算公式如下: ∫ x=可 (2.4.2) 式中,x,=1,2,m)代表第1组的中值,如果第i组下限值为a,上限值为,上限值 为b,则x=a,=(亿-a,)/2:f代表第i组的频数,即出现在第i组的地理数据个数:m 为分组个数。 应用条件分组的地理数据,各组次数不同。 表2,41工人加工某种零件资料
第 4 节 地理数据的统计描述与处理 在地理数据的分布性质中,最重要的两个性质是集中性和离(分)散性。数据的集中性和 离散性可用平均指标和离散指标来表示。 2.4.1 地理数据的平均指标 平均指标指同类社会经济现象在一定时间、地点条件下所达到的一般水平。平均指标是 数据描述中最基本的指标之一,具有具有代表性和抽象性的特点。 (一)平均指标的作用 (1)反映总体各变量分布的集中趋势和一般水平; (2)便于比较同类现象在不同单位间的发展水平; (3)能够比较同类现象在不同时间的发展变化趋势或规律; (4)分析现象之间的依存关系; (二)平均指标的分类 平均数根据其具体的代表意义和计算方式不同,可分为数值平均数和位置平均数 (1)数值平均数 数值平均数是对总体各单位某一标志值的平均,表明总体单位标志 值的一般水平。数值平均数包括算术平均数、调和平均数、几何平均数和幂平均数。 ①算术平均数 算数平均数按应用条件可分为简单算数平均数和加权算术平均数。 (a)简单算数平均数 计算公式如下: ∑ (2.4.1) = = i x n i x n 1 1 式中, x 代表平均值, ( 1, 2, , i x i = L n) 代表未做统计分组的地理数据,n 为样本数据。 应用条件 未分组的地理数据,各组出现的次数都是 1。 例 1 5 名学生的学习成绩分别为:75、91、64、53、82。则平均成绩为: 平均成绩 73 5 365 5 = ++++ 8253649075 == (b)加权算术平均数 计算公式如下: ∑ (2.4.2) ∑ = = = m m i ii f xf x 1 i i 1 式中, ( 1, 2, , ) i x i m = L 代表第 组的中值,如果第 组下限值为 ,上限值为,上限值 为 ,则 ; i i i a i b ( )/ i i ii x a ba == − 2 i f 代表第 组的频数,即出现在第i 组的地理数据个数;m 为分组个数。 i 应用条件 分组的地理数据,各组次数不同。 表 2.4.1 工人加工某种零件资料

按日产量分组(件)x 工人数(人)£ 日产总量过 14 2 28 15 4 60 16 8 128 17 5 85 18 1 18 合计 20 319 平均日产量=39=16(件) 20 重要补充:权数起若对平均数的大小起者权衡轻重的作用。平均数总是趋向于出现次数 最多的那个标志值。权数的大小是直接通过各组单位数占总体单位数的比重来确定,也就是 频率的大小体现出来的。频率的大小就直接表明了该组标志值在平均数中占据的地位,频率 越大,该标志值计入平均数的份额也越大,对平均数的影响就越大:反之,频率越小,该标 志值计入平均数的份额就越小,对平均数的影响就越小,这就是权数权衡轻重作用的实质。 值得注意的一点是,当各组的次数都相同时,各标志值对平均数的影响都相同时,那就无所 谓权数的“权衡轻重”了。在这种情况下,加权算术平均数就等于简单算术平均数。 即当==.=n时,即 (2.4.3) ∑f时 可以说,简单算术平均数实际上是加权算术平均数的特例。 ②调和平均数调和平均数是社会经济统计中常用的另一种平均指标,它是根据标志值 的倒数计算的,所以又称倒数平均数。与算术平均数一样,调和平均数有简单调和平均数和 加权调和平均数两种。 (a)简单调和平均数计算公式如下: H 2.4.40 方安买 应用条件资料未分组,各个变量值次数都是1 例3 ,个 步行两里,走第一里时速度为每小时候10里,走第二里时为每小时20里, 则平均速度为:
按日产量分组(件)x 工人数(人)f 日产总量 xf 14 2 28 15 4 60 16 8 128 17 5 85 18 1 18 合计 20 319 例 2 某车间 20 名工人加工某种零件资料,根据表(2.4.1)计算加权算术平均数。 按公式(2.4.2)可得: 平均日产量 16 20 319 == (件) 重要补充:权数起着对平均数的大小起着权衡轻重的作用。平均数总是趋向于出现次数 最多的那个标志值。权数的大小是直接通过各组单位数占总体单位数的比重来确定,也就是 频率的大小体现出来的。频率的大小就直接表明了该组标志值在平均数中占据的地位,频率 越大,该标志值计入平均数的份额也越大,对平均数的影响就越大;反之,频率越小,该标 志值计入平均数的份额就越小,对平均数的影响就越小,这就是权数权衡轻重作用的实质。 值得注意的一点是,当各组的次数都相同时,各标志值对平均数的影响都相同时,那就无所 谓权数的“权衡轻重”了。 在这种情况下,加权算术平均数就等于简单算术平均数。 即当 1 2 . n f = == f f 时,即 1 1 1 n n i i i i i ii n i i 1 n x f fx x x nf n f = = = === ∑ ∑∑ ∑ = (2.4.3) 可以说,简单算术平均数实际上是加权算术平均数的特例。 ②调和平均数 调和平均数是社会经济统计中常用的另一种平均指标,它是根据标志值 的倒数计算的,所以又称倒数平均数。与算术平均数一样,调和平均数有简单调和平均数和 加权调和平均数两种。 (a)简单调和平均数 计算公式如下: 123 111 1 1 1 n n xx x x i i n n H = x = + + +⋅⋅⋅+ = ∑ (2.4.4) 应用条件 资料未分组,各个变量值次数都是 1。 例 3 一个人步行两里,走第一里时速度为每小时候 10 里,走第二里时为每小时 20 里, 则平均速度为:
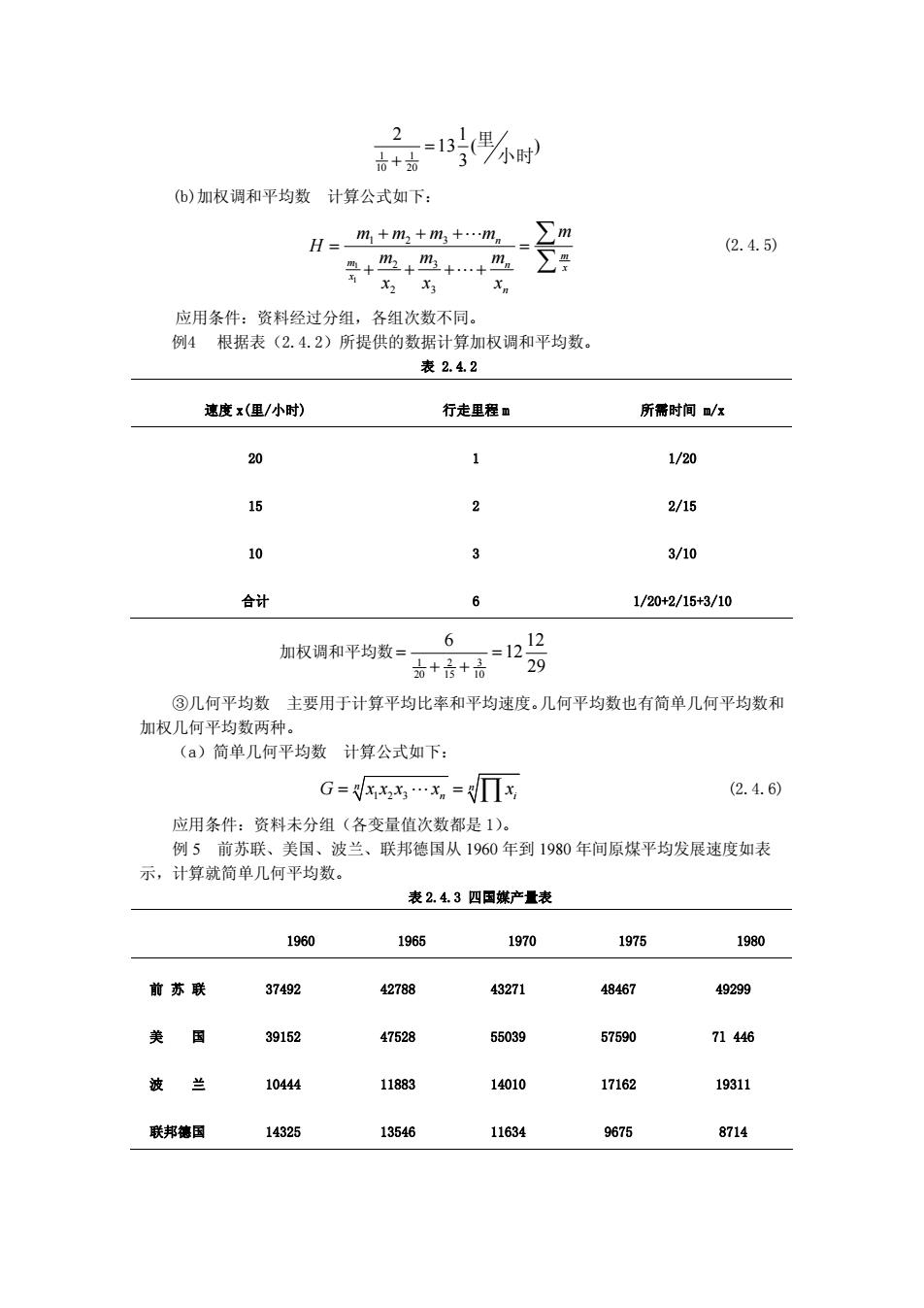
1时⅓时 2 ()加权调和平均数计算公式如下: H= m+m2+m3+.m。 (2.4.5) 应用条件:资料经过分组,各组次数不同 例4根据表(2.4.2)所提供的数据计算加权调和平均数。 表2.4.2 速度x(里/小时) 行走里程m 所需时间/x 20 1 1/20 15 2 2/15 白 3 3/10 合计 1/20+2/15+3/10 加权调和平均数= 号 6 ③几何平均数主要用于计算平均比率和平均速度。几何平均数也有简单几何平均数和 加权几何平均数两种 (a)简单几何平均数计算公式如下: G=x水.x=x (2.4.6) 应用条件:资料未分组(各变量值次数都是1)。 例5前苏联、美国、波兰、联邦德国从1960年到1980年间原煤平均发展速度如表 示,计算就简单几何平均数。 表2.43四国媒产量表 1960 1965 1970 1975 1980 前苏联37492 42788 43271 48467 49299 类国 39152 47528 5039 57590 71446 波兰 1044 11883 14010 17162 1931 联邦德国 14325 13546 11634 9675 8714
1 1 10 20 2 1 13 ( ) 3 = + 里小时 (b)加权调和平均数 计算公式如下: ∑ = ∑ +⋅⋅⋅+++ ⋅⋅⋅+++ = x m n n x m n m x m x m x m mmmm H 3 3 2 2 321 1 1 (2.4.5) 应用条件:资料经过分组,各组次数不同。 例4 根据表(2.4.2)所提供的数据计算加权调和平均数。 表 2.4.2 速度 x(里/小时) 行走里程 m 所需时间 m/x 20 1 1/20 15 2 2/15 10 3 3/10 合计 6 1/20+2/15+3/10 加权调和平均数 29 12 12 6 10 3 15 2 20 1 = ++ = ③几何平均数 主要用于计算平均比率和平均速度。几何平均数也有简单几何平均数和 加权几何平均数两种。 (a)简单几何平均数 计算公式如下: 123 n n G xxx x x = ⋅⋅⋅ = n ∏ i (2.4.6) 应用条件:资料未分组(各变量值次数都是 1)。 例 5 前苏联、美国、波兰、联邦德国从 1960 年到 1980 年间原煤平均发展速度如表 示,计算就简单几何平均数。 表 2.4.3 四国媒产量表 1960 1965 1970 1975 1980 前 苏 联 37492 42788 43271 48467 49299 美 国 39152 47528 55039 57590 7l 446 波 兰 10444 11883 14010 17162 19311 联邦德国 14325 13546 11634 9675 8714

49299 xg=37492 1.0138101.38% 19311 21044 -1.0312103.12% =0.975597.55% (b)加权几何平均数计算公式如下: (2.4.7) 应用条件资料经过分组,各组次数不同。 (2)位置平均数根据标志值某一特点位置来确定的平均数。它不是对统计数列中所有 各项数据进行计算所得的结果,而是根据数列中处于特殊位置上的个别单位或部分单位的标 志值来确定的.位晋平均新包括众数和中位数, ①众数 众数就是出现频数最多的那个数,计算方法分为以下两种情况 ()未分组的地理数据,可以根据每一个数据出现的频数大小直接确定众数。 (b)对于已经分组的地理数据,中位数的计算方法如下: 首先确定频数最多的组为众数所在组,再按以下公式计算众数: M。=L+d× △ (2.4.8) 1+△2 M。=U-d×A+A △、 (2.4.9) 上两式中,M。代表众数:L为众数所在组的下限值:U为众数所在组的上限值:△,为众数 组频数与下一组频数之差:△,为众数组频数与上一组频数之差:为众数所在组的组距。 ②中位数将各个数据从小到大排列,居于中间位置的那个数。 (a)对于未分组的地理数据,样本数n为奇数时,中位数是位置排在第(n+1)/2位的数 据:样本数为偶数时,中位数是排在中间位置的两个数据平均值。 (b)分组的地理数据,中位数的计算步骤为首先确定中位数所在的组位置,再按如下 公式计算中位数: =,泛-双 (2.4.10) 或 -2- (2.4.11) f
20 20 g 20 - 20 9755.0 97.55% 14325 8714 0312.1 103.12% 10444 19311 0305.1 103.05% 39152 71466 0138.1 101.38% 37492 49299 ٛٛ = = = = = − − g g x g χ χ χ (b)加权几何平均数 计算公式如下: 1 1 2 3 1 123 1 n n i i i n i f n f i f f f f n i G xxx x x = = = ∑ ∑ = ⋅⋅⋅ = f ∏ i (2.4.7) 应用条件 资料经过分组,各组次数不同。 (2)位置平均数 根据标志值某一特点位置来确定的平均数。它不是对统计数列中所有 各项数据进行计算所得的结果,而是根据数列中处于特殊位置上的个别单位或部分单位的标 志值来确定的.位置平均数包括众数和中位数。 ①众数 众数就是出现频数最多的那个数,计算方法 分为以下两种情况: (a)未分组的地理数据,可以根据每一个数据出现的频数大小直接确定众数。 (b)对于已经分组的地理数据,中位数的计算方法如下: 首先确定频数最多的组为众数所在组,再按以下公式计算众数: (2.4.8) 或 (2.4.9) 上两式中,M0 代表众数;L 为众数所在组的下限值;U 为众数所在组的上限值; 为众数 组频数与下一组频数之差; 为众数组频数与上一组频数之差;d 为众数所在组的组距。 Δ1 Δ2 ②中位数 将各个数据从小到大排列,居于中间位置的那个数 。 (a)对于未分组的地理数据,样本数 n 为奇数时,中位数是位置排在第(n+1)/2 位的数 据;样本数 n 为偶数时,中位数是排在中间位置的两个数据平均值。 (b)分组的地理数据,中位数的计算步骤为首先确定中位数所在的组位置,再按如下 公式计算中位数: 1 1 1 2 n i m i e m f S M Ld f − = − =+× ∑ (2.4.10) 或 m m n i i e f Sf dUM 1 2 1 1 + = − ×−= ∑ (2.4.11) 21 1 0 Δ M = dL ×+ Δ+Δ Δ 21 2 0 Δ+Δ M = dU ×−

上两式中,M代表中位数:L为中位数所在组的下限值。U为中位数所在组的上限值:∫。 为中位数所在组的频数:S,为中位数所在组以下的累计频数:S,为中位数所在组以上 的累计频数:d为中位数所在组的组距 例6下表(2.4.2)给出了某农场各农田地块的面积,试计算其中位数和众数。 表2.4.4某农场个农田地块的而积 地块编号12345 67 89101112平均值中位数众数 面积/hm12835035555072408529657554.2552.450 众数的计算先确定众数所在组。显然,众数所在的组应该在第二组。再按照公式 (2.4.8)计算众数=3476.19(元),或者按照公式(2.4.9)计算众数=3476.19(元)。 中位数的计算 先确定中数所在组的,因为,=1065所以中位应落在 二组。再按照(2.5.10)计算中位数Me=2588.46(元),或者按(2.4.11)计算中位数。 2.4.2地理数据的离散指标 前面说明了地理数据分布的集中性和一般水平,下面介绍地理数据分布的重要离散指 标。 (一)变异指标的含义变异指标是用来刻画总体分布的离散程度或变异状况,变异指 标越大,表明总体各单位标志值的变异程度越大。它是反映总体各标志值间差异程度的,且 能衡量总体平均数的代表性。常见的变异指标有极差、标准差、方差和变异系数。 (二)变异指标的作用 (1)用于衡量平均指标的代表性。 (2)反映社会经济活动的均衡 (3)研究总体标志值 布偏 正态的情况, ①极差极差是指所有数据中最大值与最小值之差。计算公式如下: R=max{x,)-min(x,) (2.4.12) 其优点是计算简便,缺点是易受极端值的影响。 ②离差离差是指每一个地理数据与平均值的差,计算公式如下: ③腐平方和高平方和是量一毛理数与平均值的离散程度。共计公 (9413 式如下: r=2x- (2.4.14) ④方差与标准差从平均概况衡量一组地理数据与平均值的离散程度。计算公式如下 2-123,-2 ni=l (2.4.15) 标准差为方差的平方根,计算公式如下: 2x- (2.4.16)
上两式中,Me 代表中位数;L 为中位数所在组的下限值。U 为中位数所在组的上限值; mf 为中位数所在组的频数; 为中位数所在组以下的累计频数; m 1 S − m 1 S + 为中位数所在组以上 的累计频数;d 为中位数所在组的组距 例 6 下表(2.4.2)给出了某农场各农田地块的面积,试计算其中位数和众数。 表 2.4.4 某农场个农田地块的面积 地块编号 1 2 3 4 5 6 7 8 9 10 11 12 平均值 中位数 众数 面积/hm2 12 83 50 35 55 50 72 40 85 29 65 75 54.25 52.4 50 众数的计算 先确定众数所在组。显然,众数所在的组应该在第二组。再按照公式 (2.4.8)计算众数M0 =3476.19 (元),或者按照公式(2.4.9)计算众数M0 =3476.19(元)。 中位数的计算 先确定中位数所在组的位置。因为, 7 1 1 1065 2 i i f = ∑ = 所以中位数应该落在第 二组。再按照(2.5.10)计算中位数 Me =2588.46(元),或者按(2.4.11)计算中位数。 2.4.2 地理数据的离散指标 前面说明了地理数据分布的集中性和一般水平,下面介绍地理数据分布的重要离散指 标。 (一)变异指标的含义 变异指标是用来刻画总体分布的离散程度或变异状况,变异指 标越大,表明总体各单位标志值的变异程度越大。它是反映总体各标志值间差异程度的,且 能衡量总体平均数的代表性。常见的变异指标有极差、标准差、方差和变异系数。 (二)变异指标的作用 (1)用于衡量平均指标的代表性。 (2)反映社会经济活动的均衡性。 (3)研究总体标志值分布偏离正态的情况。 ①极差 极差是指所有数据中最大值与最小值之差。计算公式如下: R i } (2.4.12) 其优点是计算简便,缺点是易受极端值的影响。 i i {min}{max i = − xx ②离差 离差是指每一个地理数据与平均值的差,计算公式如下: (2.4.13) ③离差平方和 离差平方和从总体上衡量一组地理数据与平均值的离散程度。其计算公 式如下: (2.4.14) ④方差与标准差 从平均概况衡量一组地理数据与平均值的离散程度。计算公式如下: (2.4.15) 标准差为方差的平方根,计算公式如下: (2.4.16) xd = xii − 2 1 = ) i d i 2 ∑( = − n xx ∑ = = − n i i xx n 1 ( 1 2) 2 σ ∑= = i − 2 σ ) n i xx n 1 ( 1