
Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 a s i s x j u.e d u c n 第五章地理学中的经典统计分 析方法 主成分分析 。 地统计分析方法 ·马尔可夫预测与趋势面分析
第五章 地理学中的经典统计分 析方法 • 主成分分析 • 地统计分析方法 • 马尔可夫预测与趋势面分析

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 w ww.o a s i s.x ju.e d u.c n atory of Oas §5.1主成分分析方法 在地理系统分析中,多变量问题是经常会遇到的, 变量太多,无疑会增加分析问题的难度与复杂性。 主成分分析就是寻找用较少的新变量代替原来较多 的旧变量,而且使新变量尽可能多地保留原来较多 信息的方法。 universitv
§5.1 主成分分析方法 在地理系统分析中,多变量问题是经常会遇到的, 变量太多,无疑会增加分析问题的难度与复杂性。 主成分分析就是寻找用较少的新变量代替原来较多 的旧变量,而且使新变量尽可能多地保留原来较多 信息的方法

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www o a s i s x j u.e d u c n 分borato0yof。asis Eco 主成分分析的基本原理 主成分分析的计算步骤 主成分分析方法应用实例 心教育部重
主成分分析的基本原理 主成分分析的计算步骤 主成分分析方法应用实例
Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www.o a s i s.x ju.e d u.c n 假定有n个地理样本,每个样本共有p个变量,构 成一个n×p阶的地理数据矩阵 (5.1.1) 基本原 X11 X12 X- X21 X22 X2P 理 绿洲生 X nl 态教 当p较大时,在p维空间中考察问题比较麻烦。 ■如果记原来的变量指标为X1,x2,.,Xp
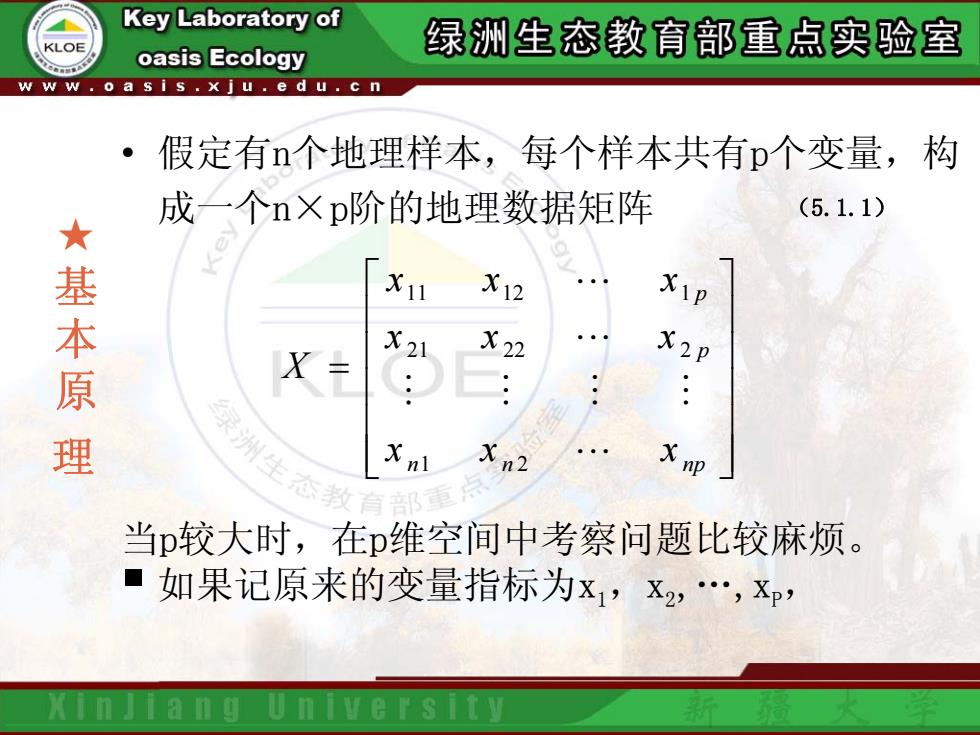
★ 基 本 原 理 • 假定有n个地理样本,每个样本共有p个变量,构 成一个n×p阶的地理数据矩阵 当p较大时,在p维空间中考察问题比较麻烦。 如果记原来的变量指标为x 1,x 2,.,x P , ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = nn np p p xx x xx x xx x X L MMMM L L 21 21 22 2 11 12 1 (5.1.1)

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 o a s i s x j u.e d u c n 它们的综合指标一新变量指标为z1,z2,.,2 (m≤p),则: 21=l1x1+12x2+.+1pxp 22=121x1+122x2+.+12pXp KL○ (5.1.2) =1m1x1+1m2x2+.+1mxp 系数1的确定原则: 部重点 ①z:与z;(i≠j: i,j-1,2,.,m)相互无关; ② Z1是X1,X2, .,xP的一切线性组合中方差最 a ng u ni ve r s l
⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ +++= +++= +++= mm m pmp pp pp xlxlxlz xlxlxlz xlxlxlz L M L L 2211 2221212 2 2121111 1 它们的综合指标—新变量指标为z 1,z 2,.,z m (m≤p),则: (5.1.2) 系数lij的确定原则: ① z i与z j ( i ≠ j;i ,j=1 , 2 , . , m)相互无关; ② z 1是x 1,x 2,.,x P的一切线性组合中方差最

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 w ww o a s i s.x j u.e d u.c n 大者,乙2是与z不相关的x1,X2,.,x的所有线性组 合中方差最大者;.; zn是与21,22,.,Zm-1都 不相关的x,x2,.,x,的所有线性组合中方差最大者。 这样决定的新变量指标z1,z2,.,z分别称为原变量 指标x1,X2’, x的第一,第二,.,第主成分。 主成分分析的主要任务就是确定每一个主成分z:在原 变量x上的载荷1
大者,z2是与z1不相关的x1,x2,.,xP的所有线性组 合中方差最大者;.;zm是与z1,z2,.,zm-1都 不相关的x1,x2,.,xP的所有线性组合中方差最大者。 这样决定的新变量指标z1,z2,.,zm分别称为原变量 指标x1,x2,.,xP的第一,第二,.,第m主成分。 主成分分析的主要任务就是确定每一个主成分zi在原 变量xj上的载荷lij

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www.o a s i s x j u.e d u c n 计算相关系数矩阵: R- 21 22 算 步 骤 式中r(i,j=l,2, p)为原变量x与x的 相关系数 ◆计算特征值与特征向量: ①解特征方程1-=0,求出特征值,并使 其按大小顺序排列,即≥≥之≥0
★ 计 算 步 骤 ◆ 计算相关系数矩阵: 式中 rij ( i ,j=1 , 2 , . , p)为原变量 xi与xj 的 相关系数 。 ◆ 计算特征值与特征向量: ① 解特征方程 ,求出特征值,并使 其按大小顺序排列,即 。 λ RI =− 0 0, λ λ21 L λp ≥≥≥≥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = pp pp p p rrr rrr rrr R L MMMM L L 21 2221 2 1211 1

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 w ww.o a s i s.x ju.ed u.cn ② 分别求出对应于特征值,的特征向量e,位=1,2,.,p) 要求le,=l,即∑e=I, 其中e表示向量的 i- 第j个分量。 ◆计算主成分贡献率及累计贡献率: ①贡献率: 之有(0=1,2,.,2) U n iversi ty
② 分别求出对应于特征值 的特征向量 要求 =1,即 ,其中 表示向量的 第j个分量。 ◆计算主成分贡献率及累计贡献率: ①贡献率: λ i pie ),2,1(i = L i e 1 1 2 ∑ = = p j ij e ij e ),2,1( 1 1 i p p k k i k k = L ∑ ∑ = = λ λ

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www o a s i s x j u e d u c n ②累计贡献率: (i=1,2,.,P) ology ◆计算主成分载荷 g-p2,xy)=V,e6,j=1,2p) (5.1.5) ◆各主成分的得分: 211 212 2m Z= 21 222 2m (5.1.6) : 22 2n吸
),2,1( 1 i p p k k i = L ∑= λ λ pjiexzpl ),2,1,(),( == λ ijijiij = L (5.1.5) ◆计算主成分载荷 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = nn nm m m zzz zzz zzz Z L MMMM L L 21 2221 2 1211 1 ◆ 各主成分的得分: (5.1.6) ②累计贡献率:

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 w ww.o a s i s.x ju.ed u.c n ★主成分分析方法应用实例 下面我们根据表3.1.1给出的数据(见第3 章),对耕地规模变化的驱动做主成分分 析,其步骤如下: (1)将表3.1.1中的数据做标准化处理,然 后就爱那个它们代入公式(5.1.4),计算 相关系数矩阵(见表5.1.1) universitv
★主成分分析方法应用实例 下面我们根据表3.1.1 给出的数据(见第3 章),对耕地规模变化的驱动做主成分分 析,其步骤如下: (1)将表3.1.1中的数据做标准化处理,然 后就爱那个它们代入公式(5.1.4),计算 相关系数矩阵(见表5.1.1)