
Multi Regression Analysis 多元回▣归分析
Multi Regression Analysis 多元回归分析

很多时候,我们研究的问题是受多个因素影响的, 需要建立多元回归方程,进行多元回归分析: 确定各个自变量对依变量的单独效应和综合效应 >对单独效应和综合效应的显著性进行测验,在自变 量中选择对依变量有显著效应的自变量,建立最优多 元回归方程 >评定各个自变量对依变量的相对重要性,以便抓住 关键因素,分析它们对所研究问题的影响程度
很多时候,我们研究的问题是受多个因素影响的, 需要建立多元回归方程,进行多元回归分析: ¾确定各个自变量对依变量的单独效应和综合效应 ¾对单独效应和综合效应的显著性进行测验,在自变 量中选择对依变量有显著效应的自变量,建立最优多 元回归方程 ¾评定各个自变量对依变量的相对重要性,以便抓住 关键因素,分析它们对所研究问题的影响程度

直线相关与回归分析回顾 在医学中,往往要研究两个定量 变量间的相互关系。如人体的血压和 脉搏,身高和体重等。统计学中的相 关与回归是研究两个变量线性关系的 最基本的方法
在医学中,往往要研究两个定量 变量间的相互关系。如人体的血压和 脉搏,身高和体重等。统计学中的相 关与回归是研究两个变量线性关系的 最基本的方法。 z直线相关与回归分析回顾
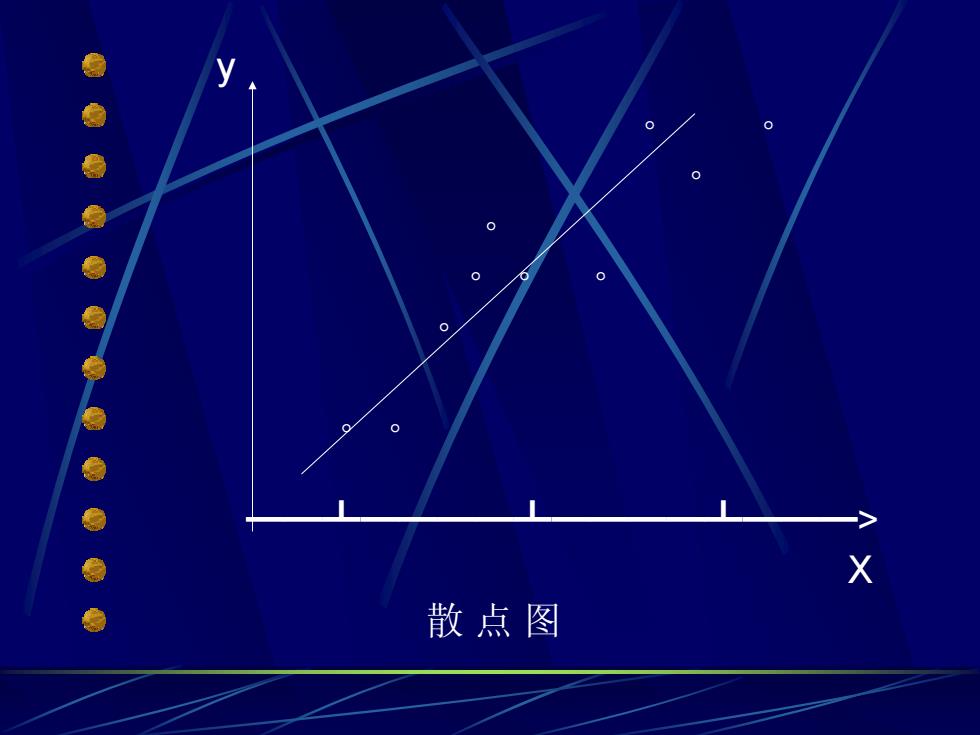
X ● 散点图
y 。 。 。 。 。 。 。 。 。 ━━┻━━━━┻━━━━┻━━━> X 散点图

线性相关 线性相关是用相关系数来表示 两个变量X,Y间的直线关系。 相关系数的计算公式 ∑X-XOY-Y X-2∑Y-)
线性相关 线性相关是用相关系数r来表示 两个变量X,Y间的直线关系。 相关系数r的计算公式 2 2)()( ))(( YYXX YYXX r −∑−∑ −−∑ =

相关系数没有单位, 在-1一+1范围内波动, 其绝对值愈接近1,两个变量间的 直线相关愈密切,愈接近0,线性相 关愈不密切
相关系数r没有单位, 在-1~+1范围内波动, 其绝对值愈接近1,两个变量间的 直线相关愈密切,愈接近0,线性相 关愈不密切

相关分析的步骤 (1)作散点图 (2)计算相关系数 (3)相关系数检验
相关分析的步骤 ( 1)作散点图 ( 2) 计算相关系数 r (3) 相关系数检验

CHISS的实现 ●点击统计→统计推断→相关矩阵
CHISS的实现 点击 统计→统计推断→相关矩阵

例9-1测得某地10名3岁儿童的体重(kg) 与体表面y(×103cm2)积,试对该资料进 行直线相关分析
例9-1 测得某地10 名 3岁儿童的体重(kg ) 与体表面 y ( ×10 3cm 2 )积,试对该资料进 行直线相关分析

直线回归 当两变量间存在着性线关系时,不 仅可以用相关系数表示变量Y与X线性 相关的密切程度,还可以用一个二元 一次方程来表示。 三 bx
当两变量间存在着性线关系时,不 仅可以用相关系数 r表示变量 Y与 X线性 相关的密切程度,还可以用一个二元 一次方程来表示。 ˆ = + bxay 直线回归