
第章因子分析 §7.1因子分析的意义和作用 一、因子分析的概念和意义 因子分析是将多个实测变量转换为少数几个不相关的综合指标的多元统计方法,在教有 领域和若其它领域的科学研究中,往往需要对反映事物、现象从多个角度进行观测,也就设 计出多个观测变量,从多个变最收集大量数据以便进行分析寻找规律。多变量大样本虽然会 为我们的科学研究提供丰富的信息,但确幽加了据采集和处理的难府。更重要的是在大名 数情况下,许多变量之间存在 一定的相关关系,从而增加了问题分析的复杂性。 因子分析就是将大最的彼此可能存在相关关系的变最转换成较少的,彼此不相关的综合 指标的一种多元统计方法。这样既可减轻收集信息的工作量,且各综合指标代表的信息不重 叠。便于分析。 二、因子分析的基本过程 子分析的基本过程可分为两个步 第 步主因子分析 是通过原始变最的相关系数矩阵内部结构的研究,导出能控制所有变量的少数几个综合 变量,通过这少数几个综合变量去描述原始的多个变量之间的相关关系。一般来说,这少数 的几个综合变量是不可观测的,故称其为因子,我们又称这种通过原始变量相关系数矩阵出 发的因子分析为R型因子分析。因子分析所获得的反映变量间本质联系、变量与公共因子的 关系的全 部信息通过导 的因子负荷矩阵体现, 第二步对因子解释和命名 从因子分析导出的负荷矩阵的结构出发,把变量按与公共因子相关性大小的程度分组, 使同组内变量间的相关性较高,不同组的变量的相关性较低,按公因子包含变量的特点(即 公因子内涵)对因子作解释命名。 三、因子分析教材在分析测验中的作用 §7,2因子分析的原理和数学模型 一、数学模型(正交因子模型) 设m个可能存在相关关系的测试变量z,2,.,乙含有P个独立的公共因子 F,F2,F,(m≥p),测试变量z,含有独特因子孔,(i1m),诸,间互不相关,且与f,(j1.p) 也互不相关,每个z:可由P个公共因子和自身对应的独特因子线性表出: Z=a,E+a2E+.+aF。+cU1 Z2=aF+azF++aF+cU2 Z=amF+amF++ampFp+cUm (7.2-1) 用矩阵表示: (cU. =(di)x z. C.U
第 章 因子分析 §7.1 因子分析的意义和作用 一、因子分析的概念和意义 因子分析是将多个实测变量转换为少数几个不相关的综合指标的多元统计方法,在教育 领域和若其它领域的科学研究中,往往需要对反映事物、现象从多个角度进行观测,也就设 计出多个观测变量,从多个变量收集大量数据以便进行分析寻找规律。多变量大样本虽然会 为我们的科学研究提供丰富的信息,但确增加了数据采集和处理的难度。更重要的是在大多 数情况下,许多变量之间存在一定的相关关系,从而增加了问题分析的复杂性。 因子分析就是将大量的彼此可能存在相关关系的变量转换成较少的,彼此不相关的综合 指标的一种多元统计方法。这样既可减轻收集信息的工作量,且各综合指标代表的信息不重 叠。便于分析。 二、因子分析的基本过程 因子分析的基本过程可分为两个步骤: 第一步 主因子分析 是通过原始变量的相关系数矩阵内部结构的研究,导出能控制所有变量的少数几个综合 变量,通过这少数几个综合变量去描述原始的多个变量之间的相关关系。一般来说,这少数 的几个综合变量是不可观测的,故称其为因子,我们又称这种通过原始变量相关系数矩阵出 发的因子分析为 R 型因子分析。因子分析所获得的反映变量间本质联系、变量与公共因子的 关系的全部信息通过导出的因子负荷矩阵体现。 第二步 对因子解释和命名 从因子分析导出的负荷矩阵的结构出发,把变量按与公共因子相关性大小的程度分组, 使同组内变量间的相关性较高,不同组的变量的相关性较低,按公因子包含变量的特点(即 公因子内涵)对因子作解释命名。 三、因子分析教材在分析测验中的作用 §7.2 因子分析的原理和数学模型 一、数学模型(正交因子模型) 设m个可能存在相关关系的测试变量z1,z2, . . ,zm 含有P个独立的公共因子 F1,F2,.,Fp(m≥p),测试变量zi含有独特因子Ui(i=1.m),诸Ui间互不相关,且与Fj(j=1.p) 也互不相关,每个zi可由P个公共因子和自身对应的独特因子Ui线性表出: ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ++++= ++++= ++++= mm m mmpmp pp pp UcFaFaFaZ UcFaFaFaZ UcFaFaFaZ L LLLLLLLLLLLLLLL L L 2211 2221122 2 22 2121111 1 11 (7.2-1) 用矩阵表示: ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ × p mm pmij m Uc Uc Uc F F F a Z Z Z M M M 22 11 2 1 2 1 .)(
为 名46品巴 (7.12y 且满足:()P≤m (II)C0W(E.)=0(即F与U是不相关的) (III)E(F)=0 COV(F)=()=I 即F,.F,不相关,且方差皆为1,均值皆为0 (IV)E(心)=0C0V()=L。即U,.不相关,且都是标准化的变量,假定z,.,z。 也是标准化的,但并不相互独立。 式中A称为因子负荷矩陈,其元素(即(72-1)中久方程的系数)a:表示第i个恋品(2.)在 第个公共因子印,上的负荷,简称因子负荷,如果把2看成P维因子空间的一个向量,则a表 示Z:在坐标轴F,上的投影。 因子分析的目的就是通过模型(?.2-1)或(72-)'。以F代Z,由于一般有P<m,从而 大到简化弯量维数的愿望」 ,因子分析中的几个重要结论 因子分析数学处理的最后结果通常以因子负荷矩阵的形式给出,这个矩阵的一般形式如 下表所示。 因子负荷矩阵的一般格式 试 因子负荷量 变量 公共度(仙的 因子1 因子2 . 因子D 1 . a a 8-2 月. 龙-2 平方和 时-s=∑∑ 百分比B=S/m P:-/m Pr=Si/m p-si/m 根据对模型(7.2-1)(或(7.2-1)的假定(①) 一(IV)可以证明有如下结论 结论1因子负荷a是Z:与F的相关系数,C是Z与的相关系数,即aP5,C=P和 证明提示: 将(亿.2-1)的第i个方程两边乘以,并求期望,运用假设条件即得广P25
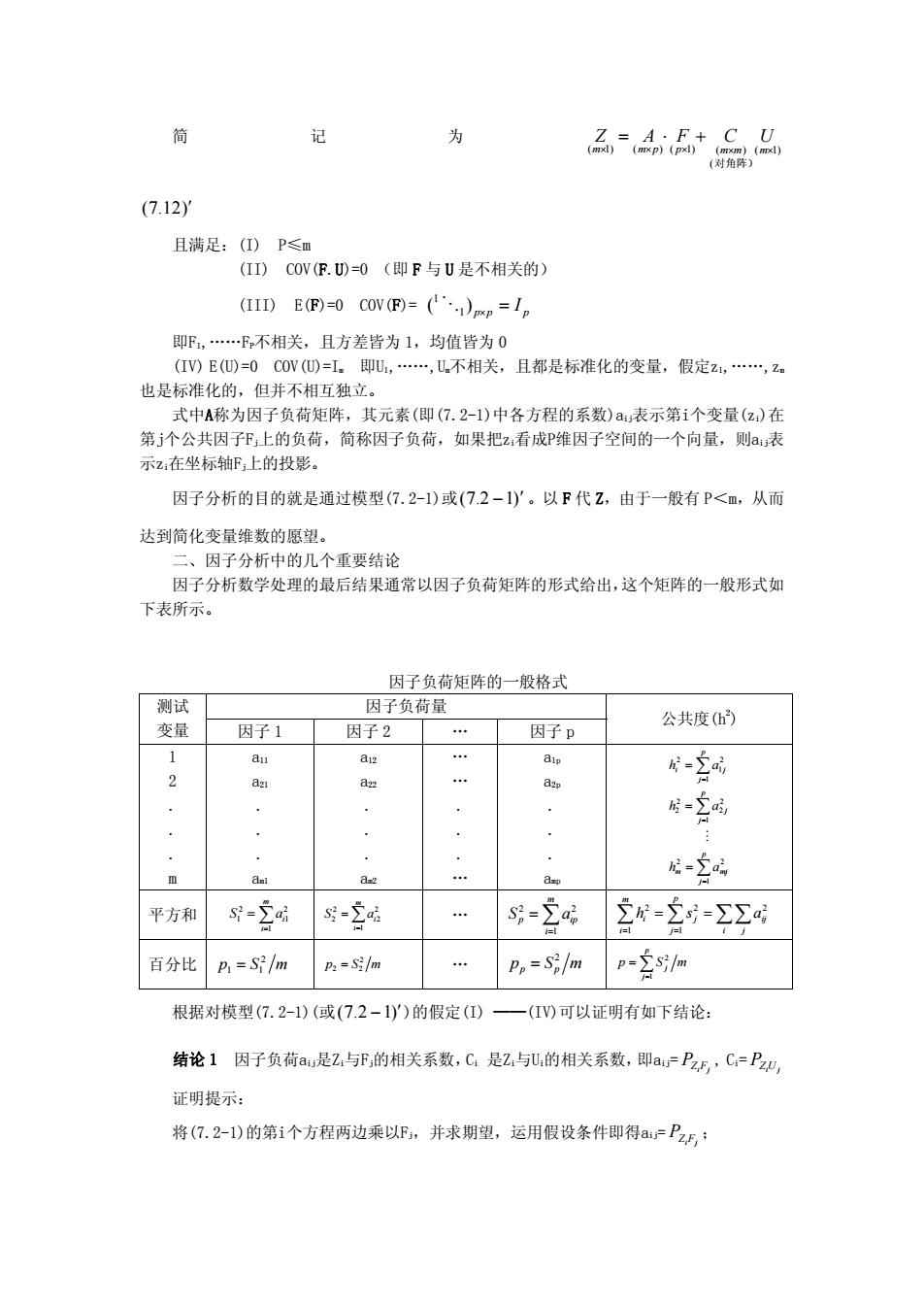
简记为 )1( ( ××× )1()()1( )( ×× = +⋅ ppmm mmm UCFAZ 对角阵) )12.7( ′ 且满足:(I) P≤m (II) COV(F.U)=0 (即 F 与 U 是不相关的) (III) E(F)=0 COV(F)= ppp = I × )( 1 1 O 即F1,.FP不相关,且方差皆为 1,均值皆为 0 (IV) E(U)=0 COV(U)=Im 即U1,.,Um不相关,且都是标准化的变量,假定z1,.,zm 也是标准化的,但并不相互独立。 式中A称为因子负荷矩阵,其元素(即(7.2-1)中各方程的系数)aij表示第i个变量(zi)在 第j个公共因子Fj上的负荷,简称因子负荷,如果把zi看成P维因子空间的一个向量,则aij表 示zi在坐标轴Fj上的投影。 因子分析的目的就是通过模型(7.2-1)或 − )12.7( ′ 。以 F 代 Z,由于一般有 P<m,从而 达到简化变量维数的愿望。 二、因子分析中的几个重要结论 因子分析数学处理的最后结果通常以因子负荷矩阵的形式给出,这个矩阵的一般形式如 下表所示。 因子负荷矩阵的一般格式 测试 因子负荷量 变量 因子 1 因子 2 . 因子 p 公共度(h2 ) 1 2 . . . m a11 a21 . . . am1 a12 a22 . . . am2 . . . . . . a1p a2p . . . amp ∑ ∑ ∑ = = = = = = p j m mj p j j p j i j ah ah ah 1 2 2 1 2 2 2 2 1 2 1 2 M 平方和 ∑= = m i i aS 1 2 1 2 1 ∑= = m i i aS 1 2 2 2 2 . ∑= = m i p aS ip 1 2 2 ∑∑ == ∑∑ = = i j ij p j j m i i ash 2 1 2 1 2 百分比 mSp 2 = 11 mSp 2 = 22 . pp mSp 2 = ∑= = p j j mSp 1 2 根据对模型(7.2-1)(或 − )12.7( ′ )的假定(I) ——(IV)可以证明有如下结论: 结论 1 因子负荷aij是Zi与Fj的相关系数,Ci 是Zi与Ui的相关系数,即aij= , C FZ ji P i= UZ ji P 证明提示: 将(7.2-1)的第i个方程两边乘以Fj,并求期望,运用假设条件即得aij= ; FZ ji P

将(亿.2-1)的第i个方程两边乘以,后求期望,由假设条件,可得C=P2 证明提示: 将(亿.2-1)中第1,j两个方程两边分别相乘后各取数学期望并利用假设条件可得结论。 结论3矩阵A中第1行平方和记为 好=立a店=1-c 证明提示: 将(7.2-1)中第1个方程两边自乘再各自求期望并运用假设条件可得。 结论4每个测试变量的方差由两部分组成: 1=D(Z,)=+c 证明提示: 对(?.2-1)第i个方程两边分别求方差并运用假设条件,我们称c为测试变量乙,的特殊 度,它表示2所含独特因子孔对忆方差所作的贡献。称为的共同度或公共度,它代表全 部公共因子对变量Z的方差所作的贡献,特别地表示第k个公共因子F对忆的方差所作的 贡献。越接近1,说明:的原始信息被所选P个公共因子解释得越好。例如:根据例1的 因子负荷阵(教材P162表7-2),h=0.932,表明2有93.2%的信息被三个公共因子说明了。 反之,当2靠近0时,说明公共因子对忆的解释很少,共信息主要由其独特因子U描述。 结论5A(a中,第列的平方和(,S-代表公共因子对所有 原始变量Z,Z,.,Z提供的方差贡献总和。 证:由前述a场的统计意义立得结论5。 由上可知:S是衡量公因子P相对重要性的指标。 百分比:S/2DZ)=S ×100%表示F,对所有测试变量的方差贡献率,其越大, m F,就越重要, 一般选择儿个公因子,就看所有公因子的方差贡献率之和(称为累计方差贡献 率)达到我们预想的百分比有儿个公因子· 以上是对正态因子模型导出的因子负荷矩阵作分析的全部依据,在实用中,我们得到的 仅是各Z的一个容量为的观测值,然后求出Z'=(亿,.,Z)的样本相关系数矩阵R用R估计
将(7.2-1)的第i个方程两边乘以Ui后求期望,由假设条件,可得Ci= UZ ii P 结论 2 ∑ (即z = = P K ZZ aaP jkik ji 1 i,zj的相关系数为矩阵A中第i,j两行向量之内积) 证明提示: 将(7.2-1)中第 i,j 两个方程两边分别相乘后各取数学期望并利用假设条件可得结论。 结论 3 矩阵 A 中 第 i 行平方和记为 2 1 2 2 1 i p k i ik ∑ −== cah = 证明提示: 将(7.2-1)中第 i 个方程两边自乘再各自求期望并运用假设条件可得。 结论 4 每个测试变量的方差由两部分组成: 22 )(1 iii +== chZD 证明提示: 对(7.2-1)第i个方程两边分别求方差并运用假设条件,我们称 为测试变量Z 2 i c i的特殊 度,它表示Zi所含独特因子Ui对Zi方差所作的贡献。称 为Z 2 hi i的共同度或公共度,它代表全 部公共因子对变量Zi的方差所作的贡献,特别地 表示第k个公共因子F 2 aik k对Zi的方差所作的 贡献。 越接近 1,说明Z 2 hi i的原始信息被所选P个公共因子解释得越好。例如:根据例 1 的 因子负荷阵(教材P162 表 7-2), 932.0 ,表明Z 2 h3 = 3有 93.2%的信息被三个公共因子说明了。 反之,当 靠近 0 时,说明公共因子对Z 2 hi i的解释很少,共信息主要由其独特因子Ui描述。 结论 5 A=(aij)中,第j列的平方和(j=1,.,p) ∑ 代表公共因子F = = m k j aS kj 1 2 2 j对所有 原始变量Z1,Z2,.,Zm提供的方差贡献总和。 证:由前述 的统计意义立得结论 5。 2 akj 由上可知: 是衡量公因子F 2 S j j相对重要性的指标。 百分比: %100)( 2 1 2 ∑ ×= = m S ZDS j m i j i 表示Fj对所有测试变量的方差贡献率,其越大, Fj就越重要,一般选择几个公因子,就看所有公因子的方差贡献率之和(称为累计方差贡献 率)达到我们预想的百分比有几个公因子。 以上是对正态因子模型导出的因子负荷矩阵作分析的全部依据,在实用中,我们得到的 仅是各Zi的一个容量为n的观测值,然后求出 Z′ =(Z1,.,Zm)的样本相关系数矩阵R用R估计

总体Z的相关系数,导出因子负荷阵,故称为R型因子分析。 §7.3公共因子的求解 要建立实际问题的因子模型,关键要根据样本数据估计因子负荷矩阵A,对A的估计方 法很多,这里仅介绍霍特林(但Hotelling)创立的,现使用较为普遍的主成份方法,(教材中 称为主因子法)。只介绍方法,不作论证。 一、因子分析从利试变量的样本相关矩陈出发 设对变量Z进行测试得容量为的观测值 21,22.,2m (i=1-m) 记, 脚%-2) 4-2- 称r为Z,Z的样本相关系数 1i.n 记R=(心)= 21123.2m 此为Z的 .0) 样本相关矩阵,是一个▣阶对称阵,再记对角阵C= 0G0.0 00.cm 其中C为模型(7.2-1)所示。 可以证明R与因子负荷阵A及C之间满足如下形式: R=A4+C2 1-c2 记R仁AA,则有RR-C 1-c2 1-c2 称R*为剩余相关矩阵,R*与R相比,仅主对角线上的元素不同,后者,主对角线全是1, 前者为1-c2=h 由于严格估计h存在困难,实际计算中有时忽略独特因子的作用,即取C:=0
总体Z的相关系数,导出因子负荷阵,故称为R型因子分析。 §7.3 公共因子的求解 要建立实际问题的因子模型,关键要根据样本数据估计因子负荷矩阵 A,对 A 的估计方 法很多,这里仅介绍霍特林(H.Hotelling)创立的,现使用较为普遍的主成份方法,(教材中 称为主因子法)。只介绍方法,不作论证。 一、因子分析从测试变量的样本相关矩阵出发。 设对变量Zi进行测试得容量为n的观测值 , )1( 21 zzz mi ii L in = — 记 jjii ij ij LL L r = 其中 ∑ ∑ ∑ = −= n k k jk k ij jkik ik zz n zzl 1 ))(( 1 ∑ ∑ = = −= n k k ii ik ik z n zl 1 2 1 2 )( 1 称rij为Zi,Zj的样本相关系数 记 此为 Z 的 mmm mm m m ij rrr rrr rrr rR × ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ == 1 1 1 )( 321 21 23 2 1312 1 L M L L 样本相关矩阵,是一个 m 阶对称阵,再记对角阵 ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = mc c c C KK KKKKK K KK 00 000 0 0 1 1 其中Ci为模型( −12.7 )所示。 可以证明 R 与因子负荷阵 A 及 C 之间满足如下形式: 2 = ′ + CAAR 记R*= AA′ ,则有 R*=R-C2 = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − 2 2 1 2 1 1 1 1 m ji ij c r c r c O 称 R*为剩余相关矩阵,R*与 R 相比,仅主对角线上的元素不同,后者,主对角线全是 1, 前者为 22 1 =− hc ii 由于严格估计 存在困难,实际计算中有时忽略独特因子的作用,即取C 2 hi i=0

(=1m),也就是令 R=AA'=(r) (7.3-3) 这里=∑00 上式就是求A的出发点,这种方法相当于预置h2=1,在此情况下提取主因子的方法称为 主分量分析,如预置的h20求相应的单位特征向量 4,巧. 为此求入,(1≤j≤p)的特征向量,即解方程组 (,-10x-i22-hmxm=0 x) (即(2,E-R):=0) -rm22.+(,-10xm=v (x 便得4,=(4,4,.4)) 再标准化便得 4、写出因子负荷阵
(i=1.m),也就是令 mmij = rAAR × = ′ )( (7.3-3) 这里 ∑= = n i ij aar jkik 1 上式就是求 A 的出发点,这种方法相当于预置 ,在此情况下提取主因子的方法称为 主分量分析,如预置的 ,则提取主因子的方法称为主因子分析。 1 2 hi = 1 2 hi < 二、求主因子解的步骤 得到测试变量 Z 的样本相关矩阵 R 之后,求主因子解还需按以下几步进行。 1、求 R 的特征根,即解方程: 0 1 1 1 || 1 2 21 2 12 1 = −− − −−− −− − =− λ λ λ λ K KKKK K K m m m m rr r r rr RE 由R是非负定阵,解出的特征值都是非负的,将其非零特征值按从大到小排序并重新编码: λ1≥λ2≥.0 2、按预先规定所取的 P 个公共因子的累计方差贡献率达到的百分比(一般取 85%) 使 85.0 1 1 ≥ ∑ ∑= m i p i i λ λ 的P即为所取的公因子数(可以证明 m sk m i k ∑ i = =1 λλ 第k个公共因子Fk的 方差贡献率)。 3、对选定的前P个特征值λ1≥λ2≥.≥λp>0 求相应的单位特征向量 oo LL o uuu p , 21 。 为此求λj(1≤j≤p)的特征向量uj,即解方程组: ⎪ ⎩ ⎪ ⎨ ⎧ =−+−− =−−−− xrxr vx xrxrx m m mj j mm )1( )1( 0 2211 2121 1 λ λ L LLLLLLLLLLLLL L ( = 0) ) ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − m i j x x 即(λ RE M 便得 ),( 21 = ′ Luuuu mjjjj 再标准化便得 o u j 4、写出因子负荷阵

GV万2v万:GpV 2V月 §74求出主因子解后的进一步分析 一、因子旋转 建立因子分析数学摸型的目的不仅要找出公共因子并对变量进行分组,史重婴的是要知 道每个公共因子的意义,以便对实际问题作出科学分析。不难理解,由(亿.3-3)出发解出的 因子负荷阵是不唯一的,事实上,用一个正交矩阵T右乘A: (ATXAT)=A(TT)A'=AA=R 即知A在正交变换T下也是因子负荷阵 为此,当A的结构不使对主因子进行解释时,我们根据因子负荷阵的不唯一性,可用 个正交阵右乘A(即对A实施一个正交变换)由线性代数的知识,对A施行一个正交变换,对 应坐标系就有一次施转。因此我们称这种变换A的方法为因子轴的旋转,我们的目的要使初 始因子负荷阵A经 一系列旋转后结构简化 即达到以下原则 1、每个公共因子只在少数几个测试变量上具有高负荷,其余负荷很小或至多中等大。 2、每个测试变量仅在一个公共因子上有较大负荷,而在其余公共因子上的负荷较小或 至名只中等大小, 可见,惊转的目的是使每一个测试矢量在新的华标轴上的射影尽可能向1和0两极分化 对因子负荷阵旋转的方法有多种,如正交旋转,斜交旋转等,这里只介绍常用的Kaiser提 出的方差极大正交旋转法(Varimax法),为说明该旋转法的原理 首先考虑P=2的情形。设因子负荷阵 A=an an 再按行计算公共度h=a1+a22i=l.,m 考虑到各个变量Z:的公度之间的差异所造成的不平衡,需对中元素作规格化处理,即 每行元素用每行的公共度除,为简便规格化后的A,仍记为A=(a,/h,)=(@) 取正交阵7-cos,-sinp 记B=(b,)=A7 sino,coso an coso+dizsino.-di sin+diz cosobb 则B= 。 a coso+a sin, -am sino+am2 cosob b2 为使B达到结构简化,就须使旋转后的因子负荷阵B的两列元素的平方值向0和1两极分化(即 两个公共因子对实测变量Z的贡献越分散越好,这实际上希望将变量乙,乙,.乙分成两组, 一组主要与第一主因子有关,另一组主要与第二主因子有关),因此要求
⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = m m pmp pp pp uu u uu u uu u A λλ λ λλ λ λλ λ o o o o o o o o o M MMMM M M 2211 122121 2 212111 1 §7.4 求出主因子解后的进一步分析 一、因子旋转 建立因子分析数学模型的目的不仅要找出公共因子并对变量进行分组,更重要的是要知 道每个公共因子的意义,以便对实际问题作出科学分析。不难理解,由(7.3-3)出发解出的 因子负荷阵是不唯一的,事实上,用一个正交矩阵 T 右乘 A: ′ = )())(( ′′ = ′ = RAAATTAATAT 即知 A 在正交变换 T 下也是因子负荷阵 为此,当 A 的结构不便对主因子进行解释时,我们根据因子负荷阵的不唯一性,可用一 个正交阵右乘 A(即对 A 实施一个正交变换)由线性代数的知识,对 A 施行一个正交变换,对 应坐标系就有一次施转。因此我们称这种变换 A 的方法为因子轴的旋转,我们的目的要使初 始因子负荷阵 A 经一系列旋转后结构简化,即达到以下原则: 1、每个公共因子只在少数几个测试变量上具有高负荷,其余负荷很小或至多中等大。 2、每个测试变量仅在一个公共因子上有较大负荷,而在其余公共因子上的负荷较小或 至多是中等大小。 可见,旋转的目的是使每一个测试矢量在新的坐标轴上的射影尽可能向 1和 0两极分化。 对因子负荷阵旋转的方法有多种,如正交旋转,斜交旋转等,这里只介绍常用的 Kaiser 提 出的方差极大正交旋转法(Varimax 法),为说明该旋转法的原理 首先考虑 P=2 的情形。设因子负荷阵 再按行计算公共度 ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 2 22 12 1 21 11 amm a a a a a A LL iii ,1 miaah 2 2 2 1 2 =+= L 考虑到各个变量Zi的公度之间的差异所造成的不平衡,需对A中元素作规格化处理,即 每行元素用每行的公共度除,为简便规格化后的A,仍记为A= )()( ijiij = aha ′ Δ 取正交阵 记 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = ϕϕ ϕϕ cos,sin sin,cos T ij == ATbB Δ )( 则 ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ′ + ′ − ′ + ′ ′ + ′ − ′ + ′ = Δ 1 2 11 12 1 2 1 2 11 12 11 12 cos ,sin sin cos cos sin,sin cos m m m m m bb m bb aa aa aa aa B M MMM ϕ ϕ ϕ ϕ ϕϕ ϕϕ 为使B达到结构简化,就须使旋转后的因子负荷阵B的两列元素的平方值向 0和 1两极分化(即 两个公共因子对实测变量Z的贡献越分散越好,这实际上希望将变量Z1,Z2,.Zm分成两组, 一组主要与第一主因子有关,另一组主要与第二主因子有关),因此要求

(6品,.b品,(6,.b品) 两组数据的(样本)方差和V,尽可能大,为此,正交旋转的角度p应满足使 +=V=max 即 r-立之r-(立1=mx (7.4-1) 由微积分求最值原理令小=0 do (:b,与p有关,故v与p有关) 可解出:g4p=。-a-bm d-2ablm 若记y,=(aa/h,)2-(a2/h)2 w,=2(aa/h,)(a2/h) =an-an =2anan 则a=立b=∑mc=2(-.d=22 根据g4p的表达式中分子、分母的符号确定口角的取值范围如下表: 分子符号 分母符号 40取值范用 p取值范围 + 0-8 2 84 π开 48 + -0 _π-0 8 一般地,如公共因子有P个,则需逐次对每两个公共因子进行上述旋转,实际上,当公共因 子P>2时,可以每次取两个,全部配对旋转,例如取F,,F两个主因子配对旋转时,正 交变换阵如教材P172.所示,这一旋转只是对规格化后的因子负荷阵A的第I列,g列两 列进行,其余的元素不变,此时,公式(7.4-1)中只须将b,换成b,b换成b,旋转角计算 式中出现a,a2之处政为a,a。即可,易理解,共需C=P+》次旋转,算是一轮
),(),( 2 2 2 12 2 1 2 11 L m Lbbbb m 两组数据的(样本)方差V1和V2尽可能大,为此,正交旋转的角度ϕ 应满足使 max 21 ==+ Δ VVV 即 max]) 1 ()( 1 [ 2 1 2 2 1 2 2 1 = − ∑∑∑ = == = m i ij m i ij j b m b m V (7.4-1) 由微积分求最值原理 令 = 0 dϕ dv (∵bij与ϕ 有关,故V与ϕ 有关) 可解出: mbac mabd tg )( 2 4 22 −− − ϕ = 若记 2 2 2 1 )()( = iii − hahav ii i = 1 2 hahaw iiii )()(2 2 2 2 1 aa ii = ′ − ′ 2 aa ii 21 = ′ ′ 则 ∑∑∑ ∑ = = = = == =−= m i i ii m i i m i i m i i wvdwvcwbva 1 2 1 2 1 1 2),(., 根据tg4ϕ 的表达式中分子、分母的符号确定ϕ 角的取值范围如下表: 分子符号 分母符号 4ϕ 取值范围 ϕ 取值范围 + + 2 ~0 π 8 ~0 π + — π π ~ 2 4 ~ 8 π π — — 2 ~ π π −− 8 ~ 4 π π −− — + 0~ 2 π − 0~ 8 π − 一般地,如公共因子有P个,则需逐次对每两个公共因子进行上述旋转,实际上,当公共因 子P>2 时,可以每次取两个,全部配对旋转,例如取 , 两个主因子配对旋转时,正 交变换阵如教材P172 所示,这一旋转只是对规格化后的因子负荷阵A的第 列,g列两 列进行,其余的元素不变,此时,公式(7.4-1)中只须将 换成b Fl Fg l g T l bil iz, bii换成big,旋转角计算 式中出现 ai1 , ai2之处改为 ail , aig 即可,易理解,共需 2 )1( 2 + = pp Cp 次旋转,算是一轮

循环完华,记=左y,=左之6》-2GP.(74-少 则V是第一轮旋转后所得因子负荷阵的总方差,如果我们对第一轮旋转后所得因子负荷阵 B=ATIg.Tp-l 不满意,还可以重新开始进行第二轮C2次配对旋转,并计算V如此继续下去,直到进行S 次重复循环后,对预先设定的很小正数£有V-V-K8便认为达到方差极大正交脑 转的目的而终止,以上复杂的变换过程,可用SPSS等统计软件在电脑上实现,最后得到的B, 即为旋转后的因子负荷矩阵,而B的因子负荷己向两极分化,更便利于对各公共因子作解释 并命名。 §7.5因子分析在Statistica中的实现 因子分析是通过研究多个指标相关矩阵的内部依赖关系,找出控制所有变量的少数公 因子,将每个指标变量表示成公因子的线性组合,以再现原始变量与因子之间的相关关系。 因子分析的目的是寻求变量基本结构,简化观测系统,减少变量维数,用少数的变量来解释 整个问恩。在分析处理多变量问墨时,变量间往往相关性极为密切,使得观测数据所反映的 信息有重叠。因此,用户希望能找出较少综合变量尽可能地反映原来变量的信息,有彼此之 间是互不相关,这些不可观测的少数几个综合变量成为公共因子。因子分析可根据用户选定 的提取共因子方法与初始因子载荷矩阵的旋转方式,输出变量的特征值,总的方差百分比, 累计特征值,累计方差百分比,旋转后的因子成分矩阵,碎石图等。 例1基于因子分析的新疆土地利用经济效益分析 新疆维吾尔自治区地处亚欧大陆中心,是典型的干早半干早地区。其土地面积辽阔但 沙漠、酥漠、戈壁、盐漠、裸岩等目前尚不能利用或难以利用的士地面积很大,约占全疆士 地总面积的48.24%。根据新疆维吾尔自治区土地利用现状调查和1992年土地详查的汇总数 据,在己利用面积中,农业用地为6067.94×10hm2,占全疆总面积的36.75%,占己利用面 积的91.5%:非农业用地为538.55×10m,占全疆总面积的3.26%,占己利用地面积的 8.15x四新疆的总土地利用率为38.57%,未利用士地面积占士地总面积的61.43%四,是全国 土地利用率最低的省区之 运用因子分析法,利用2006年统计年鉴的最新数据,对新疆15个地州(市)进行定量 分析。以期对新疆维吾尔自治区的士地利用经济效益有个及时全面地认识,并能够提出可行 的提高土地利用经济效益的措施。 上地利用是人类最基本的经济活动,其目标是取得经济效益、社会效益和生态效益。士 地利用所得到的各种成果与劳动消耗(包括劳动占用)的相关评价统称为士地利用经济效益 通过研究土地利用的经济效益,可以确定合理的土地利用方式、结构及布局,从而实现土地 资源的可持续利用。 目前,土地利用的社会效益和生态效益定量研究比较困难,较为常见的是土地经济效湖 的定量评价,但是相对而言,此类研究仍然比较少。已有的对土地利用的经济效益进行了探 索性研究的包括:南京农业大学士地管理学院减俊梅、马连营若作的新餐士地利用的经济 益初探,新疆农业大学陈玉兰、苏武铮的新疆土地利用经济效益综合分析及评价,内蒙古 范大学地理科学学院阿拉腾图雅、宝音等著的内蒙古土地利用现状及其经济效益分析,中国 科学院地理科学与资源研究所吕晓芳、张镂锂等的宁夏中部生态脆弱区土地资源利用现状及
循环完毕,记 )14.7(})]( 1 [)( 1 { 2 1 1 22 2 1 1 )1( == ∑∑ ∑ ∑ − − ′ = = = = L m i m i ij ij p j p j j b m b m VV 则V(1)是第一轮旋转后所得因子负荷阵的总方差,如果我们对第一轮旋转后所得因子负荷阵 1 = 1312 LTTATB − ,1 pp 不满意,还可以重新开始进行第二轮 次配对旋转,并计算V 2 Cp (2)如此继续下去,直到进行S 次重复循环后,对预先设定的很小正数ε 有 − < ε − | | VV ss )1()( 便认为达到方差极大正交旋 转的目的而终止,以上复杂的变换过程,可用SPSS等统计软件在电脑上实现,最后得到的Bs 即为旋转后的因子负荷矩阵,而Bs的因子负荷已向两极分化,更便利于对各公共因子作解释 并命名。 §7.5 因子分析在 Statistica 中的实现 因子分析是通过研究多个指标相关矩阵的内部依赖关系,找出控制所有变量的少数公 因子,将每个指标变量表示成公因子的线性组合,以再现原始变量与因子之间的相关关系。 因子分析的目的是寻求变量基本结构,简化观测系统,减少变量维数,用少数的变量来解释 整个问题。在分析处理多变量问题时,变量间往往相关性极为密切,使得观测数据所反映的 信息有重叠。因此,用户希望能找出较少综合变量尽可能地反映原来变量的信息,有彼此之 间是互不相关,这些不可观测的少数几个综合变量成为公共因子。因子分析可根据用户选定 的提取共因子方法与初始因子载荷矩阵的旋转方式,输出变量的特征值,总的方差百分比, 累计特征值,累计方差百分比,旋转后的因子成分矩阵,碎石图等。 例 1 基于因子分析的新疆土地利用经济效益分析 新疆维吾尔自治区地处亚欧大陆中心,是典型的干旱半干旱地区。其土地面积辽阔但 沙漠、砾漠、戈壁、盐漠、裸岩等目前尚不能利用或难以利用的土地面积很大,约占全疆土 地总面积的 48.24%。根据新疆维吾尔自治区土地利用现状调查和 1992 年土地详查的汇总数 据,在已利用面积中,农业用地为 6067.94×104 hm2 ,占全疆总面积的 36.75%,占已利用面 积的 91.5%;非农业用地为 538.55×104 hm2 ,占全疆总面积的 3.26%,占已利用地面积的 8.15%[1]新疆的总土地利用率为 38.57%,未利用土地面积占土地总面积的 61.43% [2],是全国 土地利用率最低的省区之一。 运用因子分析法,利用 2006 年统计年鉴的最新数据,对新疆 15 个地州(市)进行定量 分析。以期对新疆维吾尔自治区的土地利用经济效益有个及时全面地认识,并能够提出可行 的提高土地利用经济效益的措施。 土地利用是人类最基本的经济活动,其目标是取得经济效益、社会效益和生态效益。土 地利用所得到的各种成果与劳动消耗(包括劳动占用)的相关评价统称为土地利用经济效益。 通过研究土地利用的经济效益,可以确定合理的土地利用方式、结构及布局,从而实现土地 资源的可持续利用。 目前,土地利用的社会效益和生态效益定量研究比较困难,较为常见的是土地经济效益 的定量评价,但是相对而言,此类研究仍然比较少。已有的对土地利用的经济效益进行了探 索性研究的包括:南京农业大学土地管理学院臧俊梅、马连营著作的新疆土地利用的经济效 益初探,新疆农业大学陈玉兰、苏武铮的新疆土地利用经济效益综合分析及评价,内蒙古师 范大学地理科学学院阿拉腾图雅、宝音等著的内蒙古土地利用现状及其经济效益分析,中国 科学院地理科学与资源研究所吕晓芳、张镒锂等的宁夏中部生态脆弱区土地资源利用现状及

经济效益分析,东北农业大学资源与环境学院李画岩、王红梅的基于SPSS的黑龙江省土地利 用经济效益分析 新疆维吾尔自治区作为干早半干早地区的典型代表之一,其不仅具有干早半干早地区所 共有的特点,还有其自身的许多特点。由于新疆地域辽 ,即使是同在 省 不同的地区特 点也不尽相同,尤其在土地利用方面:首先,新疆土地利用率较低。这不仅取决于新疆有限 的水资源,而且受新疆生产力水平的限制:其次,新疆土地利用布局分散,这是由新疆土地 资源的利用直接依赖于水资源而决定的,这种土地利用格局既限制了土地利用的规模效益, 也影响了土地利用的结构与布局:第三,我区土地利用类型的多样化,新疆丰富的自然资源 为国民经济的全面发展创造了条 土地利用的类型也呈现出多样化特点。据自 区的士地 详查,除八大类 -级地类外,全疆士地的二级地类达44个,占全国47个 二级地类数的93.6 第四,土地开发利用的难度较大由于水资源在地区之间、季节之间分布不均衡,开发利用士 地必须进行大规模的水利工程建设,并建立完善配套的灌排渠系,土地开发的成本较高:第 五,土恤生态环培脆弱,据1990年以来的统计资料分折,新疆年均受灾率16.5%,虽低于 全国33.6%的水平, 但成灾率达65.6%,高出全国50.3%水平达15.3个百分点。因此 东、 南疆的不少地区(优其是沙漠前沿地区) 生态环境的治理与建设,是确保土地持续利 用、经济持续发展的重要关键。 指标体系构建原则 遵循科学性、系统性、可操作性等原则选取指标 科学性原则:即所确定的指标体系必须立足客观现实,建立在准确、科学的基础上,应 建立在充分认识经济效益与 上地利用的特点、 系统研究 地利用的目标、原则与影响因素等 基础上,并能客观反映合理用地内涵,较好地量度土地利用的合理性、适宜性和可持续性。 所选指标的集合能够反映区域资源、环境、人口、经济和社会等方面发展的真实水平。 整体性原则:土地利用是一个复杂的自然、经济、社会、生态相统一的系统工程,经汉 效益是以尽量少的劳动耗费取得尽量多的经营成果,它是衡量一切经济活动最终的综合指 所选的指标体系必 能 面 反映 域发展的综合水平以及各方面发展的因素指材 指标体系的各个指标之间不是简单相加,而是有机联系而组成一个层次分明的系统整体,但 同级指标之间应保持各自的独立性,避免指标之间的复交义、相互包含及大同小异现象 可操作性原则:要避免指标过名和相互之间不必要的重叠。所洗择的指标要具有代表性 和可操作性,指标内容应简单明了,容易理解,可比性强,并尽可能量化。指标值通常可以 人 百分比、增长率或效益等表示 相关性原则:指标的 择还要与所研究的问题和目的相关。所选的指标应该直接或间接 与土地利用和经济效益有关,没有关系的指标就应该努力建立起关系,否则就摈弃四。 总之,指标体系的构建应选取覆盖面宽、有代表性、能够反映研究区经济社会状况对士 地利用经济效益变化产生影响的因素。 通过分析研究,并结合前人的究成果卧同,本文体结合了新疆维吾尔自治区15个 地(州)市的实阿 情况 选择了10个指标来构成了土地利用经济效益的指标体系,他们分 别是:X-人均耕地(m,人):X-人均建设用地(m·人):X-人均国内生产总值(元·人 ):X-域镇化水平(%):X-农用地均产值(元·m):X。-建设用地均产值(元·hm): X-第一产业占三产比重(%):X-第二三产业占三产比重(%):X-农用地结构(%):X。 建设用地结构(%)。以这一指标体系为基础,结合相应的数据作新疆土地经济效益的定量分 析研究 软件操作 1.建立数据文件: 因子分析过程
经济效益分析,东北农业大学资源与环境学院李丽岩、王红梅的基于SPSS的黑龙江省土地利 用经济效益分析[3-8] 。 新疆维吾尔自治区作为干旱半干旱地区的典型代表之一,其不仅具有干旱半干旱地区所 共有的特点,还有其自身的许多特点。由于新疆地域辽阔,即使是同在一省,不同的地区特 点也不尽相同,尤其在土地利用方面:首先,新疆土地利用率较低。这不仅取决于新疆有限 的水资源,而且受新疆生产力水平的限制;其次,新疆土地利用布局分散,这是由新疆土地 资源的利用直接依赖于水资源而决定的,这种土地利用格局既限制了土地利用的规模效益, 也影响了土地利用的结构与布局;第三,我区土地利用类型的多样化,新疆丰富的自然资源 为国民经济的全面发展创造了条件,土地利用的类型也呈现出多样化特点。据自治区的土地 详查,除八大类一级地类外,全疆土地的二级地类达 44 个,占全国 47 个二级地类数的 93.6%; 第四,土地开发利用的难度较大由于水资源在地区之间、季节之间分布不均衡,开发利用土 地必须进行大规模的水利工程建设,并建立完善配套的灌排渠系,土地开发的成本较高;第 五,土地生态环境脆弱,据 1990 年以来的统计资料分析,新疆年均受灾率 16.5%,虽低于 全国 33.6%的水平,但成灾率达 65.6%,高出全国 50.3%水平达 15.3 个百分点[2]。因此,在 东疆、南疆的不少地区(尤其是沙漠前沿地区),生态环境的治理与建设,是确保土地持续利 用、经济持续发展的重要关键。 指标体系构建原则 遵循科学性、系统性、可操作性等原则选取指标: 科学性原则:即所确定的指标体系必须立足客观现实,建立在准确、科学的基础上,应 建立在充分认识经济效益与土地利用的特点、系统研究土地利用的目标、原则与影响因素等 基础上,并能客观反映合理用地内涵,较好地量度土地利用的合理性、适宜性和可持续性。 所选指标的集合能够反映区域资源、环境、人口、经济和社会等方面发展的真实水平。 整体性原则:土地利用是一个复杂的自然、经济、社会、生态相统一的系统工程,经济 效益是以尽量少的劳动耗费取得尽量多的经营成果,它是衡量一切经济活动最终的综合指 标。所选的指标体系必须能够全面地反映区域发展的综合水平以及各方面发展的因素指标, 指标体系的各个指标之间不是简单相加,而是有机联系而组成一个层次分明的系统整体,但 同级指标之间应保持各自的独立性,避免指标之间的复交叉、相互包含及大同小异现象。 可操作性原则:要避免指标过多和相互之间不必要的重叠。所选择的指标要具有代表性 和可操作性,指标内容应简单明了,容易理解,可比性强,并尽可能量化。指标值通常可以 人均、百分比、增长率或效益等表示。 相关性原则:指标的选择还要与所研究的问题和目的相关。所选的指标应该直接或间接 与土地利用和经济效益有关,没有关系的指标就应该努力建立起关系,否则就摈弃[22] 。 总之,指标体系的构建应选取覆盖面宽、有代表性、能够反映研究区经济社会状况对土 地利用经济效益变化产生影响的因素。 通过分析研究,并结合前人的研究成果[3]-[6],本文具体结合了新疆维吾尔自治区 15 个 地(州)市的实际情况,选择了 10 个指标来构成了土地利用经济效益的指标体系,他们分 别是:X1 -人均耕地(hm2 ·人-1);X2 -人均建设用地(hm2 ·人-1);X3 -人均国内生产总值(元·人 -1);X4 -城镇化水平(%);X5 -农用地均产值(元·hm-2);X6 -建设用地均产值(元·hm-2); X7 -第一产业占三产比重(%);X8 -第二三产业占三产比重(%);X9 -农用地结构(%);X10 - 建设用地结构(%)。以这一指标体系为基础,结合相应的数据作新疆土地经济效益的定量分 析研究。 软件操作 1.建立数据文件: 因子分析过程

借助于STATISTICA6.0软件,使用Statistica中的ultivariate explorator 指园的i过指进行分浙。指始指木电珠标准化标准化道 致和数量级差异大等现 ,然后建立变量的相关系 数矩阵R(表】 相关系数矩阵能够反映各变量之间的关系。并计算出R的特征值和贡献率(表2)。贡献率 反映每个因子所包含原始数据信息量的大小,由累计贡献率可知前3个因子已包含了原始数 据80.94%的信息,满足了因子分析>80%以上的要求。所以,取前3个因子做因子分析。 表1各变量相关系数矩阵表 Tah.1 The variable correlation coefficient matrix . X. 光名w 1.00 名0.156 1.000 X3-0.0500.5241.000 X06200.4750.556 1.000 .0947 -0204-01R3015g 1000 =02280007 0.608 1000 X 0.29 -0.235 0.546 0.41g 0.2 -0.8251.0m0 -0.2930.235 0.546 0.419 0.220 0.825 -1.0001.000 X0.264 -0.0010.0230.312 -0.490-0.0980.160-0.1601.000 X0-0.2430.4350.8940.465 -01g20680 -0.5150.5150.1761.000 表2变量特征值与贡献率表 Tab.2 Eigen able of the variables 特征值 页献率% 浆计页献率% 1 4.324026 43.24026 43.2403 2.114724 21.14724 64.3875 654864 16.5486 80.936 0.9855 9.8552 90.791 5 0.599888 5.99888 96.7902 6 0.181122 1.81122 98.6014 7 0.094880 0.94880 99.5502 0.3 9 9 0.01014 0.1014 10.000 提取后的主因子为图表中的前三个因子,可表示为因子一、因子二、因子三(E、F2、F,)。 为了更清楚地反映变量之间的关系,对得到的初始因子载荷进行正交旋转,正交旋转后,可 以使载荷矩阵能更好地反映数据间的关系。得到主因子载荷矩阵(表3)。由旋转后的载荷 矩阵可以 第 主因了,在X、X、X上有较大载荷,而这3个指标分别是人均耕地、第一产业 三产比重、农用地结构,它们主要从农用地方面反映了土地利用经济效益,定名为“农用地 因子”。新疆的农用地主要分布在绿洲,农用地的利用程度可以反映新疆绿洲农业经济的发 展状况。 第二个主因子F:在X、X、X、 X上有较大载荷,这五个指标分别是人均耕地、人均 建设用地、人均国内总产值、建设用地结构,他们反映了士地利用经济效益在建设用地利用 方面的实力,定名为“建设用地水平因子”。建设用地是影响土地利用结构、土地利用率、 土地可持续发展的重要因素之一,同时也是耕地的面积和保护的控制因素之一。 第三个主因子F在X,X,X、X,上有较大载荷,这4个指标分别是农用地均产
借助于 STATISTICA6.0 软件,使用 Statistica 中的 Multivariate Exploratory Techniques 下的 Factor Analysis 过程进行分析。将原始样本矩阵标准化,标准化可以消 除指标之间量纲的不一致和数量级差异大等现象,然后建立变量的相关系数矩阵 R(表 1), 相关系数矩阵能够反映各变量之间的关系。并计算出 R 的特征值和贡献率(表2)。贡献率 反映每个因子所包含原始数据信息量的大小,由累计贡献率可知前 3 个因子已包含了原始数 据 80.94%的信息,满足了因子分析>80%以上的要求。所以,取前 3 个因子做因子分析。 表 1 各变量相关系数矩阵表 Tab. 1 The variable correlation coefficient matrix X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X1 1.000 X2 0.156 1.000 X3 -0.050 0.524 1.000 X4 0.620 0.475 0.556 1.000 X5 0.247 -0.304 -0.133 0.159 1.000 X6 -0.228 0.007 0.606 0.456 0.344 1.000 X7 0.293 -0.235 -0.546 -0.419 -0.220 -0.825 1.000 X8 -0.293 0.235 0.546 0.419 0.220 0.825 -1.000 1.000 X9 0.264 -0.001 0.023 0.312 -0.490 -0.098 0.160 -0.160 1.000 X10 -0.243 0.435 0.894 0.465 -0.192 0.680 -0.515 0.515 0.176 1.000 表 2 变量特征值与贡献率表 Tab.2 Eigenvalue and Cumulative table of the variables 特征值 贡献率% 累计贡献率% 1 4.324026 43.24026 43.2403 2 2.114724 21.14724 64.3875 3 1.654864 16.54864 80.9361 4 0.985520 9.85520 90.7913 5 0.599888 5.99888 96.7902 6 0.181122 1.81122 98.6014 7 0.094880 0.94880 99.5502 8 0.034827 0.34827 99.8985 9 0.010148 0.10148 100.0000 提取后的主因子为图表中的前三个因子,可表示为因子一、因子二、因子三(F1、F2、F3)。 为了更清楚地反映变量之间的关系,对得到的初始因子载荷进行正交旋转,正交旋转后,可 以使载荷矩阵能更好地反映数据间的关系。得到主因子载荷矩阵(表3)。由旋转后的载荷 矩阵可以看出: 第一个主因子F1 在X1、X7、X9上有较大载荷,而这 3 个指标分别是人均耕地、第一产业占 三产比重、农用地结构,它们主要从农用地方面反映了土地利用经济效益,定名为“农用地 因子”。新疆的农用地主要分布在绿洲,农用地的利用程度可以反映新疆绿洲农业经济的发 展状况。 第二个主因子F2在X1、X 2、X 3、X10上有较大载荷,这五个指标分别是人均耕地、人均 建设用地、人均国内总产值、建设用地结构,他们反映了土地利用经济效益在建设用地利用 方面的实力,定名为“建设用地水平因子”。建设用地是影响土地利用结构、土地利用率、 土地可持续发展的重要因素之一,同时也是耕地的面积和保护的控制因素之一。 第三个主因子 F 3在 X 1,X 4,X 5、X 7上有较大载荷,这 4 个指标分别是农用地均产