
Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 w ww.o a s i s.x ju.e d u.c n atory of Oas 第六章AHP决策分析方法 AHP决策分析的基本原理与计算方法 AHP决策分析方法应用实例 U n ive r s it y
第六章 AHP决策分析方法 • AHP决策分析的基本原理与计算方法 • AHP决策分析方法应用实例

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www o a s i s x j u.e d u c n 一 ◇AHP决策分析法是一种定性与定量相结合的决 策分析方法;决策者对复杂系统的决策思维过 程模型化、数量化的过程。 ◇AHP方法特点: ①思路简单明了,它将决策者的思维过程条理 化、数量化,便于计算,容易被人们所接受;
◇AHP 决策分析法是一种定性与定量相结合的决 策分析方法;决策者对复杂系统的决策思维过 程模型化、数量化的过程。 ◇AHP方法特点: ① 思路简单明了,它将决策者的思维过程条理 化、数量化,便于计算,容易被人们所接受;

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 w ww.o a s i s.x ju.ed u.c n tory ②所需要的定量化数据较少,但对问题的 本质,问题所涉及的因素及其内在关系分析得 比较透彻,清楚。 ◇AHP决策分析法,常常被运用于多目标,多准 则,多要素,多层次的非结构化的复杂地理决 策问题,特别是战略决策问题的研究
◇ ② 所需要的定量化数据较少,但对问题的 本质,问题所涉及的因素及其内在关系分析得 比较透彻,清楚。 ◇AHP决策分析法,常常被运用于多目标,多准 则,多要素,多层次的非结构化的复杂地理决 策问题,特别是战略决策问题的研究
Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www o a s i s x j u e d u c n §6.1AHP决策分析的基本原理与 计算方法 >基本思想 AP决策分析方法的基本原理可以用一下的简单实例分析 来说明。假设有n个物体A1,A2,., An,它们的重量分 别记为W1,W2,.,Wn。 现将每个物体的重量两两进行比 较如下: 表6.1.1 A A Aa A W/W W/Wa W/W. A2 Wal W W2l W2 . W/W。 Aa W/W W/W: w/w
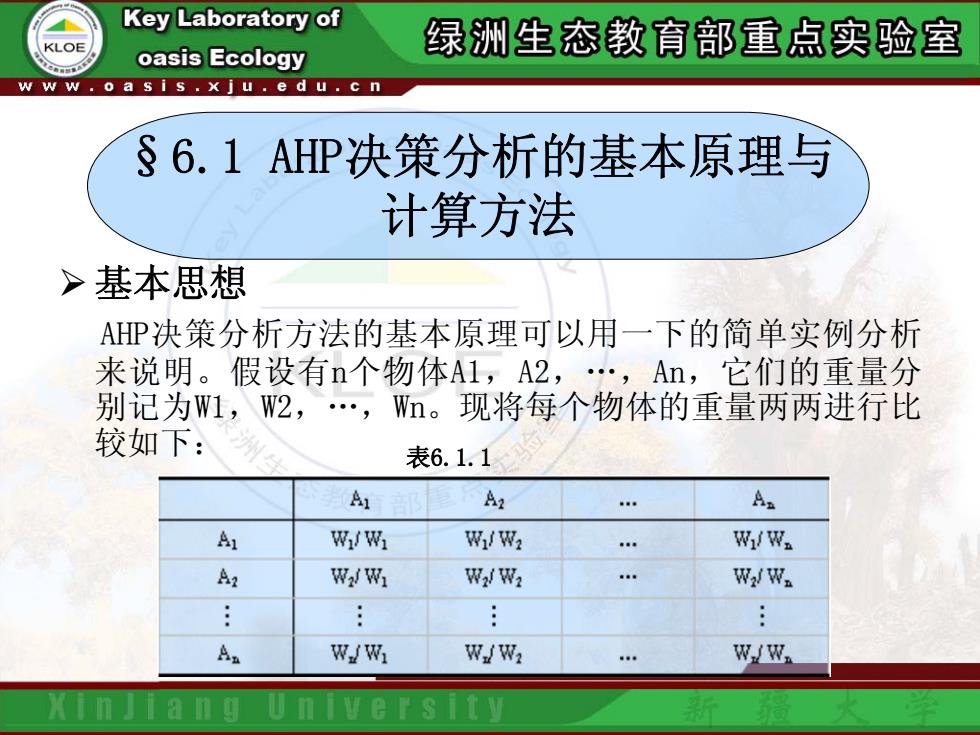
¾ 基本思想 AHP决策分析方法的基本原理可以用一下的简单实例分析 来说明。假设有n个物体A1,A2,.,An,它们的重量分 别记为W1,W2,.,Wn。现将每个物体的重量两两进行比 较如下: §6.1 AHP决策分析的基本原理与 计算方法 表6.1.1

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www.o a s i s.x ju.e d u.c n 矩阵形式: tory 若以矩阵来表示各物体的这种相互重量关系, W/WW/W : W/W w/WW/W, W/W A= (6.1.2) . : W/Ww/W: w/W A称为判断矩阵。 向量形式: 若取重量向量W=[W1,W2,.,Wn]T,则有: AW=n-W (6.1.3) W是判断矩阵A的特征向量,n是A的一个特征值。 Universitv
矩阵形式: 若以矩阵来表示各物体的这种相互重量关系, A= A称为判断矩阵。 向量形式: 若取重量向量W=[W1,W2,. , Wn]T,则有: AW=n•W W是判断矩阵A的特征向量,n是A的一个特征值。 ⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎝⎛ 2n1n nn 2212 n2 2111 n1 W/WW/WW/W W/WW/WW/W W/WW/WW/W M MM M MM (6.1.2) (6.1.3)

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www o a s i s x j u.e d u c n ratory of Oasis E >基本步骤 明确问题。弄清问题的范围,所包含的因素,各因 素之间的关系等,以便尽量掌握充分的信息。 建立层次结构模型。将问题所含的要素按照最高层 (目标层),若干中间层(准则层)以及最低层 (措施层)的形式排列起来
¾ 基本步骤 • 明确问题。弄清问题的范围,所包含的因素,各因 素之间的关系等,以便尽量掌握充分的信息。 • 建立层次结构模型。将问题所含的要素按照最高层 (目标层),若干中间层(准则层)以及最低层 (措施层)的形式排列起来
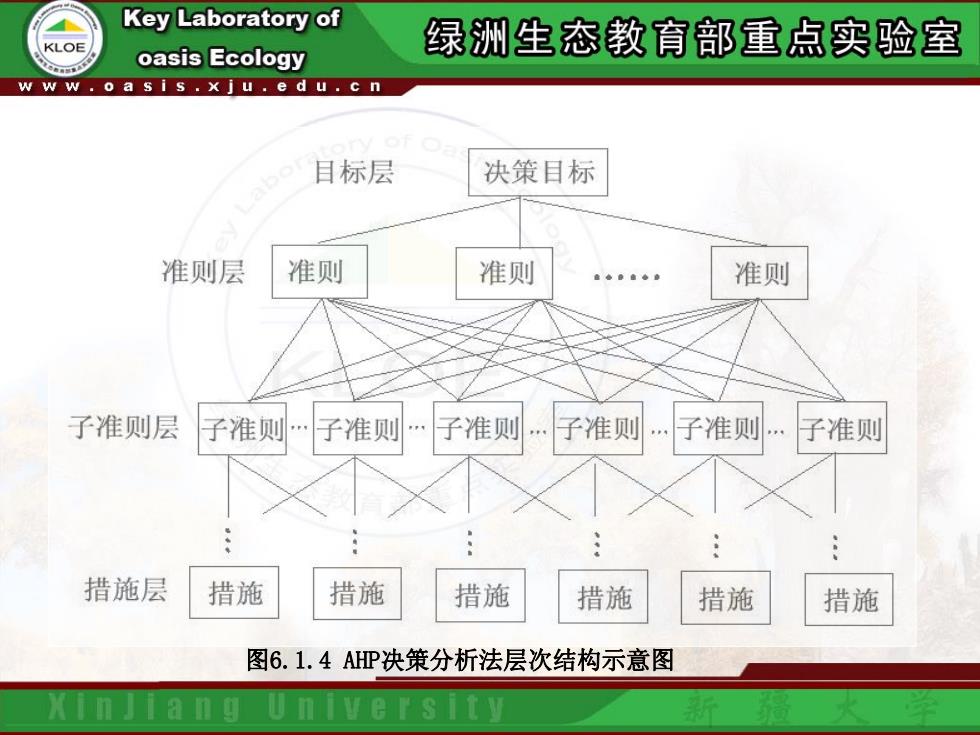
Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 w ww.o a s i s.x ju.e d u.c n 目标层 决策目标 准则层 准则 准则 准则 子准则层 子准则子准则.子准则.子准则 .子准则.子准则 措施层 措施 措施 措施 措施 措施 措施 图6.1.4AHP决策分析法层次结构示意图
图6.1.4 AHP决策分析法层次结构示意图

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www o a s i s x j u e d u c n 构造判断矩阵。atory of Oa ①判断矩阵表示针对上一层次中的某元素而言,评定该 层次中各有关元素相对重要性的状况。 表6.1.5 A Bi B2 B2 B bu b12 . bia B2 b21 b22 b2a Bn ba bi b go ②b表示对于Ak而言,元素B:对B,的相对重要性的判断值。 b一般取1,3,5,7, 9等5个等级标度
• 构造判断矩阵。 ① 判断矩阵表示针对上一层次中的某元素而言,评定该 层次中各有关元素相对重要性的状况。 ② bij表示对于Ak而言,元素Bi对Bj的相对重要性的判断值。 bij一般取1,3,5,7,9等5个等级标度。 表6.1.5

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 www o a s i s x j u.e d u c n ③对于任何判断矩阵都应满足 bn= as c(1, j=1,2,.,n) b b (6.1.6) 一 般而言,判断矩阵的数值是根据数据资料、专家意见和 分析者的认识,加以平衡后给出的。 如果判断矩阵存在关系: bij b i,j,k=1,2,3,.’n b水 (6.1.7) 则称它具有完全一致性。 为了考察AHP决策分析方法得出的结果是否基本合理,需要 对判断矩阵进行一致性检验。 Universitv
③ 对于任何判断矩阵都应满足 (1,j=1,2,.,n) ④ 一般而言,判断矩阵的数值是根据数据资料、专家意见和 分析者的认识,加以平衡后给出的。 ⑤ 如果判断矩阵存在关系: bij= (i,j,k=1,2,3,.,n) 则称它具有完全一致性。 ⑥ 为了考察AHP决策分析方法得出的结果是否基本合理,需要 对判断矩阵进行一致性检验。 ⎪ ⎩ ⎪ ⎨ ⎧ = = ji ij ii b b b 1 1 jk ik b b (6.1.6) (6.1.7)

Key Laboratory of KLOE oasis Ecology 绿洲生态教育部重点实验室 o a s i s x j u.e d u c n 层次单排序。tory of o. ★任务:计算判断矩阵的特征根和特征向量。 ① 对于判断矩阵B,计算满足: BW=入maxW (6.1.8) 的特征根和特征向量。 入max为B的最大特征根,W为对应于入max的 正规化特征向量,W的分量W,就是对应元素单排 序的权重值
• 层次单排序。 ★ 任务:计算判断矩阵的特征根和特征向量。 ① 对于判断矩阵B,计算满足: BW=λmaxW 的特征根和特征向量。 λmax为B的最大特征根,W为对应于λmax的 正规化特征向量,W的分量Wi就是对应元素单排 序的权重值。 (6.1.8)