
Outline of dynamic games of complete information Dynamic games of complete information ■ Extensive-form representation Dynamic games of complete and perfect information ■Game tree Subgame-perfect Nash equilibrium ■Backward induction ■Applications Dynamic games of complete and imperfect information ■More applications ■Repeated games
Outline of dynamic games of complete information ◼ Dynamic games of complete information ◼ Extensive-form representation ◼ Dynamic games of complete and perfect information ◼ Game tree ◼ Subgame-perfect Nash equilibrium ◼ Backward induction ◼ Applications ◼ Dynamic games of complete and imperfect information ◼ More applications ◼ Repeated games 2
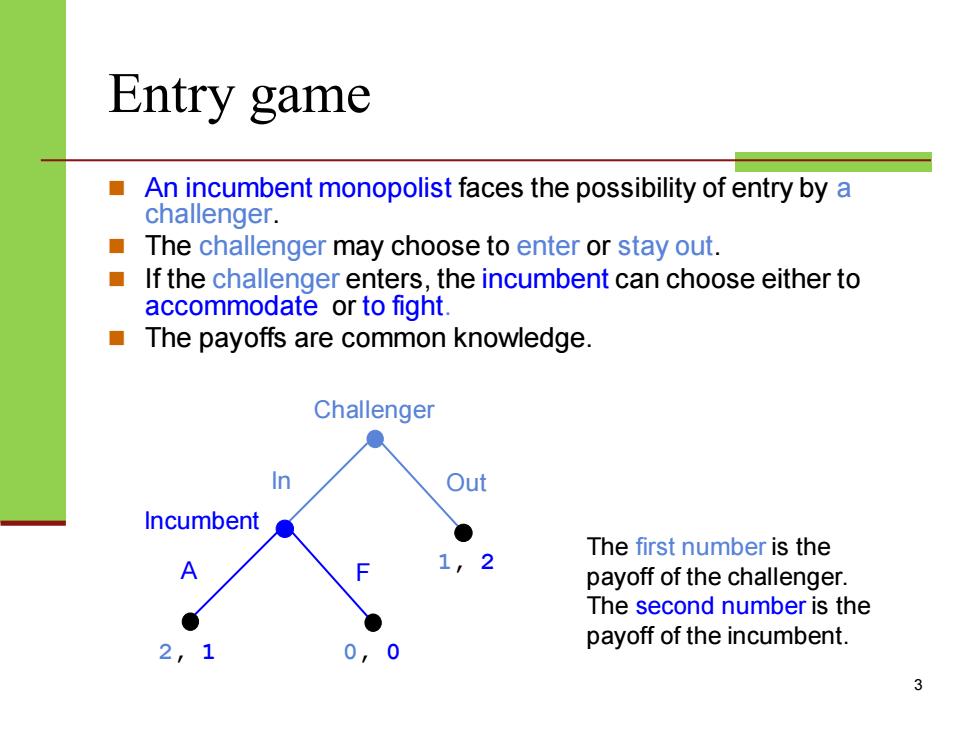
Entry game An incumbent monopolist faces the possibility of entry by a challenger. The challenger may choose to enter or stay out. If the challenger enters,the incumbent can choose either to accommodate or to fight. The payoffs are common knowledge. Challenger In Out Incumbent The first number is the 1 2 payoff of the challenger. The second number is the 2, 0,0 payoff of the incumbent. 3
Entry game ◼ An incumbent monopolist faces the possibility of entry by a challenger. ◼ The challenger may choose to enter or stay out. ◼ If the challenger enters, the incumbent can choose either to accommodate or to fight. ◼ The payoffs are common knowledge. 3 Challenger In Out Incumbent A F 1, 2 2, 1 0, 0 The first number is the payoff of the challenger. The second number is the payoff of the incumbent
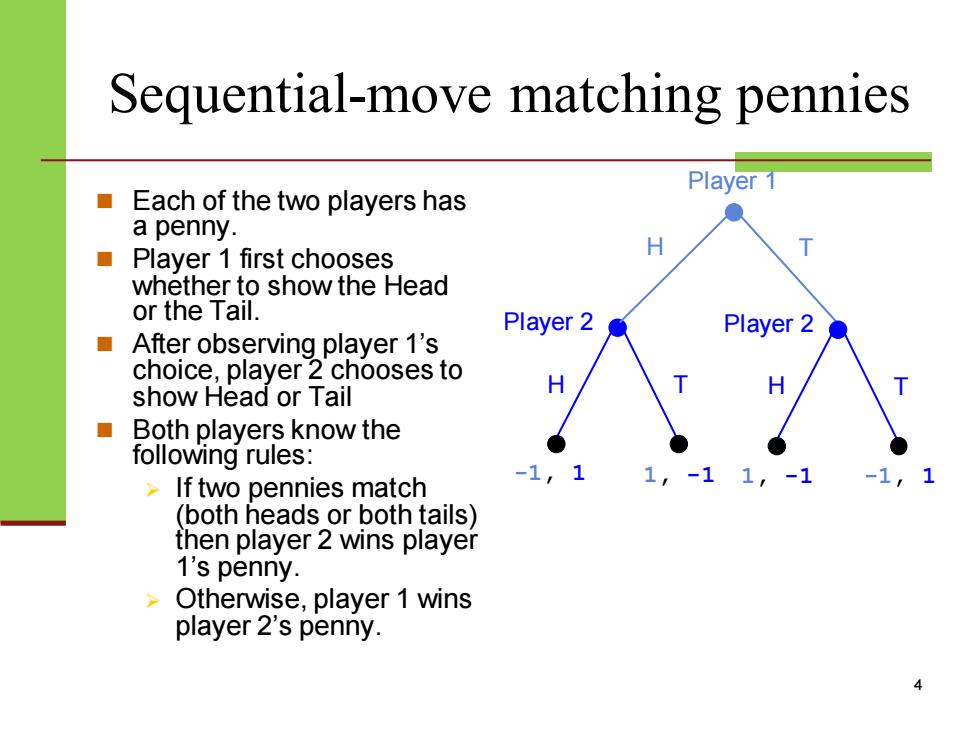
Sequential-move matching pennies Player 1 ■ Each of the two players has a penny. Player 1 first chooses whether to show the Head or the Tail. Player 2 Playe After observing player 1's choice,player 2 chooses to show Head or Tail Both players know the following rules: If two pennies match (both heads or both tails) then player 2 wins player 1's penny. Otherwise,player 1 wins player 2's penny
Sequential-move matching pennies ◼ Each of the two players has a penny. ◼ Player 1 first chooses whether to show the Head or the Tail. ◼ After observing player 1’s choice, player 2 chooses to show Head or Tail ◼ Both players know the following rules: ➢ If two pennies match (both heads or both tails) then player 2 wins player 1’s penny. ➢ Otherwise, player 1 wins player 2’s penny. 4 Player 1 Player 2 H T -1, 1 1, -1 H T Player 2 H T 1, -1 -1, 1

Dynamic (or sequential-move)games of complete information ■A set of players Who moves when and what action choices are available? What do players know when they move? Players'payoffs are determined by their choices. All these are common knowledge among the players
Dynamic (or sequential-move) games of complete information ◼ A set of players ◼ Who moves when and what action choices are available? ◼ What do players know when they move? ◼ Players’ payoffs are determined by their choices. ◼ All these are common knowledge among the players. 5

Definition:extensive-form representation The extensive-form representation of a game specifies: the players in the game when each player has the move > what each player can do at each of his or her opportunities to move what each player knows at each of his or her opportunities to move the payoff received by each player for each combination of moves that could be chosen by the players 6
Definition: extensive-form representation ◼ The extensive-form representation of a game specifies: ➢ the players in the game ➢ when each player has the move ➢ what each player can do at each of his or her opportunities to move ➢ what each player knows at each of his or her opportunities to move ➢ the payoff received by each player for each combination of moves that could be chosen by the players 6

Dynamic games of complete and perfect information ■Perfect information -All previous moves are observed before the next move is chosen. >A player knows Who has moved What before she makes a decision
Dynamic games of complete and perfect information ◼ Perfect information ➢ All previous moves are observed before the next move is chosen. ➢ A player knows Who has moved What before she makes a decision 7
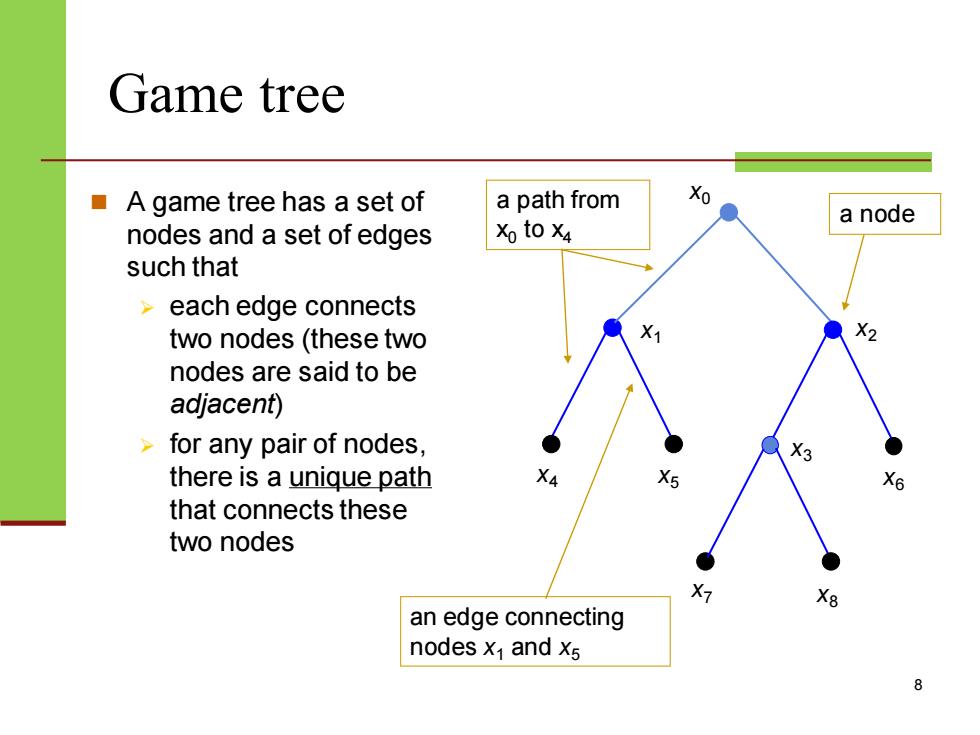
Game tree ■ A game tree has a set of a path from Xo a node nodes and a set of edges Xo to x4 such that > each edge connects two nodes (these two X2 nodes are said to be adjacent) for any pair of nodes, X3 there is a unique path X6 that connects these two nodes X8 an edge connecting nodes x1 and x5
Game tree ◼ A game tree has a set of nodes and a set of edges such that ➢ each edge connects two nodes (these two nodes are said to be adjacent) ➢ for any pair of nodes, there is a unique path that connects these two nodes 8 x0 x1 x2 x3 x4 x5 x6 x7 x8 a node an edge connecting nodes x1 and x5 a path from x0 to x4
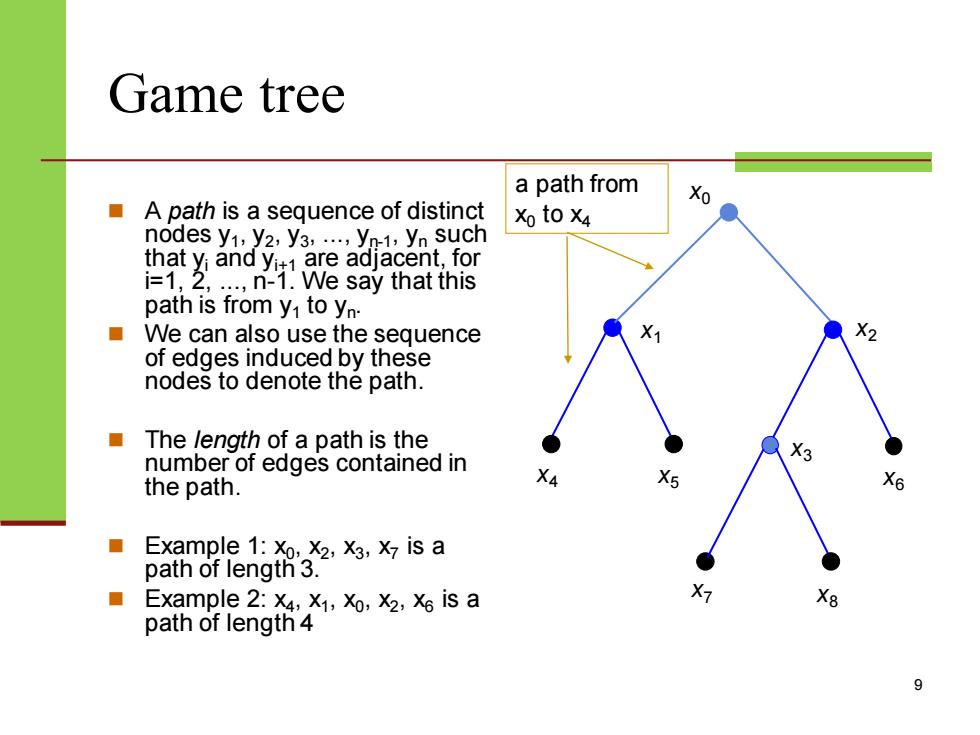
Game tree a path from A path is a sequence of distinct Xo Xo to x4 nodes y1,y2,y3,...,yn-1,yn such that yi and yit1 are adjacent,for i=1,2,...n-1.We say that this path is from y1 to yn. We can also use the sequence X2 of edges induced by these nodes to denote the path. The length of a path is the number of edges contained in the path. X6 Example 1:Xo,X2,X3,X7 is a path of length 3. Example 2:X4,X1,Xo,X2,X6 is a X7 path of length 4
Game tree ◼ A path is a sequence of distinct nodes y1 , y2 , y3 , ..., yn-1 , yn such that yi and yi+1 are adjacent, for i=1, 2, ..., n-1. We say that this path is from y1 to yn . ◼ We can also use the sequence of edges induced by these nodes to denote the path. ◼ The length of a path is the number of edges contained in the path. ◼ Example 1: x0 , x2 , x3 , x7 is a path of length 3. ◼ Example 2: x4 , x1 , x0 , x2 , x6 is a path of length 4 9 x0 x1 x2 x3 x4 x5 x6 x7 x8 a path from x0 to x4
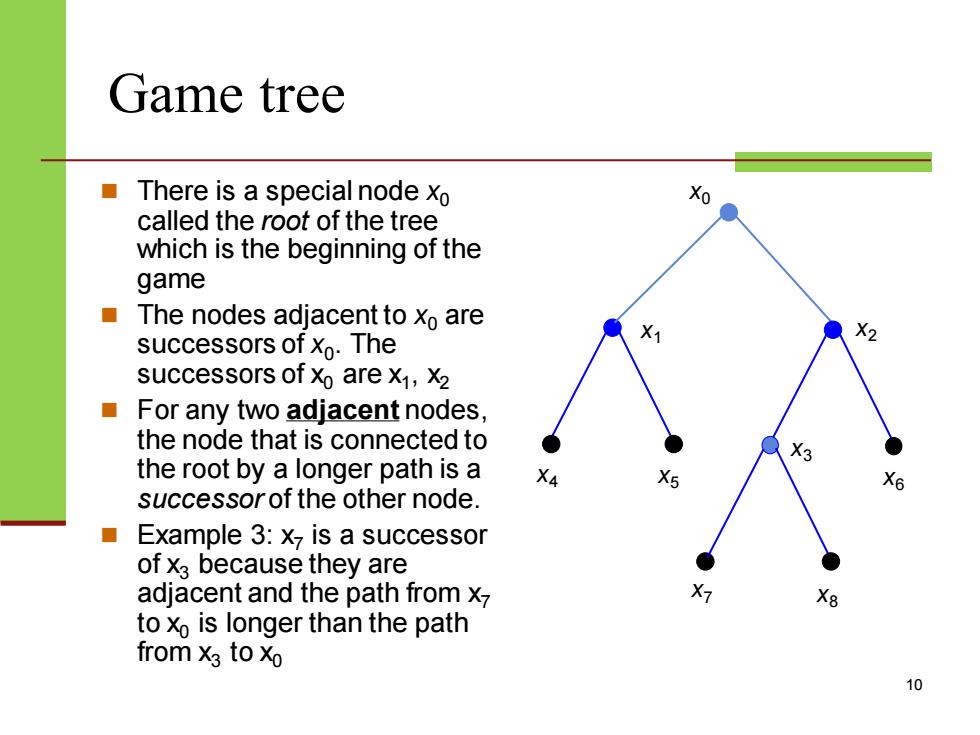
Game tree There is a special node xo Xo called the root of the tree which is the beginning of the game The nodes adjacent to xo are successors of xo.The successors of xo are x1,X2 For any two adjacent nodes, the node that is connected to the root by a longer path is a X4 X6 successor of the other node. Example 3:x is a successor of x3 because they are adjacent and the path from x X8 to xo is longer than the path from x3 to Xo 6
Game tree ◼ There is a special node x0 called the root of the tree which is the beginning of the game ◼ The nodes adjacent to x0 are successors of x0 . The successors of x0 are x 1 , x2 ◼ For any two adjacent nodes, the node that is connected to the root by a longer path is a successor of the other node. ◼ Example 3: x7 is a successor of x3 because they are adjacent and the path from x7 to x0 is longer than the path from x3 to x0 10 x0 x 1 x2 x3 x4 x5 x6 x7 x8
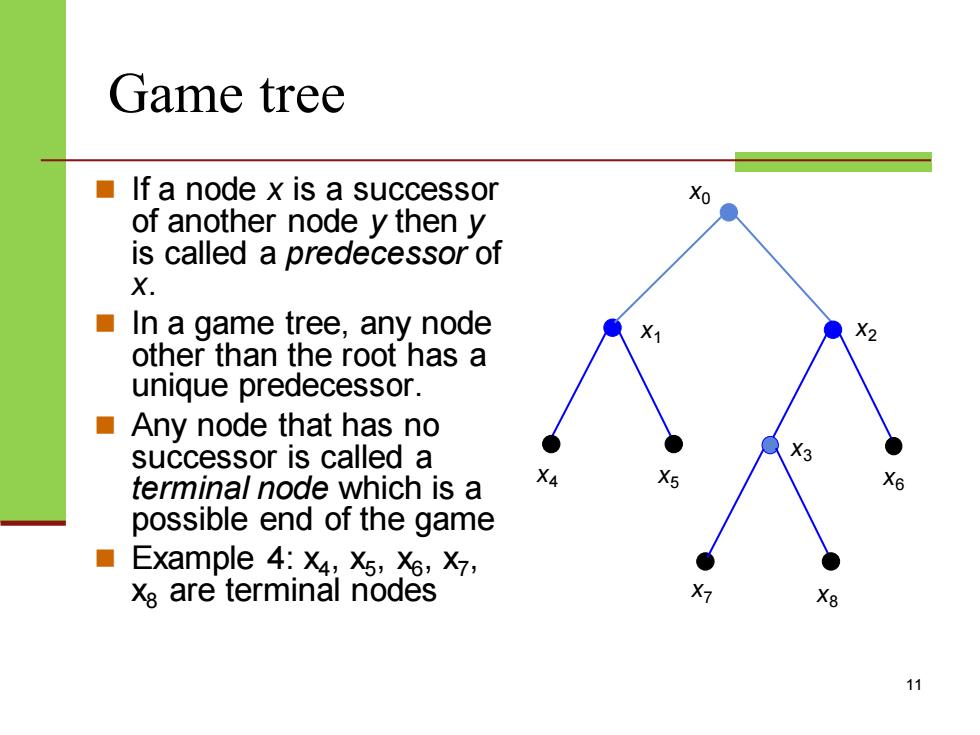
Game tree If a node x is a successor Xo of another node y then y is called a predecessor of X. In a game tree,any node X2 other than the root has a unique predecessor. ■Any node that has no successor is called a terminal node which is a X4 X5 X6 possible end of the game ■ Example 4:X4:X5,X6,X7, Xs are terminal nodes X7 X8 11
Game tree ◼ If a node x is a successor of another node y then y is called a predecessor of x. ◼ In a game tree, any node other than the root has a unique predecessor. ◼ Any node that has no successor is called a terminal node which is a possible end of the game ◼ Example 4: x4 , x5 , x6 , x7 , x8 are terminal nodes 11 x0 x1 x2 x3 x4 x5 x6 x7 x8