
第二章线性规划的基本性质 §1 标准形式与图解法 §2基本性质
第二章 线性规划的基本性质 §1 标准形式与图解法 §2 基本性质

线性规划(Linear Programming,简称LP) 数学规划的一个重要分支,是数学规划中研究较早、发 展较快、理论上较成熟和应用上极为广泛的一个分支。 1947年G.B.Dantzig提出了一般线性规划问题求解 的方法—单纯形法之后, 线性规划的理论与应用都得 到了极大的发展。 60年来,随着计算机的发展, 线性规划已广泛应用 于工业、农业、 商业、交通运输、 经济管理和国防等各 个领域,成为现代化管理的有力工具之
线性规划(Linear Programming,简称LP) 数学规划的一个重要分支,是数学规划中研究较早、发 展较快、理论上较成熟和应用上极为广泛的一个分支。 1947年G.B. Dantzig提出了一般线性规划问题求解 的方法——单纯形法之后,线性规划的理论与应用都得 到了极大的发展。 60年来,随着计算机的发展,线性规划已广泛应用 于工业、农业、商业、交通运输、经济管理和国防等各 个领域,成为现代化管理的有力工具之一
e.g.1资源的合理利用问题 某工厂在下一个生产周期内生产甲、乙两种产品, 要消耗A、B两种资源,已知每件产品对这两种资源 的 消耗,这两种资源的现有数量一体立口一本阳王 表1 润如表1 同:茹何安排生产计划 产品 资源 甲 乙 库存量 使得既能充分利用现有资 A 1 3 60 B 1 1 40 源又使总利润最大? 单件利润 15 25
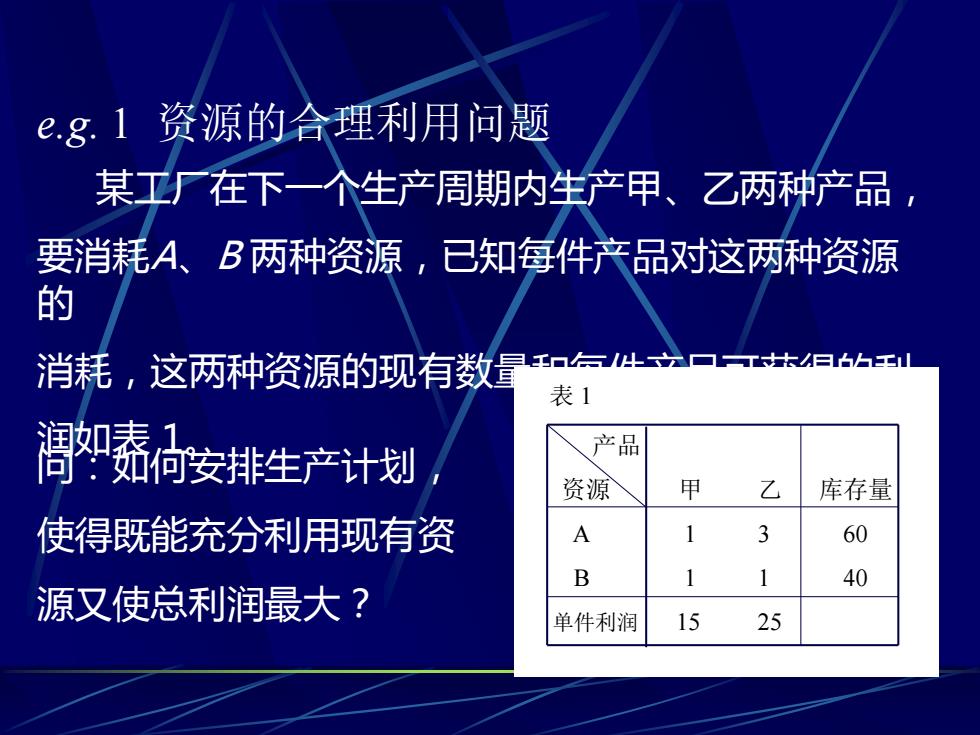
e.g. 1 资源的合理利用问题 问:如何安排生产计划, 使得既能充分利用现有资 源又使总利润最大? 表 1 产品 资源 甲 乙 库存量 A 1 3 60 B 1 1 40 单件利润 15 25 某工厂在下一个生产周期内生产甲、乙两种产品, 要消耗A、B 两种资源,已知每件产品对这两种资源 的 消耗,这两种资源的现有数量和每件产品可获得的利 润如表 1

决策变量 解:设1,x2为下一个生 表1 产周期产品甲和乙的产量: 产品 约束条件: 资源 甲 乙 库存量 A 1 3 60 x1+3x2≤60 B 1 1 40 x1+x2≤40 单件利润 15 25 x1,x2≥0 目标函数: max z=15x1+25x2 s.t. x1+3x2≤60 z=15x1+25x2 x1+x2≤40 Subject to x1,x2≥0
max z = 15x1 +25x2 s.t. x1 + 3x2 ≤ 60 x1 + x2 ≤ 40 x1,x2 ≥ 0 解 : 设 x1,x2 为下一个生 产周期产品甲和乙的产量; 约束条件: Subject to x1 + 3x2 ≤ 60 x1 + x2 ≤ 40 x1,x2 ≥ 0 目标函数: z = 15 x1 +25 x2 表 1 产品 资源 甲 乙 库存量 A 1 3 60 B 1 1 40 单件利润 15 25 决策变量
e.g2营养问题 假定在市场上可买到B,B2,Bnn种食品,第i种 食品的单价是c,另外有m种营养A,A2,…Am。设B, 内含有A,种营养数量为a,(i1~mj1~n),又知人们每 天对A,营养的最少 表2 需要量为b,。见表2: 食品 最少 试在满足营养要 营养 BI B2 Bn 需要量 求的前提下,确定食 A a11 a12 aIn bi A a21 a22 a2n b2 品的购买量,使食品 Am aml am2 amn bm 的总价格最低 单价 C1 C2 Cn
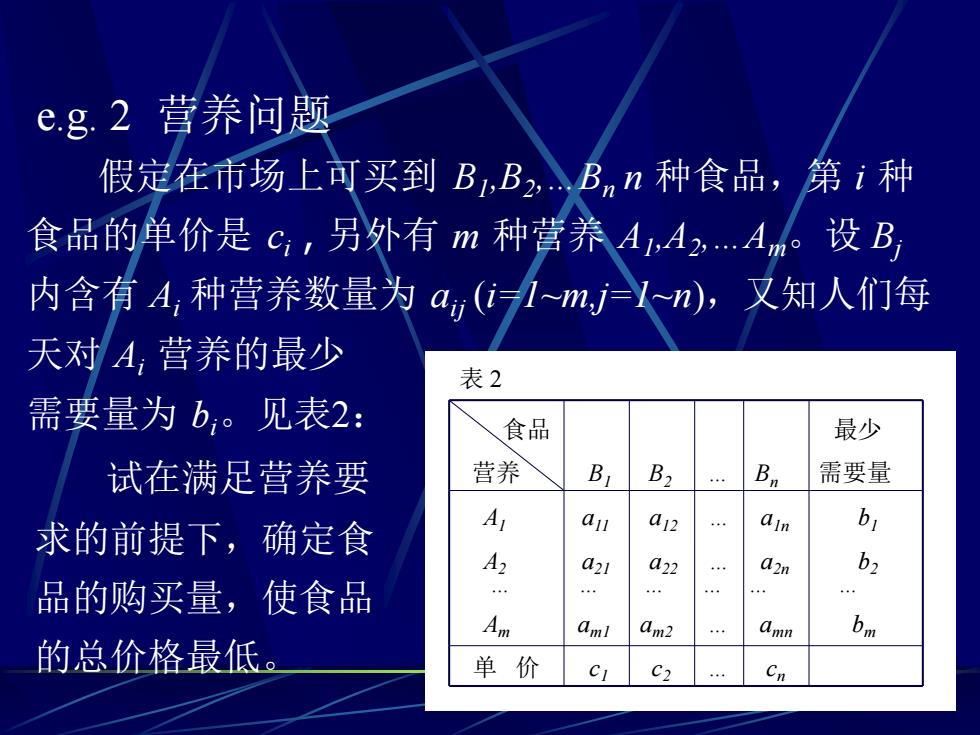
e.g. 2 营养问题 假定在市场上可买到 B1 ,B2 ,…Bn n 种食品,第 i 种 食品的单价是 ci , 另外有 m 种营养 A1 ,A2 ,…Am。设 Bj 内含有 Ai 种营养数量为 aij (i=1~m,j=1~n),又知人们每 天对 Ai 营养的最少 需要量为 bi。见表2: 表 2 食品 最少 营养 B1 B2 … Bn 需要量 A1 a11 a12 … a1n b1 A2 a21 a22 … a2n b2 … … … … … … Am am1 am2 … amn bm 单 价 c1 c2 … cn 试在满足营养要 求的前提下,确定食 品的购买量,使食品 的总价格最低

解: 表2 设x,为购买食 食品 最少 品B,的数量(j=1,2, 营养 Bi B2 Bn 需要量 A all a12 aln bi A2 a21 d22 a2n b2 Am aml am2 amn bm 单价 C1 min C2 Cn s.t. 24x,2b (i=1,2,…,m 0<x;<lj x20J=1,2.,n)
表 2 食品 最少 营养 B1 B2 … Bn 需要量 A1 a11 a12 … a1n b1 A2 a21 a22 … a2n b2 … … … … … … Am am1 am2 … amn bm 单 价 c1 c2 … cn 解 : 设 xj 为购买食 品 Bj 的数量 ( j=1,2, …,n ) (i = 1,2,…,m) xj ≥0 (j = 1,2,…,n) 0≤ xj ≤l j 1 min n j j j z c x = = 1 . . n ij j i j s t a x b =

Note: 1、善于抓住关键因素 ,忽略对系统影响不大的因素; 2、可以把一个大系统合理地分解成个子系统处理。 三个基本要素: 1、决策变量 x≥0 2、约束条件 组决策变量的线性等式或不等式 3、目标函数一一决策变量的线性函数
三个基本要素: Note: 1、善于抓住关键因素,忽略对系统影响不大的因素; 2、可以把一个大系统合理地分解成 n 个子系统处理。 1、决策变量 xj≥0 2、约束条件 —— 一组决策变量的线性等式或不等式 3、目标函数 —— 决策变量的线性函数

2.1标准形式与图解法 线性规划问题的一般形式: min(ax)z=c+Cx2+… S.t. a1x1+a1zX3++a1mxn(或,≥)b, a2x1+a22x3+.十a2n≤(或-入2)b2 amX1+amX3+…十Amn≤(或-,≥)bm x,≥0=1,2,.,n》 其中a,b,、C(i=1,2,,m;j=1,2,,n)为已知 常数
min(max)z = c1 x1 + c2 x2 + … + cn xn s.t. a11x1+ a12x2+ … + a1n xn≤(或=,≥)b1 a21x1+ a22x2+ … + a2n xn ≤(或=,≥)b2 … … am1 x1 + am2 x2+ … + amnxn ≤(或=,≥)bm xj ≥ 0 (j = 1,2,…,n) 其中aij、bi、cj(i = 1,2,…,m;j = 1,2,…,n)为已知 常数 线性规划问题的一般形式: 2.1 标准形式与图解法

§2.1.1标准形式 特点: 线性规划问题的标准形式: 1、目标函数为极 min 9=Cx1+CX2t…+CXm 小化: 2、除决策变量的 S.t. aux1+a1xx2+ainn _bi 非负约束外,所有 a2x1+a2zx2+.十a2mYn =b2 的约束条件都是等 式,且右端常数均 amX1+am2X3+…十Amn=bm 为非负; x≥0=1,2,.,n) 3、所有决策变量 均非负。 b,≥0(1=1,2,,m)
线性规划问题的标准形式: min z = c1 x1 + c2 x2 + … + cn xn s.t. a11x1+ a12x2+ … + a1n xn = b1 a21x1+ a22x2+ … + a2n xn = b2 … … am1 x1+ am2 x2+ … + amnxn = bm xj ≥ 0 (j = 1,2,…,n) bi ≥ 0 (i = 1,2,…,m) 特点: 1、目标函数为极 小化; 2、除决策变量的 非负约束外,所有 的约束条件都是等 式,且右端常数均 为非负; 3、所有决策变量 均非负。 §2.1.1 标准形式

如何转化为标准形式? 1、目标函数为求极大值,即为 maxz= cx, j=l 因为求maxz等价于求min(-z),令z=-z, 即化为: min=x xn+1≥0 松弛变量 2 约束条件为不等式 n ax,≤b Xn+l j=1 aux,≥b, 如何处理?
如何转化为标准形式? 1、目标函数为求极大值,即为: max 1 。 n j j j z c x = = ' 1 min n j j j z c x = = − 因为求 max z 等价于求 min (-z),令 z’ = - z, 即化为: 2、约束条件为不等式, = + + = n j ij j n bi a x x 1 1 = n j aij x j bi 1 = n j aij x j bi 1 xn+1 ≥ 0 松弛变量 如何处理?