
Chapter 6 Jointly Distributed Random Variables
Chapter 6 Jointly Distributed Random Variables

6.1 Joint distribution functions For any two random variables X and Y.the joint cumulative probability distribution function of X and Y by F(a,b)=P(X≤a,Y≤b)-o<a,b<o
6.1 Joint distribution functions var , (,) ( , ) , joint cumulative probability distribution For any two random iables X and Y f the u of X and Y by F ab P X aY b nct a b ion = ≤ ≤ −∞< <∞
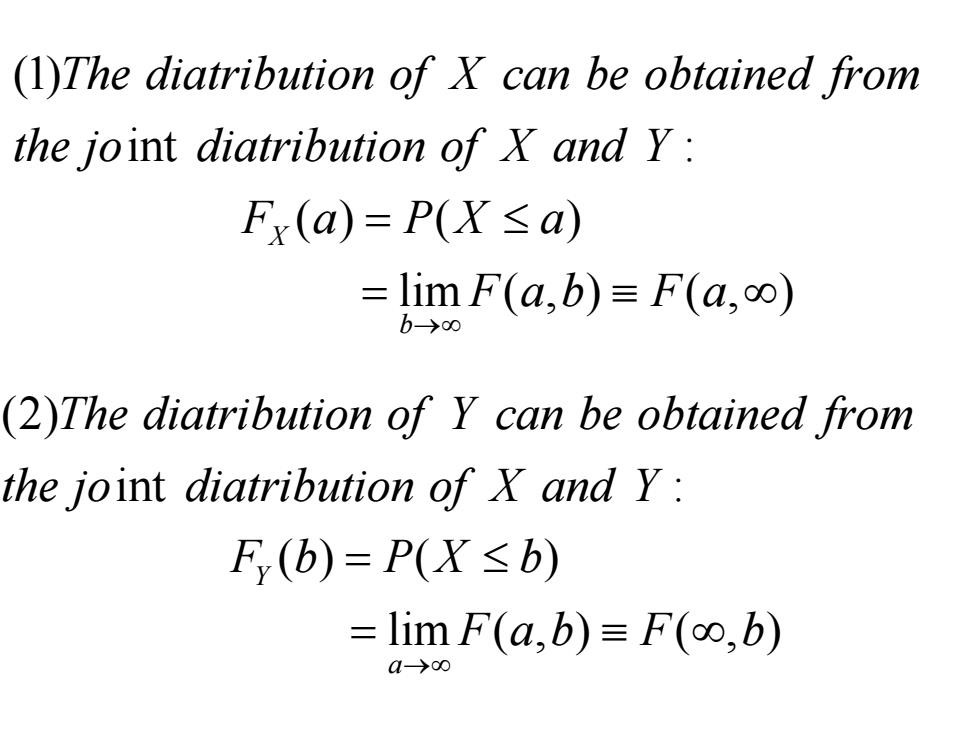
(1)The diatribution of X can be obtained from the joint diatribution of X and y: Fx(a)=P(X≤a) =limF(a,b)≡F(a,oo) b→00 (2)The diatribution of Y can be obtained from the joint diatribution of X and Y: F,(b)=P(X≤b) =limF(a,b)≡F(oo,b) a-→00
(1) int : () ( ) lim ( , ) ( , ) X b The diatribution of X can be obtained from the jo diatribution of X and Y F a PX a F ab F a →∞ = ≤ = ≡∞ (2) int : () ( ) lim ( , ) ( , ) Y a The diatribution of Y can be obtained from the jo diatribution of X and Y F b PX b F ab F b →∞ = ≤ = ≡∞

Notice P(a1<X≤a2,b<Y≤b) =F(a2,b2)+F(a,b)-F(a,b)-F(a2,b) Whennever a <a,b<b2
1 21 2 2 2 11 12 21 1 21 2 ( ,) (,) (,) (,) (,) , . Pa X a b Y b Fa b Fab Fab Fa b Whennever a a b b < ≤ <≤ = +−− < < Notice

Discrete random variables Define the joint probability mass function of X and Y by p(x,y)=P(X=x,Y=y) The probability mass function of X can be obtained from p(x,y)by px(x)=P(X=x) =∑p(x,y) y:p(x,y)>0
Discrete random variables (, ) { , } Define the joint probabi of X and Y by pxy lity mass functio PX x y n = = = Y :(,)0 ( , ) () { } (, ) X yp xy The probability mass function of X can be obtained from p x y by p x PX x pxy > = = = ∑

Example 1a Suppose that 3 balls are random selected from an urn containing 3 red,4 white,and 5 blue balls. If we let X and Y denote,respectively,the number of red and white balls chosen.Calculate the joint probability mass funtion of X and Y
Example 1a 3 3 , 4 , 5 . , , . int Suppose that balls are random selected from an urn containing red white and blue balls If we let X and Y denote respectively the number of red and white balls chosen Calculate the jo probability mass funtion of X and Y

We say that X and Y are jointly continuous if there exists a funtion f(x,y)defined for all real x and y,having the property that for every set C of pairs of real numbers P((X,Y)EC)=f(x,y)dxdy (X,Y)∈C The function f(x,y)is called the joint probability density function of X and y
( , ) , {( , ) } ( , ) We say that X and Y are if there exists a funtion f x y defined for all real x and y having the property that for every set C of pairs of re jointly c al numbers P XY C f ontinuo xy x u d s ∈ = d ( ,) ( , ) . XY C joint probability densit y The fun y func ction f tio x y is called t n he of X and Y ∈ ∫∫

Notice (1)If A and B are any sets of real numbers, then P{X∈A,Y∈B}=JeJ,f(x,y)dd (2)F(a,b)=f(x,y)dxdy (3)f(a,b)= _F(a.b) Eadb whenever the partial derivatives are defined
Notice (2) ( , ) ( , ) a b F a b f x y dxdy −∞ −∞ = ∫ ∫ 2 (3) ( , ) ( , ) . f ab F ab a b whenever the partial derivatives are defined ∂ = ∂ ∂ (1) , { , } ( , ) B A If A and B are any sets of real numbers then P X A Y B f x y dxdy ∈ ∈= ∫ ∫

(4)If X and Y are jointly continuous,they are individually continuous,and their probability density functions can be obtained as follows: PXeA=∫Jfx,y)dd =了Jfr(xah where fx(x)=f(x.yrdy
(4) , , : { } (, ) A If X and Y are jointly continuous they are individually continuous and their probability density functions can be obtained as follows P X A f x y dydx ∞ −∞ ∈ = ∫ ∫ () () (, ) . X A X f x dx where f x f x y dy ∞ −∞ = = ∫ ∫

Example 1a The joint density funtion of X and Y is given by m2ee”01,Y<1(b)P(X<Y (c)PX <a
Example 1a 2 int 2 0 ,0 (, ) 0 ( ) { 1, 1} ( ) { } () { } x y The jo density funtion of X and Y is given by ee x y f xy otherwise Compute a P X Y b P X Y cPX a − − < < <