
目录》 01 导数的几何意义 CONTENTS 02 几种特殊的共形映照
目 录 CONTENTS 01 导数的几何意义 02 几种特殊的共形映照

01 PART 导数的几何意义
导数的几何意义 01 PART

导数与反函数 对实变量函数f(x),若f(x)连续可导且f'(xo)≠0,则f(x)局 部单调,从而局部存在反函数.反之不成立!(即f(x)局部单 调,但f'(xo)有可能为零,例如f(x)=x3) 。 对复变量函数f(z),若f(z)解析且f'(zo)≠0,则局部存在反函 数.反之也成立!
导数与反函数 • 对实变量函数 𝑓(𝑥),若 𝑓(𝑥) 连续可导且 𝑓′ 𝑥0 ≠ 0,则 𝑓(𝑥) 局 部单调,从而局部存在反函数. 反之不成立!(即 𝑓(𝑥) 局部单 调,但 𝑓′ 𝑥0 有可能为零,例如 𝑓 𝑥 = 𝑥 3) • 对复变量函数 𝑓(𝑧),若 𝑓(𝑧) 解析且 𝑓′ 𝑧0 ≠ 0,则局部存在反函 数. 反之也成立!

例子 考虑f(z)=z3,其导数f(z)=3z2. 当z≠0时,f'(z)≠0,总可以取到z的充分小的邻域U,使得 在U中,任意两个数的幅角之差都小于?,这样在U内只要a≠ 2,就有f(21)≠f(22),即在U内f可定义反函数. 当z=0时,f'(0)=0,此时无论如何取z的邻域U,在U中, 总能找到两个数21,22(事实上可以找到无穷多对这样的数), 两数的模相同且幅角之差恰为;,这样就有f(2)=f(22),即在 0的任何邻域内f都不可定义反函数
例子 考虑 𝑓 𝑧 = 𝑧 3,其导数 𝑓′ 𝑧 = 3𝑧 2. • 当 𝑧 ≠ 0 时,𝑓′ 𝑧 ≠ 0,总可以取到 𝑧 的充分小的邻域 𝑈,使得 在 𝑈 中,任意两个数的幅角之差都小于 π 3 ,这样在 𝑈 内只要 𝑧1 ≠ 𝑧2,就有 𝑓(𝑧1) ≠ 𝑓(𝑧2),即在 𝑈 内 𝑓 可定义反函数. • 当 𝑧 = 0 时,𝑓′ 0 = 0,此时无论如何取 𝑧 的邻域 𝑈,在 𝑈 中, 总能找到两个数 𝑧1,𝑧2(事实上可以找到无穷多对这样的数), 两数的模相同且幅角之差恰为 π 3,这样就有 𝑓 𝑧1 = 𝑓(𝑧2),即在 0 的任何邻域内 𝑓 都不可定义反函数.
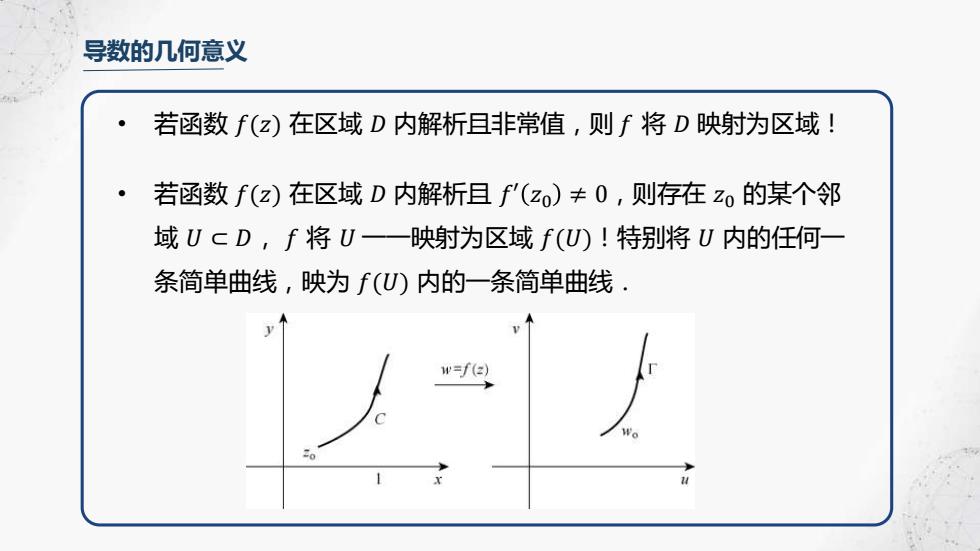
导数的几何意义 若函数f(z)在区域D内解析且非常值,则f将D映射为区域! 若函数f(z)在区域D内解析且f'(zo)≠0,则存在zo的某个邻 域UcD,f将U一映射为区域f(U!特别将U内的任何一 条简单曲线,映为f(U)内的一条简单曲线. w=f(2)
导数的几何意义 • 若函数 𝑓(𝑧) 在区域 𝐷 内解析且非常值,则 𝑓 将 𝐷 映射为区域! • 若函数 𝑓(𝑧) 在区域 𝐷 内解析且 𝑓′ 𝑧0 ≠ 0,则存在 𝑧0 的某个邻 域 𝑈 ⊂ 𝐷, 𝑓 将 𝑈 一一映射为区域 𝑓(𝑈)!特别将 𝑈 内的任何一 条简单曲线,映为 𝑓(𝑈) 内的一条简单曲线.

导数的几何意义(续) 考虑U内过z0的简单参数曲线C:z(t),其中0≤t≤e,z(0)= 2o·f(C)为C在映射f下的像曲线,其参数方程为f(z(t),其 中f(z(0)=f(zo)=wo· C在z0的切向量为立=z(0),物理意义为以该参数方程描述的运 动质点,在z的速度,f(C)在wo的切向量为元='(zo)z(0), 物理意义运动质点在映射f下的对应点,在wo的速度, 比较两个速度的大小和方向,发现 wl=If'(zo).,Argw=Arg f'(zo)+Arg If'(zo)川为速度大小变化的比率,Agf'(zo)为速度方向转动的角度
导数的几何意义(续) • 考虑 𝑈 内过 𝑧0 的简单参数曲线 𝐶: 𝑧 𝑡 ,其中 0 ≤ t ≤ ϵ,𝑧 0 = 𝑧0. 𝑓(𝐶) 为 𝐶 在映射 𝑓 下的像曲线,其参数方程为 𝑓(𝑧 𝑡 ),其 中 𝑓 𝑧 0 = 𝑓 𝑧0 = 𝑤0. • 𝐶 在 𝑧0 的切向量为 𝑣 Ԧ = 𝑧′ 0 ,物理意义为以该参数方程描述的运 动质点,在 𝑧0 的速度,𝑓(𝐶) 在 𝑤0 的切向量为 𝑤 = 𝑓′(𝑧0)𝑧′ 0 , 物理意义运动质点在映射 𝑓 下的对应点,在 𝑤0 的速度. • 比较两个速度的大小和方向,发现 𝑤 = 𝑓′ 𝑧0 ⋅ 𝑣 Ԧ ,Arg 𝑤 = Arg 𝑓′(𝑧0) + Arg𝑣 Ԧ 𝑓′ 𝑧0 为速度大小变化的比率,Arg 𝑓′(𝑧0) 为速度方向转动的角度.

映射共形性 若函数f(z)在区域D内解析且f'(zo)≠0,则过zo的任何一条 简单参数曲线在zo点的速度大小变化的比率都为|f'(zo)川,速度 方向转动的角度都为Argf'(zo),这样的映射称为在zo点共形! 保角性:共形映照保持过一点的两条曲线间的转动角不变!
映射共形性 • 若函数 𝑓(𝑧) 在区域 𝐷 内解析且 𝑓′ 𝑧0 ≠ 0,则过 𝑧0 的任何一条 简单参数曲线在 𝑧0 点的速度大小变化的比率都为 𝑓′ 𝑧0 ,速度 方向转动的角度都为 Arg 𝑓′(𝑧0),这样的映射称为在 𝑧0 点共形! • 保角性:共形映照保持过一点的两条曲线间的转动角不变!

02 PART 几种特殊的共形映照
几种特殊的共形映照 02 PART

指数函数与对数函数 指数函数e2在所有点都共形,对数函数lnz在所有解析点共形 将带形域映为角形域 D 指数函数局部存在反函数(对数函数)但不存在整体的反函数
指数函数与对数函数 指数函数 𝑒 𝑧 在所有点都共形,对数函数 ln 𝑧 在所有解析点共形. • 将带形域映为角形域 • 指数函数局部存在反函数(对数函数)但不存在整体的反函数
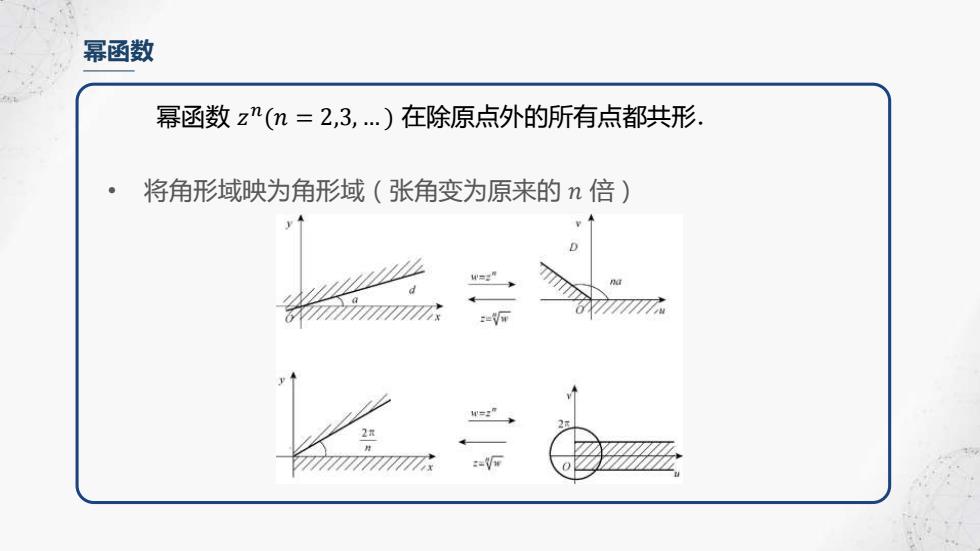
幂函数 幂函数zn(n=2,3,…)在除原点外的所有点都共形. 。 将角形域映为角形域(张角变为原来的n倍) 甲=2” 2
幂函数 幂函数 𝑧 𝑛 (𝑛 = 2,3, … ) 在除原点外的所有点都共形. • 将角形域映为角形域(张角变为原来的 𝑛 倍)