
01 Fourier变换 目录》 02 Fourier变换的运算性质 CONTENTS 03 Fourier:逆变换
01 Fourier 变换 目 录 CONTENTS 02 Fourier 变换的运算性质 03 Fourier 逆变换

01 PART Fourier变换
Fourier 变换 01 PART

Fourier变换 定义对定义在(-∞,+∞)上的函数f(x),称关于实变量ω的函数 十00 fo)=∫fe)e-lwdx -00 为f(x)的Fourier变换,e-iwx称为Fourier变换的核
Fourier 变换 定义 对定义在 −∞, +∞ 上的函数 𝑓(𝑥),称关于实变量 𝜔 的函数 𝑓መ 𝜔 = න −∞ +∞ 𝑓(𝑥)𝑒 −𝑖𝜔𝑥d𝑥 为 𝑓(𝑥) 的 Fourier 变换,𝑒 −𝑖𝜔𝑥 称为 Fourier 变换的核 .

注解 注1 Fourier变换将函数f(x)变换为f(w),因此Fourier变换可看作 函数到函数的映射.从映射的观点,称f(ω)为f(x)的像函数,f(x) 为f(ω)的原像函数. 注2并非对所有f(x),都可以定义f(ω)(定义式中的广义积分有可能 不收敛).若f(x)满足绝对可积条件,即1f(x)dx收敛,则f(ω) 对一切实变量ω有定义
注解 注1 Fourier 变换将函数 𝑓(𝑥) 变换为 𝑓መ 𝜔 ,因此 Fourier 变换可看作 函数到函数的映射.从映射的观点,称 𝑓መ 𝜔 为 𝑓(𝑥) 的像函数,𝑓 𝑥 为 𝑓መ 𝜔 的原像函数. 注2 并非对所有 𝑓(𝑥) ,都可以定义 𝑓መ 𝜔 (定义式中的广义积分有可能 不收敛).若 𝑓(𝑥) 满足绝对可积条件,即 ∞− +∞ 𝑓(𝑥) d𝑥 收敛,则 𝑓መ 𝜔 对一切实变量 𝜔 有定义.
例题 例1求f(x)=e-lw的Fourier变换. 解根据定义, +0∞ fω)= -00 e(1-i@)xx=0 e-(1+i@)xx=+oo 1 2 1-iw 1+iw 1X三-00
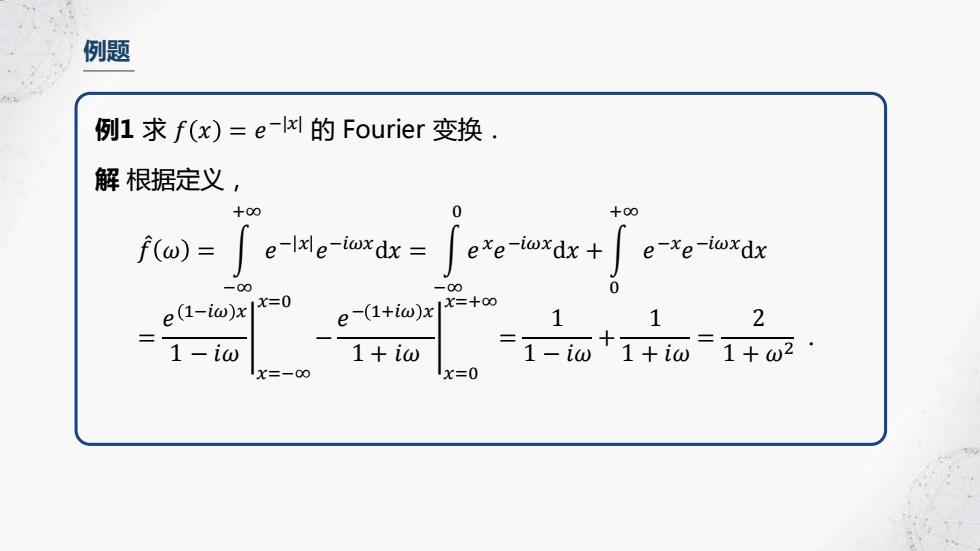
例题 例1 求 𝑓 𝑥 = 𝑒 −|𝑥| 的 Fourier 变换. 解 根据定义, 𝑓መ 𝜔 = න −∞ +∞ 𝑒 − 𝑥 𝑒 −𝑖𝜔𝑥d𝑥 = න −∞ 0 𝑒 𝑥 𝑒 −𝑖𝜔𝑥d𝑥 + න 0 +∞ 𝑒 −𝑥 𝑒 −𝑖𝜔𝑥d𝑥 = อ 𝑒 1−𝑖𝜔 𝑥 1 − 𝑖𝜔 𝑥=−∞ 𝑥=0 − อ 𝑒 − 1+𝑖𝜔 𝑥 1 + 𝑖𝜔 𝑥=0 𝑥=+∞ = 1 1 − 𝑖𝜔 + 1 1 + 𝑖𝜔 = 2 1 + 𝜔2 .

例题 求a-0图引 的Fourier变换. 解根据定义, 当ω≠0时, (ω)s- eiωxlX=1 2sinω ω 特别,(0)=2. 注可以证明,当f(x)绝对可积时,f(ω)一致连续且1imf(w)=0
例题 例2 求 𝑢 𝑥 = ቊ 1 𝑥 ≤ 1 0 𝑥 > 1 的 Fourier 变换. 解 根据定义, 𝑢ො 𝜔 = න −1 1 𝑒 −𝑖𝜔𝑥d𝑥 . 当 𝜔 ≠ 0 时, 𝑢ො 𝜔 = − อ 𝑒 −𝑖𝜔𝑥 𝑖𝜔 𝑥=−1 𝑥=1 = 2 sin 𝜔 𝜔 ; 特别,𝑢ො 0 = 2. 注 可以证明,当 𝑓(𝑥) 绝对可积时,𝑓መ 𝜔 一致连续且 lim 𝜔→∞ 𝑓መ 𝜔 = 0.

例题 例3求f)=的Fourier变换. 解根据定义, +00 -00 当w0时,f(o)=f(-ω)=πe-w.综合两种情形,f(o)=πewl
例题 例3 求 𝑓 𝑥 = 1 1+𝑥2 的 Fourier 变换. 解 根据定义, 𝑓መ 𝜔 = න −∞ +∞ 𝑒 −𝑖𝜔𝑥 1 + 𝑥 2 d𝑥 . 当 𝜔 0 时,𝑓መ 𝜔 = 𝑓(−𝜔) = 𝜋𝑒 −𝜔.综合两种情形,𝑓መ 𝜔 = 𝜋𝑒 −|𝜔|.

例题 例4求f(x)=e-2的Fourier变换 解根据定义, +00 十00 fa)=∫dx=∫cos dx -00 -00 根据Euler--Poisson积盼,得fw)=Vme号
例题 例4 求 𝑓 𝑥 = 𝑒 −𝑥 2 的 Fourier 变换. 解 根据定义, 𝑓መ 𝜔 = න −∞ +∞ 𝑒 −𝑥 2 𝑒 −𝑖𝜔𝑥d𝑥 = න −∞ +∞ 𝑒 −𝑥 2 cos 𝜔𝑥 d𝑥 . 根据 Euler-Poisson 积分,得 𝑓መ 𝜔 = 𝜋𝑒 − 𝜔2 4 .

02 PART Fourier变换的运算性质
Fourier 变换的运算性质 02 PART

运算性质 线性性质[l1f(x)+l2f2(x)]r=l1(ω)+l2(ω),其中l1,l2∈R. 位移性质f(x-a)r=e-iaf(ω),[eixaf(x)小=f(ω-a),其中a∈ R. 相似性质(kx=f(保),其中k为非零实数 卷积性质若,都绝对可积,则卷积 +00 后*)=ix-f0)y, 也绝对可积,且(丘*f2(x)少=(ω)f(ω). 导数性质若f和f'都绝对可积,则[f'(x)=iωf(ω)·
运算性质 线性性质 𝑙1𝑓1 𝑥 + 𝑙2𝑓2 𝑥 ̂= 𝑙1𝑓 1(𝜔) + 𝑙2𝑓 2(𝜔),其中 𝑙1, 𝑙2 ∈ 𝐑. 位移性质 𝑓 𝑥 − 𝑎 ̂= 𝑒 −𝑖𝜔𝑎𝑓መ(𝜔), 𝑒 𝑖𝑥𝑎𝑓 𝑥 ̂= 𝑓መ(𝜔 − 𝑎),其中 𝑎 ∈ 𝐑. 相似性质 𝑓 𝑘𝑥 ̂= 1 𝑘 𝑓መ 𝜔 𝑘 ,其中 𝑘 为非零实数. 卷积性质 若 𝑓1,𝑓2 都绝对可积,则卷积 𝑓1 ∗ 𝑓2 𝑥 = න −∞ +∞ 𝑓1 𝑥 − 𝑦 𝑓2 𝑦 d𝑦 , 也绝对可积,且 𝑓1 ∗ 𝑓2 𝑥 ̂= 𝑓 1(𝜔)𝑓 2(𝜔). 导数性质 若 𝑓 和 𝑓′ 都绝对可积,则 𝑓 ′ 𝑥 ̂= 𝑖𝜔𝑓መ(𝜔).