
目录》 01 复平面上的曲线 CONTENTS 02 复平面上的区域
目 录 01 复平面上的曲线 CONTENTS 02 复平面上的区域

01 PART 复平面上的曲线
复平面上的曲线 01 PART

参数方程与曲线的方向 定义若平面点集可以表示为由区间【α,b]到复平面的连续映射下的像集 则该点集就称为一条平面曲线,该映射称为该曲线的一个参数方程.按 照参数的增大或减小的方向可给出曲线的方向,参数增大的方向为曲线 的正方向(默认),参数减小的方向为曲线的反方向. 例1自点z1到点z2的有向线段z(t)=z1+t(z2-21),t∈[0,1]· 21
参数方程与曲线的方向 定义 若平面点集可以表示为由区间 𝑎, 𝑏 到复平面的连续映射下的像集, 则该点集就称为一条平面曲线,该映射称为该曲线的一个参数方程.按 照参数的增大或减小的方向可给出曲线的方向,参数增大的方向为曲线 的正方向(默认),参数减小的方向为曲线的反方向. 例1 自点 𝑧1 到点 𝑧2 的有向线段 𝑧 𝑡 = 𝑧1 + 𝑡 𝑧2 − 𝑧1 ,𝑡 ∈ 0,1 .

参数方程的不唯一性 注同一条平面曲线的参数方程表示不唯一 例2z(0)=z0+rei0,0∈[0,2m]和z(0)=z0+rei0,0∈[0,4π]都表 示以点zo为圆心,r为半径的圆周. 人
参数方程的不唯一性 注 同一条平面曲线的参数方程表示不唯一. 例2 𝑧 𝜃 = 𝑧0 + 𝑟𝑒 𝑖𝜃 ,𝜃 ∈ 0,2𝜋 和 𝑧 𝜃 = 𝑧0 + 𝑟𝑒 𝑖𝜃 ,𝜃 ∈ 0,4𝜋 都表 示以点 𝑧0 为圆心,𝑟 为半径的圆周.

曲线的切向量 定义若平面曲线可以表示为可导的参数方程(其导数称为该曲线的切向 量),则该曲线称为光滑曲线.若平面曲线可以表示为除了有限个点以 外处处可导的参数方程,则该曲线称为逐段光滑曲线· 注本课程中研究的曲线,都是逐段光滑的 例3求有向线段z(t)=z1+t(z2-z1),t∈[0,1]的切向量. 解先将方程写为实形式 x(t)=x1+t(x2-x1) 求导数 x'(t)=x2-x1 y(t)=y1+t0y2-y1) y(t)=y2-y1 将导数写回复形式z(t)=z2-21·
曲线的切向量 定义 若平面曲线可以表示为可导的参数方程(其导数称为该曲线的切向 量),则该曲线称为光滑曲线.若平面曲线可以表示为除了有限个点以 外处处可导的参数方程,则该曲线称为逐段光滑曲线. 注 本课程中研究的曲线,都是逐段光滑的. 例3 求有向线段 𝑧 𝑡 = 𝑧1 + 𝑡 𝑧2 − 𝑧1 ,𝑡 ∈ 0,1 的切向量. 解 先将方程写为实形式 ൝ 𝑥 𝑡 = 𝑥1 + 𝑡(𝑥2 − 𝑥1) 𝑦 𝑡 = 𝑦1 + 𝑡(𝑦2 − 𝑦1) 求导数 ቊ 𝑥′ 𝑡 = 𝑥2 − 𝑥1 𝑦′ 𝑡 = 𝑦2 − 𝑦1 将导数写回复形式 𝑧′ 𝑡 = 𝑧2 − 𝑧1 .

曲线的切向量 例4自z0经z1到z2折线段的参数方程 z(e)=o+t2-zo),0≤t≤1 z1+t(z2-z1),1≤t≤2 该曲线在t=1处通常不可导,故不是光滑曲线,但是逐段光滑的. 例5求圆周z(0)=z0+rei8,0e[0,2m]的切向量. 解先将方程写为实形式 x(0)=x0+rc0s0 求导数 (x'(0)=-rsine y(0)=yo +rsine Iy'(e)=rcose 将导数写回复形式z'(t)=-r(sin0-icos0)=irei8
曲线的切向量 例4 自 𝑧0 经 𝑧1 到 𝑧2 折线段的参数方程 𝑧 𝑡 = ൜ 𝑧0 + 𝑡 𝑧1 − 𝑧0 ,0 ≤ 𝑡 ≤ 1 𝑧1 + 𝑡(𝑧2 − 𝑧1),1 ≤ 𝑡 ≤ 2 该曲线在 𝑡 = 1 处通常不可导,故不是光滑曲线,但是逐段光滑的. 例5 求圆周 𝑧 𝜃 = 𝑧0 + 𝑟𝑒 𝑖𝜃 ,𝜃 ∈ 0,2𝜋 的切向量. 解 先将方程写为实形式 ൝ 𝑥 𝜃 = 𝑥0 + 𝑟 cos 𝜃 𝑦 𝜃 = 𝑦0 + 𝑟 sin 𝜃 求导数 ቊ 𝑥 ′ 𝜃 = −𝑟 sin 𝜃 𝑦′ 𝜃 = 𝑟 cos𝜃 将导数写回复形式 𝑧 ′ 𝑡 = −𝑟 sin 𝜃 − 𝑖 cos𝜃 = 𝑖𝑟𝑒 𝑖𝜃 .
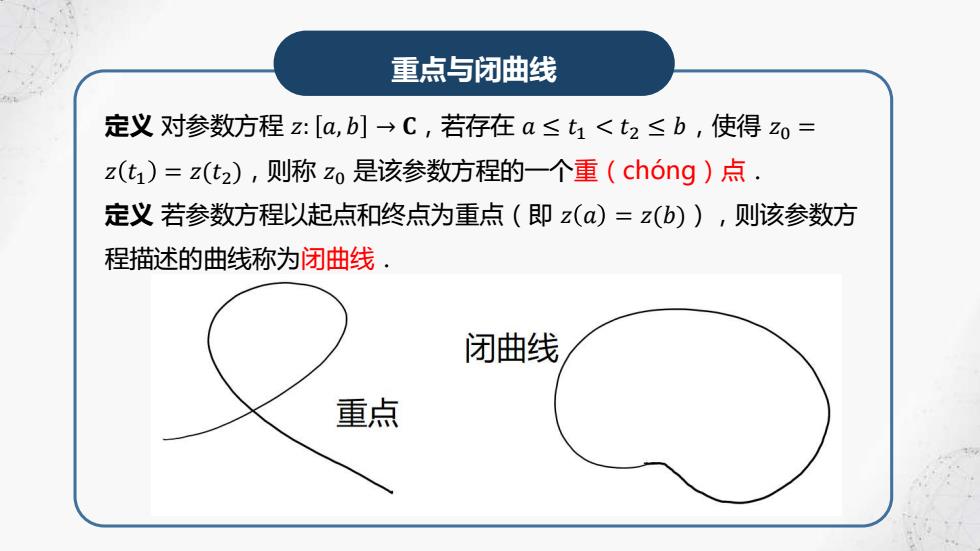
重点与闭曲线 定义对参数方程z:[a,b]→C,若存在a≤t1<t2≤b,使得z0= z(t1)=z(t2),则称z0是该参数方程的一个重(ch6ng)点. 定义若参数方程以起点和终点为重点(即z(a)=z(b)),则该参数方 程描述的曲线称为闭曲线, 闭曲线 重点
重点与闭曲线 定义 对参数方程 𝑧: 𝑎, 𝑏 → 𝐂,若存在 𝑎 ≤ 𝑡1 < 𝑡2 ≤ 𝑏,使得 𝑧0 = 𝑧 𝑡1 = 𝑧(𝑡2),则称 𝑧0 是该参数方程的一个重(chóng)点. 定义 若参数方程以起点和终点为重点(即 𝑧 𝑎 = 𝑧(𝑏)),则该参数方 程描述的曲线称为闭曲线.
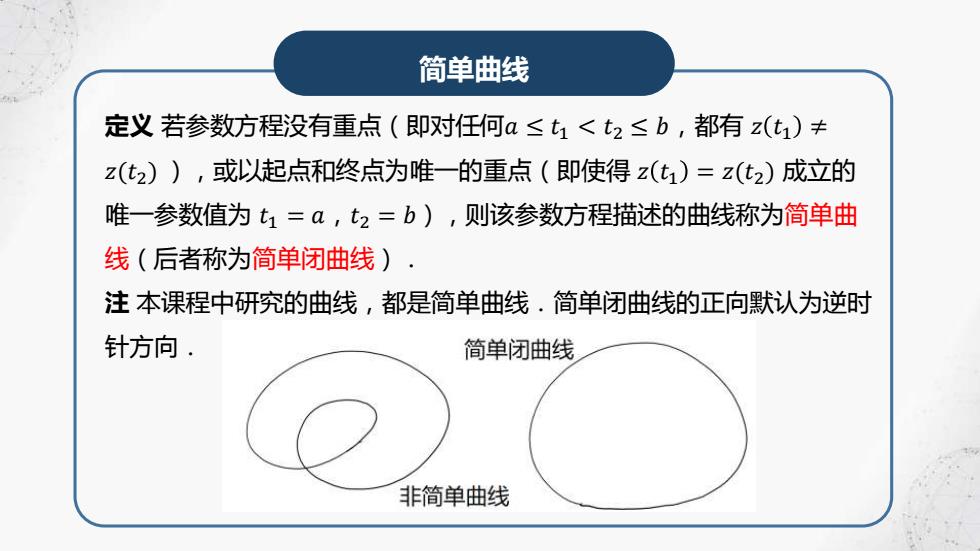
简单曲线 定义若参数方程没有重点(即对任何a≤t1<t2≤b,都有z(t1)≠ z(t2)),或以起点和终点为唯一的重点(即使得z(t1)=z(t2)成立的 唯一参数值为t1=Q,t2=b),则该参数方程描述的曲线称为简单曲 线(后者称为简单闭曲线). 注本课程中研究的曲线,都是简单曲线.简单闭曲线的正向默认为逆时 针方向. 简单闭曲线 非简单曲线
简单曲线 定义 若参数方程没有重点(即对任何𝑎 ≤ 𝑡1 < 𝑡2 ≤ 𝑏,都有 𝑧 𝑡1 ≠ 𝑧(𝑡2) ),或以起点和终点为唯一的重点(即使得 𝑧 𝑡1 = 𝑧(𝑡2) 成立的 唯一参数值为 𝑡1 = 𝑎,𝑡2 = 𝑏),则该参数方程描述的曲线称为简单曲 线(后者称为简单闭曲线). 注 本课程中研究的曲线,都是简单曲线.简单闭曲线的正向默认为逆时 针方向.

02 PART 复平面上的区域
复平面上的区域 02 PART

内点与开集 定义集合{z:lz-w川<e}称为点w的e-邻域,记作Be(w)· 定义对平面点集S中的一点z,若存在z的e-邻域B(z)cS,则称 z是S的内点.若S中的所有点都是S的内点,则称S是平面上的开 集.特别,规定空集为开集
内点与开集 定义 集合 {𝑧: 𝑧 − 𝑤 < 𝜀} 称为点 𝑤 的 𝜖 −邻域,记作 𝐵𝜀 (𝑤) . 定义 对平面点集 𝑆 中的一点 𝑧,若存在 𝑧 的 𝜖 −邻域 𝐵𝜀 𝑧 ⊂ 𝑆,则称 𝑧 是 𝑆 的内点.若 𝑆 中的所有点都是 𝑆 的内点,则称 𝑆 是平面上的开 集.特别,规定空集为开集.