
Direct Method for the Solution of Linear Equations →Introduction Naive Gaussian Elimination .Limitations and Operation Counts ●LU factorization ●QR factorization Copyright©2011,NA⊙Yin Last Modification:Oct.2011 2
Direct Method for the Solution of Linear Equations ⇒ Introduction • Naive Gaussian Elimination • Limitations and Operation Counts • LU factorization • QR factorization Copyright c 2011, NA Yin Last Modification: Oct. 2011 2

What Are Linear Equations (LEs)? a11x1+ a12x2 三 b1 a21x1+a22x2+. 62 + 十··· 十 三 am11+am2x2+·+AmnEn =bm ●Dependence on unknowns:powers of degree≤I 。Summation form::∑1ajgj=bi,1≤i≤m,i.e,m equations Presently:m =n,i.e.,square systems (later:m n) Q:How to solve for [1 22...n]T?A:... Copyright©2011,NA⊙Yin Last Modification:Oct.2011 3
What Are Linear Equations (LEs)? a11x1 + a12x2 + · · · + a1nxn = b1 a21x1 + a22x2 + · · · + a2nxn = b2 ... + ... + · · · + ... = ... am1x1 + am2x2 + · · · + amnxn = bm • Dependence on unknowns: powers of degree ≤ 1 • Summation form: Pn j=1 aijxj = bi , 1 ≤ i ≤ m, i.e., m equations • Presently: m = n, i.e., square systems (later: m 6= n) Q: How to solve for x1 x2 . . . xn T ? A: . . . Copyright c 2011, NA Yin Last Modification: Oct. 2011 3��

Gaussian Elimination ●Introduction Naive Gaussian Elimination .Limitations and Operation Counts ●LU factorization ●QR factorization Copyright©2011,NA⊙Yin Last Modification:Oct.2011 4
Gaussian Elimination • Introduction ⇒ Naive Gaussian Elimination • Limitations and Operation Counts • LU factorization • QR factorization Copyright c 2011, NA Yin Last Modification: Oct. 2011 4

Overall Algorithm and Definitions Currently:direct method only (later:iterative methods) ●General idea: Generate upper triangular system("forward elimination") Easily calculate unknowns in reverse order ("backward substitution") ."Pivot row"=current one being processed "pivot"=diagonal element of pivot row Steps applied to RHS as well.(RHS:Right hand side vector. Copyright©2011,NA⊙Yin Last Modification:Oct.2011 5
Overall Algorithm and Definitions • Currently: direct method only (later: iterative methods) • General idea: ∗ Generate upper triangular system (”forward elimination”) ∗ Easily calculate unknowns in reverse order (”backward substitution”) • ”Pivot row” = current one being processed ”pivot” = diagonal element of pivot row • Steps applied to RHS as well. (RHS: Right hand side vector.) Copyright c 2011, NA Yin Last Modification: Oct. 2011 5

Forward Elimination Generate zero columns below diagonal Process rows downward for each row i:=1,n-1 /the pivot row for each row k:=i+1,n V rows below pivot multiply pivot row aii=aki subtract pivot row from row k /now aki=0 }/now column below ai is zero now /aij=0,vi>j Obtain triangular system Let's work an example,.. Copyright 2011,NAOYin Last Modification:Oct.2011 6
Forward Elimination • Generate zero columns below diagonal • Process rows downward for each row i := 1, n − 1 { // the pivot row for each row k := i + 1, n { ∀ rows below pivot multiply pivot row aii = aki subtract pivot row from row k // now aki = 0 } // now column below aii is zero } now // aij = 0, ∀ i > j • Obtain triangular system Let’s work an example, ... Copyright c 2011, NA Yin Last Modification: Oct. 2011 6
Matrix Form of Linear Equations 6x1 2x2 2x3 + 4x4 = 16 12x1 8x2 6x3 10x4 = 26 3x1 13c2 十 9x3 + 3x4 -19 6x1 + 4c2 + 1x3 18x4 = -34 Matrix form 6 -2 2 ¥ X1 16 12 -8 6 10 T2 26 b 3 -13 9 3 T3 -19 -6 4 1 -18 -34 Copyright©2011,NA⊙Yin Last Modification:Oct.2011 7
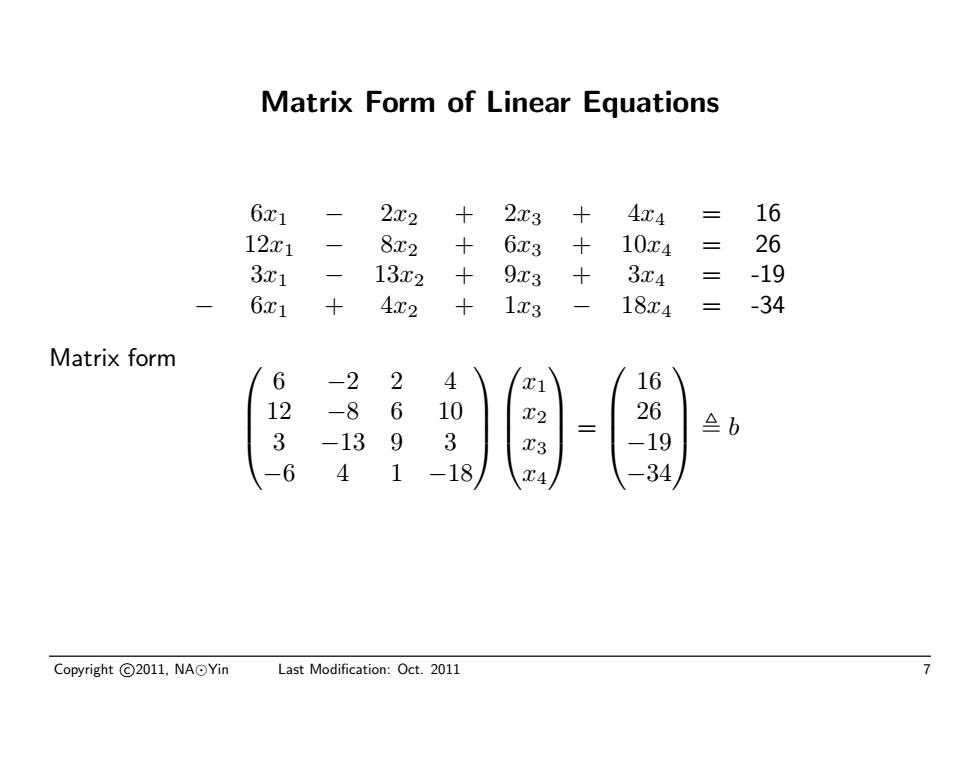
Matrix Form of Linear Equations 6x1 − 2x2 + 2x3 + 4x4 = 16 12x1 − 8x2 + 6x3 + 10x4 = 26 3x1 − 13x2 + 9x3 + 3x4 = -19 − 6x1 + 4x2 + 1x3 − 18x4 = -34 Matrix form 6 −2 2 4 12 −8 6 10 3 −13 9 3 −6 4 1 −18 x1 x2 x3 x4 = 16 26 −19 −34 , b Copyright c 2011, NA Yin Last Modification: Oct. 2011 7

Compact Form of Linear Equations 6x1 2x2 2x3 4x4 = 16 12x1 8x2 6x3 10x4 26 3x1 13x2 9x3 3x4 -19 6x1 + 4x2 +1x3 一 18x4 = -34 Compact form 6 -2 2 4 16 12 -8 6 10 26 3 -139 3 -19 -6 4 1 -18 -34 Proceeding with the forward elimination,.. Copyright©2011,NA⊙Yin Last Modification:Oct.2011 8
Compact Form of Linear Equations 6x1 − 2x2 + 2x3 + 4x4 = 16 12x1 − 8x2 + 6x3 + 10x4 = 26 3x1 − 13x2 + 9x3 + 3x4 = -19 − 6x1 + 4x2 + 1x3 − 18x4 = -34 Compact form 6 −2 2 4 16 12 −8 6 10 26 3 −13 9 3 −19 −6 4 1 −18 −34 Proceeding with the forward elimination, ... Copyright c 2011, NA Yin Last Modification: Oct. 2011 8

Forward Elimination-Example 6 -2 2 4 16 6 -2 4 16 -8 6 10 26 0 -4 2 -6 3 -13 9 3 -19 → 0 -12 1 -27 6 4 -18 -34 0 2 3 -14 -18 6 -2 2 4 16 6 -22 4 16 0 -4 2 2 -6 0 -4 2 2 6 → 0 0 2 -5 9 0 0 2 5 0 0 -13 -21 0 0 0 3 Matrix is upper triangular. Copyright©2011,NA⊙Yin Last Modification:Oct.2011 9
Forward Elimination–Example 6 −2 2 4 16 12 −8 6 10 26 3 −13 9 3 −19 −6 4 1 −18 −34 → 6 −2 2 4 16 0 −4 2 2 −6 0 −12 8 1 −27 0 2 3 −14 −18 → 6 −2 2 4 16 0 −4 2 2 −6 0 0 2 −5 −9 0 0 4 −13 −21 → 6 −2 2 4 16 0 −4 2 2 −6 0 0 2 −5 −9 0 0 0 −3 −3 Matrix is upper triangular. Copyright c 2011, NA Yin Last Modification: Oct. 2011 9

Upper Sum 6 -2 2 4 16 0 -4 2 2 -6 0 0 2 -5 -9 0 0 0 -3 -3 ●Last equation:-3x4=-3→x4=1 .Second to last equation:23-5 4 =23-5=-9 3=-2 =1 ..second equation...2=... ·12x3x4=B1-21]T 7 For small problems,check solution in original system. Copyright©2011,NA⊙Yin Last Modification:Oct.2011 10
Upper Sum 6 −2 2 4 16 0 −4 2 2 −6 0 0 2 −5 −9 0 0 0 −3 −3 • Last equation: −3x4 = −3 ⇒ x4 = 1 • Second to last equation: 2x3 − 5 x4 |{z} =1 = 2x3 − 5 = −9 ⇒ x3 = −2 • . . . second equation . . . x2 = . . . • x1 x2 x3 x4 T = 3 1 −2 1T For small problems, check solution in original system. Copyright c 2011, NA Yin Last Modification: Oct. 2011 10����

Linear Systems ●Introduction Naive Gaussian Elimination Limitations and Operation Counts ●LU factorization ●QR factorization Copyright©2011,NA⊙Yin Last Modification:Oct.2011 11
Linear Systems • Introduction • Naive Gaussian Elimination ⇒ Limitations and Operation Counts • LU factorization • QR factorization Copyright c 2011, NA Yin Last Modification: Oct. 2011 11