
01 三角形式和指数形式 目录》 02 幂与根 CONTENTS 03 球极投影
01 三角形式和指数形式 目 录 CONTENTS 02 幂与根 03 球极投影

01 PART 三角形式与指数形式
三角形式与指数形式 01 PART
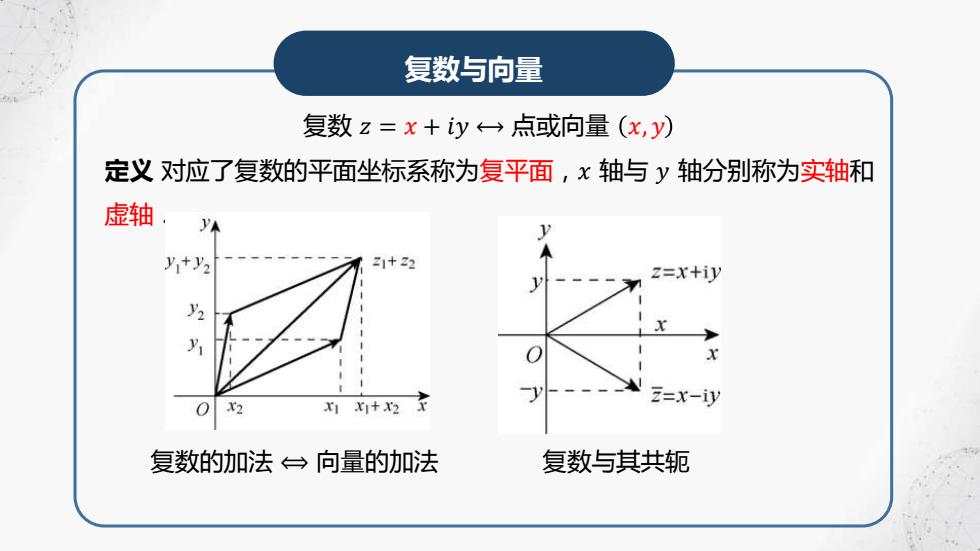
复数与向量 复数z=x+iy←→点或向量(x,y) 定义对应了复数的平面坐标系称为复平面,x轴与y轴分别称为实轴和 虚轴 1 +y2 21+22 z=x+iy X2 X1X+X2 z=x-iy 复数的加法台向量的加法 复数与其共轭
复数与向量 复数 𝑧 = 𝑥 + 𝑖𝑦 ⟷ 点或向量 𝑥, 𝑦 定义 对应了复数的平面坐标系称为复平面,𝑥 轴与 𝑦 轴分别称为实轴和 虚轴. 复数的加法 ⟺ 向量的加法 复数与其共轭
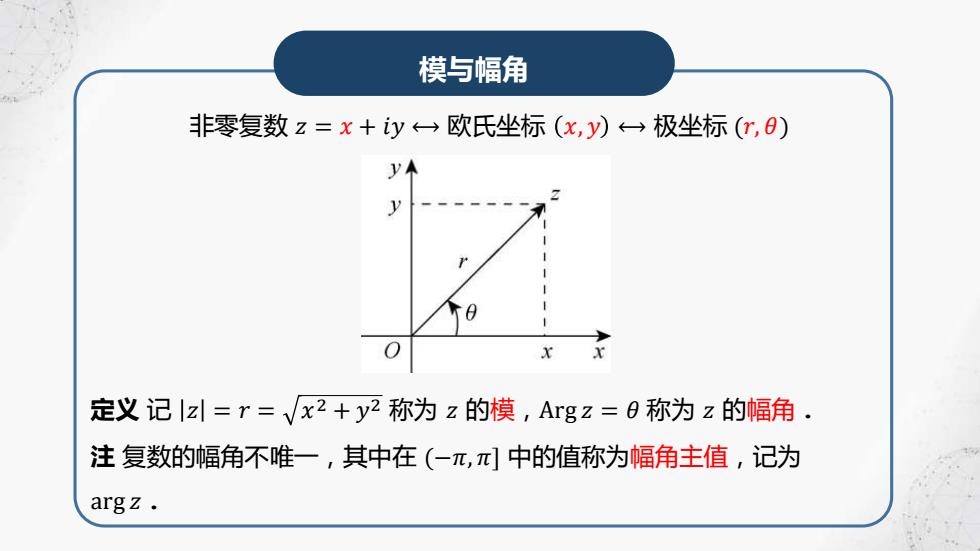
模与幅角 非零复数z=x+y←→欧氏坐标(x,y)←→极坐标(亿,) y 定义记|z=r=√x2+y2称为z的模,Argz=0称为z的幅角. 注复数的幅角不唯一,其中在(-兀,π]中的值称为幅角主值,记为 argz
模与幅角 非零复数 𝑧 = 𝑥 + 𝑖𝑦 ⟷ 欧氏坐标 𝑥, 𝑦 ⟷ 极坐标 (𝑟, 𝜃) 定义 记 𝑧 = 𝑟 = 𝑥 2 + 𝑦 2 称为 𝑧 的模,Arg 𝑧 = 𝜃 称为 𝑧 的幅角. 注 复数的幅角不唯一,其中在 (−𝜋, 𝜋] 中的值称为幅角主值,记为 arg 𝑧.

三角形式 定义对复数z,若其在复平面对应点的极坐标为(工,),则称表达式 z=r(cos0+isin0) 为该复数的三角形式· 定理若z1=h(cos01+isin01),z2=2(cos02+isin日2),则 z1z2=12(cos(01+02)+isin(01+02). 证明只需注意到 (cos01+isin01)(cos02 +isin02) =(cos01 cos02-sin 01 sin 02)+i(sin 01 cos02 +cos01 sin02) =cos(01+02)+isin(01+02) 即可
三角形式 定义 对复数 𝑧,若其在复平面对应点的极坐标为 𝑟, 𝜃 ,则称表达式 𝑧 = 𝑟(cos 𝜃 + 𝑖 sin 𝜃) 为该复数的三角形式. 定理 若 𝑧1 = 𝑟1(cos𝜃1 + 𝑖 sin 𝜃1),𝑧2 = 𝑟2(cos𝜃2 + 𝑖 sin 𝜃2),则 𝑧1𝑧2 = 𝑟1𝑟2(cos(𝜃1 + 𝜃2) + 𝑖 sin(𝜃1 + 𝜃2)). 证明 只需注意到 cos 𝜃1 + 𝑖 sin 𝜃1 cos𝜃2 + 𝑖 sin 𝜃2 = (cos𝜃1 cos𝜃2 − sin 𝜃1 sin 𝜃2) + 𝑖 (sin 𝜃1 cos𝜃2 + cos𝜃1 sin 𝜃2) = cos(𝜃1 + 𝜃2) + 𝑖 sin(𝜃1 + 𝜃2) 即可.

模与幅角的运算性质 定理(1)max{Rez引,lmz}≤|z; (2)|z1±z2l≤lz1l+lz2l; (3)1zz21=Izallz21; (4)z1z2的幅角等于z1与z2各自幅角的和,但arg(z1z2)=argz1+ argz2一般不成立; (5)lz-11=lz-1; (6)|=z,zz=|z2
模与幅角的运算性质 定理 (1) max Re 𝑧 , Im 𝑧 ≤ 𝑧 ; (2) 𝑧1 ± 𝑧2 ≤ |z1| + |𝑧2|; (3) 𝑧1𝑧2 = |z1||𝑧2|; (4) 𝑧1𝑧2 的幅角等于 𝑧1 与 𝑧2 各自幅角的和,但 arg(𝑧1𝑧2) = arg 𝑧1 + arg 𝑧2 一般不成立; (5) |𝑧 −1 | = 𝑧 −1; (6) 𝑧ҧ = |𝑧|,𝑧𝑧ҧ= 𝑧 2 .

指数形式 定义记ei0=cos0+isin0,称为复数的指数形式. 注l指数形式的记法由Euer首先提出,也称为Euler公式,该公式可 通过指数函数的Taylor公式形式地得到 +-品 ●● 00 00 cos0 +isin= n=0 n=0 n=0 =eig 注2通过Euler公式,三角形式下的乘积公式可写为 Z122=(1ei8)(2ei0)=n2ei61+8,), 即实指数运算的性质对纯虚指数也成立. 注3因e|=1,故e0也称为单位复数
指数形式 定义 记 𝑒 𝑖𝜃 = cos𝜃 + 𝑖 sin 𝜃,称为复数的指数形式. 注1 指数形式的记法由 Euler 首先提出,也称为 Euler 公式,该公式可 通过指数函数的 Taylor 公式形式地得到 cos𝜃 + 𝑖 sin 𝜃 = 𝑛=0 ∞ −1 𝑛 2𝑛 ! 𝜃 2𝑛 + 𝑖 𝑛=0 ∞ −1 𝑛 2𝑛 + 1 ! 𝜃 2𝑛+1 = 𝑛=0 ∞ 𝑖 𝑛 𝑛! 𝜃 𝑛 = 𝑒 𝑖𝜃. 注2 通过 Euler 公式,三角形式下的乘积公式可写为 𝑧1𝑧2 = (𝑟1𝑒 𝑖𝜃1)(𝑟2𝑒 𝑖𝜃2) = 𝑟1𝑟2𝑒 𝑖 𝜃1+𝜃2 , 即实指数运算的性质对纯虚指数也成立. 注3 因 𝑒 𝑖𝜃 = 1,故 𝑒 𝑖𝜃 也称为单位复数.

02 PART 幂与根
幂与根 02 PART

整数次幂 定义规定z0=1,当n为正整数时,z=z·zn-1,zm=(z)1. 定理对z=rei,n为整数,有zn=rnein9. 例计算(-1+)3. 解法一根据二项式定理 (-1+i)3=-1+3i-3i2+i3=2+2i. 解法二|-1+i=V2,arctan(-1)=-牙,而-1+i在第二象限,从 而arg(-1+0-买,即-1+i=2e受.于是 (←1+0=w2e停-22受+号 =2+2i
整数次幂 定义 规定 𝑧 0 = 1,当 𝑛 为正整数时,𝑧 𝑛 = 𝑧 ⋅ 𝑧 𝑛−1 ,𝑧 −𝑛 = 𝑧 𝑛 −1. 定理 对 𝑧 = 𝑟𝑒 𝑖𝜃 , 𝑛 为整数,有 𝑧 𝑛 = 𝑟 𝑛 𝑒 𝑖𝑛𝜃. 例 计算 −1 + 𝑖 3. 解法一 根据二项式定理 −1 + 𝑖 3 = −1 + 3𝑖 − 3𝑖 2 + 𝑖 3 = 2 + 2𝑖. 解法二 −1 + 𝑖 = 2,arctan(−1) = − 𝜋 4 ,而 −1 + 𝑖 在第二象限,从 而 arg(−1 + 𝑖) = 3π 4 ,即 −1 + 𝑖 = 2𝑒 𝑖 3𝜋 4 .于是 −1 + 𝑖 3 = 2 3 𝑒 𝑖 9𝜋 4 = 2 2 2 2 + 𝑖 2 2 = 2 + 2𝑖.

正整数次根 对非零复数z=rei以及正整数n,考虑方程wn=z.为此设 w=pei0,则 r=pn,np=0+2kπ(k∈Z), 从而w=Ve2.当k=0,1“,n-1时,相应的0值之差小于2m 故相应的w值互不相同.而k与k+n相应的p值恰为2π,相应的w 值相同. De Moivre定理对任意非零复数z=rei诏以及正整数n,恰有n个不 同的n次方根,记为 z品=Vet .8+2kπ (k=0,1,…,n-1)
正整数次根 对非零复数 𝑧 = 𝑟𝑒 𝑖𝜃 以及正整数 𝑛,考虑方程 𝑤 𝑛 = 𝑧.为此设 𝑤 = 𝜌𝑒 𝑖𝜑,则 𝑟 = 𝜌 𝑛 ,𝑛𝜑 = 𝜃 + 2𝑘𝜋 (𝑘 ∈ 𝐙), 从而 𝑤 = 𝑛 𝑟𝑒 𝑖 𝜃+2𝑘𝜋 𝑛 .当 𝑘 = 0,1, ⋯ , 𝑛 − 1 时,相应的 𝜑 值之差小于 2𝜋, 故相应的 𝑤 值互不相同.而 𝑘 与 𝑘 + 𝑛 相应的 𝜑 值恰为 2𝜋,相应的 𝑤 值相同. De Moivre 定理 对任意非零复数 𝑧 = 𝑟𝑒 𝑖𝜃 以及正整数 𝑛,恰有 𝑛 个不 同的 𝑛 次方根,记为 𝑧 1 𝑛 = 𝑛 𝑟𝑒 𝑖 𝜃+2𝑘𝜋 𝑛 (𝑘 = 0,1, ⋯, 𝑛 − 1).