
目录 第一章线性方程组 7 S1.1消元解法 。。。g。。。。8。。,。。。g。。g。。。,。。。。。。。g。。,。。。。。 S12矩阵表示 11 第二章矩阵运算 15 S2.1基本概念 15 82.2分块佰阵 24 s2.3初等方民 。。4。。。。4。。。。。。。。4。。4。。。4。。。4。。。。4。。44。。。。。 S2.4可逆矩阵 31 第三章行列试 37 S3.1行列式的定义, 37 s3.2 Binet..Cauchy公式 2 33 Laplace展开···49 $3.4行列式与几何 54 第四章矩阵的相抵 57 S4.1矩阵的秩与相抵 57 S1.2相抵标准形的应用 ”··。”。。。。。”·4。”。·。”·。”·。。。··”。。。。 第五章矩阵的相似 77 S5.1相似的概念 77 S5.2相似三角化 84 55.3 Jordan标准形 65.4最小多项式 。,。。 94 55.5特征方阵 98 第六章正交方阵 103 S6.1正交方阵 103 6.2正交相似 10g S6.3正交相抵 ··.112 S6,4酉方阵 .116
目录 第一章 线性方程组 7 §1.1 消元解法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 §1.2 矩阵表示 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 第二章 矩阵运算 15 §2.1 基本概念 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 §2.2 分块矩阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 §2.3 初等方阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 §2.4 可逆矩阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 第三章 行列式 37 §3.1 行列式的定义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 §3.2 Binet-Cauchy 公式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 §3.3 Laplace 展开 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49 §3.4 行列式与几何 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 第四章 矩阵的相抵 57 §4.1 矩阵的秩与相抵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 §4.2 相抵标准形的应用 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 §4.3 Smith 标准形 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 第五章 矩阵的相似 77 §5.1 相似的概念 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 §5.2 相似三角化 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 §5.3 Jordan 标准形 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89 §5.4 最小多项式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94 §5.5 特征方阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98 第六章 正交方阵 103 §6.1 正交方阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103 §6.2 正交相似 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 §6.3 正交相抵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112 §6.4 酉方阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116 5

目录 第七章二次型 121 S7.1二次型的化荷 121 S7.2正定方阵 126 S7.3一些例子 ……………130 第八章线性空间 133 S8.1基本概念 .133 S8.2线性相关 58.3向量组的秩 …………………137 到 S8.4基与坐标 88.5交空间与和空间 147 S8.6直和与补空间 ··。。··。。·。。。··。·4。。··。···。··。。·4 .1560 第九章线性变换 155 69.1基本概念 155 S9.2线性映射的运算 .159 S9.3对偶空间 。。。。。。。。。”””。。。,。。”,””。,”。。,。。。,””。。 .162 94核空间与像空间.。··.·····…···。········。······165 S9.5不变子空间., ·,168 9.6根子空间 9.7循环子空间 17 第十章内积空间 179 S10.1基本概念 。179 S102标准正交基.184 810.3正交变换 ,189 S10.4伴随变换 S105复内积空间.·。 197 S10.6内积的推广 201 附录A多项式 205 8A1一元名项式 205 写A2多元多项式…·… ,215 参考文献 223
6 目录 第七章 二次型 121 §7.1 二次型的化简 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121 §7.2 正定方阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 §7.3 一些例子 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130 第八章 线性空间 133 §8.1 基本概念 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133 §8.2 线性相关 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137 §8.3 向量组的秩 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141 §8.4 基与坐标 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 §8.5 交空间与和空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147 §8.6 直和与补空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150 §8.7 直积与商空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153 第九章 线性变换 155 §9.1 基本概念 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155 §9.2 线性映射的运算 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159 §9.3 对偶空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162 §9.4 核空间与像空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165 §9.5 不变子空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168 §9.6 根子空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170 §9.7 循环子空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174 第十章 内积空间 179 §10.1 基本概念 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179 §10.2 标准正交基 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184 §10.3 正交变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189 §10.4 伴随变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192 §10.5 复内积空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197 §10.6 内积的推广 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201 附录 A 多项式 205 §A.1 一元多项式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 §A.2 多元多项式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215 参考文献 223

第一章线性方程组 线性方程组是最简单也是最重要的一类代数方程组,在科学研究和生产实践等领域中都有着厂 泛的应用.线性方程组求解问题具有非常久远的历史,中国古代数学名著《九章算术》(成书于约公 元前150年)中就记载着线性方程组的消元解法.线性方程组求解问题的研究促进了线性空间、线 性变换以及矩阵理论的建立和发展,构成了线性代数这门数学分支学科的中心内容 本章主要介绍一般的刀元线性方程组 a1n1+a122+…+a1nn=b a211+a222+…+a2nxn=b2 (11) an1t1十am2E2+·十amn工n=bm 的求解方法,其中a11,a12,…,amm,b1,2…,bnm是已知的数,,2,…,n是待求解的变量.特 别,当 =0时,线性方程组(1.)称为齐次线性方程组。 关于线性方程组,有下列几个基本问题。在本章以及后续的章节中,将从不同的角度来研究这 些问题. 1.解的存在性问题.线性方程组(11)是否有解? 2.解的唯一性问题.线性方程组(1.1)是否有唯一解? 3.解集的结构问题.线性方程组(11)的解集有何性质? 在本书中,数指的是某个数域中的元素。数域F是一个定义了加、减、乘、除运算,并且满足 特定运算律的非空集合,详见定义8.2.若存在素数p使得工+…+芝=0,z∈F,则p称为四 的特征,记作Char F=p.香则,规定CharF=0.例如,无限域C,R,Q的特征为0,g元有限域 Fg的特征为p,其中q是素数p的方幂. s1.1消元解法 求解代数方程组的基本思想是“消元法”:由原方程不断产生新方程,并且不断减少每个新方 程所包含未知数的个数,直到求出一个未知数:然后如法炮制求出其它未知数。在求解过程中有可 能得到“增根”,因此还需要把所求得的“可能解”代入原方程组进行检验,这样才能得到方程组的 真正解。对于非线性方程组,很难做到不产生“增根”.然而对于线性方程组,可以进行如下的同解 变形,以避免“验根”所带来的额外运算
第一章 线性方程组 线性方程组是最简单也是最重要的一类代数方程组,在科学研究和生产实践等领域中都有着广 泛的应用.线性方程组求解问题具有非常久远的历史,中国古代数学名著《九章算术》(成书于约公 元前 150 年)中就记载着线性方程组的消元解法.线性方程组求解问题的研究促进了线性空间、线 性变换以及矩阵理论的建立和发展,构成了线性代数这门数学分支学科的中心内容. 本章主要介绍一般的 n 元线性方程组 a11x1 + a12x2 + · · · + a1nxn = b1 a21x1 + a22x2 + · · · + a2nxn = b2 · · · · · · · · · · · · am1x1 + am2x2 + · · · + amnxn = bm (1.1) 的求解方法,其中 a11, a12, · · · , amn, b1, b2 · · · , bm 是已知的数,x1, x2, · · · , xn 是待求解的变量.特 别,当 b1 = b2 = · · · = bm = 0 时,线性方程组 (1.1) 称为齐次线性方程组. 关于线性方程组,有下列几个基本问题.在本章以及后续的章节中,将从不同的角度来研究这 些问题. 1. 解的存在性问题.线性方程组 (1.1) 是否有解? 2. 解的唯一性问题.线性方程组 (1.1) 是否有唯一解? 3. 解集的结构问题.线性方程组 (1.1) 的解集有何性质? 在本书中,数指的是某个数域中的元素.数域 F 是一个定义了加、减、乘、除运算,并且满足 特定运算律的非空集合.详见定义 8.2.若存在素数 p 使得 x + · · · + x | {z } p 个 = 0,∀x ∈ F,则 p 称为 F 的特征,记作 Char F = p.否则,规定 Char F = 0.例如,无限域 C, R, Q 的特征为 0,q 元有限域 Fq 的特征为 p,其中 q 是素数 p 的方幂. §1.1 消元解法 求解代数方程组的基本思想是“消元法”:由原方程不断产生新方程,并且不断减少每个新方 程所包含未知数的个数,直到求出一个未知数;然后如法炮制求出其它未知数.在求解过程中有可 能得到“增根”,因此还需要把所求得的“可能解”代入原方程组进行检验,这样才能得到方程组的 真正解.对于非线性方程组,很难做到不产生“增根”.然而对于线性方程组,可以进行如下的同解 变形,以避免“验根”所带来的额外运算. 7

第一章钱性方程组 例1.1.求解线性方程组 2-=-1 x1-2x2=-4 3x1-2x2+x4=-7 ③ 3m1+2+x3+3x4=0回 解答.④-③,得 3r2+x+2m4=7 方程组0,②,③,⊙的解一定满足方程组0.②,③,⑤.反之,④=③+⑤,方程组0,@,③,⑥的解 定满足方程组0,@,③,Q.因此,方程组①,@,③,④与方程组①,@,③,⑥的解集相同. 同理,③-3×②,得同解方程组,②⑥,⑤,其中 4r2+r4=5 ⑥-3×①,得同解方程组0,@,©,⊙,其中 43+24=10 ©-4×①,得同解方程组0,②,⊙,⊙,其中 43+x4=9 ⊙-®,得同解方程组①,②,®,@,其中 E=1 把4代入⊙,得到3=2.把xa代入①,得到2=1.把2代入回,得到1=-2. ◇ 全思考:把已解出的未知数代入某个方程求得其它未知数的过程是否有可能产生“增根? 定理11.对于线性方程组的下列操作不改变线性方程组的解 1.交换某两个方程在线性方程组中的位置,其它方程不变 县.把某个方程替换成它的非零常数倍,其它方程不变。 3.把某个方程替换成它与另一方程的常数倍之和,其它方程不变. 其中方程a1十a22十…十ann=b的常数入倍定义为 (Aa)m+(a2)2+…+(Aan)zn=(b) 两个方程a11+22+…+anxn=b与a(x1+a2十…十anxn=b之和定义为 (a1+4)1+(a2+a)z2+…+(an+)zn=(b+) 定义1.1.以上三类操作,称为对于线性方程组的初等变换
8 第一章 线性方程组 例 1.1. 求解线性方程组 x2 − x3 = −1 ⃝1 x1 − 2x2 = −4 ⃝2 3x1 − 2x2 + x4 = −7 ⃝3 3x1 + x2 + x3 + 3x4 = 0 ⃝4 解答. ⃝4 − ⃝3 ,得 3x2 + x3 + 2x4 = 7 ⃝5 方程组⃝1 ,⃝2 ,⃝3 ,⃝4 的解一定满足方程组⃝1 ,⃝2 ,⃝3 ,⃝5 .反之,⃝4 = ⃝3 + ⃝5 ,方程组⃝1 ,⃝2 ,⃝3 ,⃝5 的解一 定满足方程组⃝1 ,⃝2 ,⃝3 ,⃝4 .因此,方程组⃝1 ,⃝2 ,⃝3 ,⃝4 与方程组⃝1 ,⃝2 ,⃝3 ,⃝5 的解集相同. 同理,⃝3 − 3 × ⃝2 ,得同解方程组⃝1 ,⃝2 ,⃝6 ,⃝5 ,其中 4x2 + x4 = 5 ⃝6 ⃝5 − 3 × ⃝1 ,得同解方程组⃝1 ,⃝2 ,⃝6 ,⃝7 ,其中 4x3 + 2x4 = 10 ⃝7 ⃝6 − 4 × ⃝1 ,得同解方程组⃝1 ,⃝2 ,⃝8 ,⃝7 ,其中 4x3 + x4 = 9 ⃝8 ⃝7 − ⃝8 ,得同解方程组⃝1 ,⃝2 ,⃝8 ,⃝9 ,其中 x4 = 1 ⃝9 把 x4 代入⃝8 ,得到 x3 = 2.把 x3 代入⃝1 ,得到 x2 = 1.把 x2 代入⃝2 ,得到 x1 = −2. 思考:把已解出的未知数代入某个方程求得其它未知数的过程是否有可能产生“增根”? 定理 1.1. 对于线性方程组的下列操作不改变线性方程组的解. 1. 交换某两个方程在线性方程组中的位置,其它方程不变. 2. 把某个方程替换成它的非零常数倍,其它方程不变. 3. 把某个方程替换成它与另一方程的常数倍之和,其它方程不变. 其中方程 a1x1 + a2x2 + · · · + anxn = b 的常数 λ 倍定义为 (λa1)x1 + (λa2)x2 + · · · + (λan)xn = (λb). 两个方程 a1x1 + a2x2 + · · · + anxn = b 与 a ′ 1x1 + a ′ 2x2 + · · · + a ′ nxn = b ′ 之和定义为 (a1 + a ′ 1 )x1 + (a2 + a ′ 2 )x2 + · · · + (an + a ′ n )xn = (b + b ′ ). 定义 1.1. 以上三类操作,称为对于线性方程组的初等变换.

S1.1消元解法 通过第(③)类初等变换,我们可以消去两个方程所包含的公共未知数.例如,假设第一个方程 含有1,即1≠0,则第一个方程的一1倍与第i个方程之和不含,从而可以得到m-1个 不含1的方程:待由这m-1个方程求得2,·,工n之后,代回第一个方程,解得1.当a1=0 时,某个方程含有x1,第(1)类初等变换可以把方程组化为11≠0情形.第(2)类初等变换则可 以把a11≠0情形化为a1=1情形 例1.1中的同解变形消元过程可以表示为如下初等变换。 酒去 酒去 ③ 】⊙=③-3×@ (@ (⑤-0-⑧ ② (@ =-4×① 0=©-3×① ⑨=0- 定理1.2.线性方程组(11)可以通过一系列初等变换,化为如下阶梯形的线性方程组. ain Tp1+…+dnxn=所 0rn,n+…+dn工n= (1.2) 0=其+1 0=6m 其中0≤r≤min(m,n,1≤pm<2<…<r≤n并且a吃p,…ap.≠0. 证明.对m使用数学归纳法.当m=1时,结论显然成立.当m≥2时,设p是最小的正整数使 得存在即≠0.不妨设1=1,否则交换第i个方程与第1个方程的位置.通过第)类初等变换 利用第1个方程,可以把第2.·,m个方程中x1,·,xm的系数都变成0.对这m一1个方程应 用归纳假设,可以通过一系列初等变换,化为阶梯形的线性方程组.添上第1个方程,仍然是阶梯 形的线性方程组。 定理1.3. 1.钱性方程组(11)有解的充分必要条件是+1=…=m=0 2.线性方程组(1.1)有唯一解的充分必要条件是r=n且1=…=n=0. 证明.把线性方程组(11)变成(12)的初等变换操作不改变方程祖的解
§1.1 消元解法 9 通过第 (3) 类初等变换,我们可以消去两个方程所包含的公共未知数.例如,假设第一个方程 含有 x1,即 a11 6= 0,则第一个方程的 − ai1 a11 倍与第 i 个方程之和不含 x1,从而可以得到 m − 1 个 不含 x1 的方程;待由这 m − 1 个方程求得 x2, · · · , xn 之后,代回第一个方程,解得 x1.当 a11 = 0 时,某个方程含有 x1,第 (1) 类初等变换可以把方程组化为 a11 6= 0 情形.第 (2) 类初等变换则可 以把 a11 6= 0 情形化为 a11 = 1 情形. 例 1.1 中的同解变形消元过程可以表示为如下初等变换. ⃝1 ⃝2 ⃝3 ⃝4 换行 −−→ ⃝2 ⃝1 ⃝3 ⃝4 消去 x1 −−−−→ ⃝2 ⃝1 ⃝3 ⃝5 = ⃝4 − ⃝3 消去 x1 −−−−→ ⃝2 ⃝1 ⃝6 = ⃝3 − 3 × ⃝2 ⃝5 消去 x2 −−−−→ ⃝2 ⃝1 ⃝6 ⃝7 = ⃝5 − 3 × ⃝1 消去 x2 −−−−→ ⃝2 ⃝1 ⃝8 = ⃝6 − 4 × ⃝1 ⃝7 消去 x3 −−−−→ ⃝2 ⃝1 ⃝8 ⃝9 = ⃝7 − ⃝8 定理 1.2. 线性方程组 (1.1) 可以通过一系列初等变换,化为如下阶梯形的线性方程组. a ′ 1p1 xp1 + · · · · · · · · · · · · · · · · · · + a ′ 1nxn = b ′ 1 a ′ 2p2 xp2 + · · · · · · · · · · · · + a ′ 2nxn = b ′ 2 · · · · · · · · · a ′ rpr xpr + · · · + a ′ rnxn = b ′ r 0 = b ′ r+1 . . . 0 = b ′ m (1.2) 其中 0 ⩽ r ⩽ min(m, n),1 ⩽ p1 < p2 < · · · < pr ⩽ n 并且 a ′ 1p1 a ′ 2p2 · · · a ′ rpr 6= 0. 证明. 对 m 使用数学归纳法.当 m = 1 时,结论显然成立.当 m ⩾ 2 时,设 p 是最小的正整数使 得存在 aip 6= 0.不妨设 i = 1,否则交换第 i 个方程与第 1 个方程的位置.通过第 (3) 类初等变换, 利用第 1 个方程,可以把第 2, · · · , m 个方程中 x1, · · · , xp 的系数都变成 0.对这 m − 1 个方程应 用归纳假设,可以通过一系列初等变换,化为阶梯形的线性方程组.添上第 1 个方程,仍然是阶梯 形的线性方程组. 定理 1.3. 1. 线性方程组 (1.1) 有解的充分必要条件是 b ′ r+1 = · · · = b ′ m = 0. 2. 线性方程组 (1.1) 有唯一解的充分必要条件是 r = n 且 b ′ r+1 = · · · = b ′ m = 0. 证明. 把线性方程组 (1.1) 变成 (1.2) 的初等变换操作不改变方程祖的解.

10 第一章钱性方程组 1.若(1.2)有解,则1=…=n=0.若+1=…=n=0,则可以解出工1工m…, 为其它变元的一次函数 2.设1=…=n=0.当r=n时,由(12)的前r个方程,可依次解出x,n-1,…,1, 解是唯一的.当r<n时,设i{p,2,严},则可取任意值,(1.2)的解不唯一.口 习题 1.证明定理1.1. 2.求解下列线性方程组 2m1+2-2x4=1 1-4r%+24=0 1+2-3=1 1+22-2x3=0 2x2-xg-x4=1 x1+2-xg+x4=0 x1+2x2+2xg-2x4=1 x1+32-3z3-x4=0 x1+2-x+26=1 1+x2-2g+2x6=1 x1-3-x4-x5=1 x2-2xg+x4+2z5=1 (3) 2x1-2x2+xg+x4+2x6=1 x1-xg十x4十x5=1 21+2+x-6=1 (1+2-3-2x4+=1 工1+x2-x3+2x4+x6=1 1十x2+x4=-2 x1+3x2+4r4+5x5=1 2z1+2x3-x4=1 (⑤){21+x2-44+54=1 (6){21+x2-xg-4=0 22++24+46=1 1-2-23-2x4=4 21+3x2+3-x4+46=1 2x2-2+x4=-3 3.证明:当m<n且==…=bm=0时,齐次线性方程组(11)必有非零解
10 第一章 线性方程组 1. 若 (1.2) 有解,则 b ′ r+1 = · · · = b ′ m = 0.若 b ′ r+1 = · · · = b ′ m = 0,则可以解出 xp1 , xp2 , · · · , xpr 为其它变元的一次函数. 2. 设 b ′ r+1 = · · · = b ′ m = 0.当 r = n 时,由 (1.2) 的前 r 个方程,可依次解出 xn, xn−1, · · · , x1, 解是唯一的.当 r < n 时,设 i ∈ { / p1, p2, · · · , pr},则 xi 可取任意值,(1.2) 的解不唯一. 习题 1. 证明定理 1.1. 2. 求解下列线性方程组. (1) 2x1 + x2 − 2x4 = 1 x1 + x2 − x3 = 1 2x2 − x3 − x4 = 1 x1 + 2x2 + 2x3 − 2x4 = 1 (2) x1 − 4x3 + 2x4 = 0 x1 + 2x2 − 2x3 = 0 x1 + x2 − x3 + x4 = 0 x1 + 3x2 − 3x3 − x4 = 0 (3) x1 + x2 − x3 + 2x5 = 1 x1 − x3 − x4 − x5 = 1 2x1 − 2x2 + x3 + x4 + 2x5 = 1 2x1 + x2 + x3 − x5 = 1 (4) x1 + x2 − 2x3 + 2x5 = 1 x2 − 2x3 + x4 + 2x5 = 1 x1 − x3 + x4 + x5 = 1 x1 + x2 − x3 − 2x4 + x5 = 1 (5) x1 + x2 − x3 + 2x4 + x5 = 1 x1 + 3x2 + 4x4 + 5x5 = 1 2x1 + x2 − 4x3 + 5x4 = 1 2x2 + x3 + 2x4 + 4x5 = 1 2x1 + 3x2 + 3x3 − x4 + 4x5 = 1 (6) x1 + x2 + x4 = −2 2x1 + 2x3 − x4 = 1 2x1 + x2 − x3 − x4 = 0 x1 − 2x2 − 2x3 − 2x4 = 4 2x2 − 2x3 + x4 = −3 3. 证明:当 m < n 且 b1 = b2 = · · · = bm = 0 时,齐次线性方程组 (1.1) 必有非零解.

S1.2矩阵表示 1.2矩阵表示 在对线性方程组施行初等变换的时候,我们注意到每个方程的左端都是数与字母的乘积之和的 形式,只需要对未知数的系数进行操作:并且方程的个数、未知数的个数、未知数的顺序均保持不 变.因此,我们可以隐去未知数和运算符号,用一个m行n+1列的矩形表格 012 01n 121 02n (1.3) 来表示线性方程组(11),把对于线性方程组的操作转化为对于矩形表格的操作,《九章算术·方程》 中就记拔若这样的解法:用算筹把线性方程组的系数和常数项排成长方形阵,燃后用加减消元法求 解.秦九韶四的《数书九章》(成书于1247年)中则用互乘相消法和代入法求解线性方程组 例1.2.回今有上禾三秉、中禾二秉、下禾一秉,实三十九斗:上禾二秉、中禾三兼、下禾一秉,实 三十四斗:上禾一兼、中禾二兼、下禾三秉,实二十六斗.问上、中、下禾实一秉各几何?答曰:上 禾一秉,九斗、四分斗之一:中禾一秉,四斗、四分斗之一:下禾一秉,二斗、四分斗之三. 方程术曰:置上禾三秉,中禾二秉,下禾一秉,实三十九斗,于右方.中、左行列如右方.以右 行上禾遍乘中行而以直除。又乘其次,亦以直除。然以中行中禾不尽者遍乘左行而以直除.左方丁 禾不尽者,上为法,下为实。实即下禾之实.求中禾,以法乘中行下实,而除下禾之实。余如中禾 秉数而一,即中禾之实,求上禾亦以法乘右行下实,而除下禾、中禾之实,余如上禾秉数而一,即 上禾之实。实皆如法,各得一斗 下面,我们来学习古人的“方程术”.用现代数学的语言来说,原问题等价于求解线性方程组 3x+2y+=39 2x+3y+2=34 x+2u+32=26 首先,把线性方程组的系数按照古人的书写顺序(从上到下,从右到左,行是竖直方向)排成数表。 数表逆时针旋转90°,即为线性方程组的增广矩阵。 左行中行右行 上禾1 23 中禾 2 2 下禾3 1 1 实263439 然后,用(右行,上禾)位置的数3遍乘中行的每个元素,再利用右行对中行消元,得 123 /1631 /103 311 33i 263439/ 2610239/ 262439
§1.2 矩阵表示 11 §1.2 矩阵表示 在对线性方程组施行初等变换的时候,我们注意到每个方程的左端都是数与字母的乘积之和的 形式,只需要对未知数的系数进行操作;并且方程的个数、未知数的个数、未知数的顺序均保持不 变.因此,我们可以隐去未知数和运算符号,用一个 m 行 n + 1 列的矩形表格 M = a11 a12 · · · a1n b1 a21 a22 · · · a2n b2 . . . . . . · · · . . . . . . am1 am2 · · · amn bm (1.3) 来表示线性方程组 (1.1),把对于线性方程组的操作转化为对于矩形表格的操作.《九章算术 · 方程》 中就记载着这样的解法:用算筹把线性方程组的系数和常数项排成长方形阵,然后用加减消元法求 解.秦九韶[1]的《数书九章》(成书于 1247 年)中则用互乘相消法和代入法求解线性方程组. 例 1.2. [2]今有上禾三秉、中禾二秉、下禾一秉,实三十九斗;上禾二秉、中禾三秉、下禾一秉,实 三十四斗;上禾一秉、中禾二秉、下禾三秉,实二十六斗.问上、中、下禾实一秉各几何?答曰:上 禾一秉,九斗、四分斗之一;中禾一秉,四斗、四分斗之一;下禾一秉,二斗、四分斗之三. 方程术曰:置上禾三秉,中禾二秉,下禾一秉,实三十九斗,于右方.中、左行列如右方.以右 行上禾遍乘中行而以直除.又乘其次,亦以直除.然以中行中禾不尽者遍乘左行而以直除.左方下 禾不尽者,上为法,下为实.实即下禾之实.求中禾,以法乘中行下实,而除下禾之实.余如中禾 秉数而一,即中禾之实.求上禾亦以法乘右行下实,而除下禾、中禾之实.余如上禾秉数而一,即 上禾之实.实皆如法,各得一斗. 下面,我们来学习古人的“方程术”.用现代数学的语言来说,原问题等价于求解线性方程组 3x + 2y + z = 39 2x + 3y + z = 34 x + 2y + 3z = 26 首先,把线性方程组的系数按照古人的书写顺序 (从上到下,从右到左,行是竖直方向) 排成数表. 数表逆时针旋转 90◦,即为线性方程组的增广矩阵. 左行 中行 右行 上禾 1 2 3 中禾 2 3 2 下禾 3 1 1 实 26 34 39 然后,用 (右行, 上禾) 位置的数 3 遍乘中行的每个元素,再利用右行对中行消元,得 1 2 3 2 3 2 3 1 1 26 34 39 → 1 6 3 2 9 2 3 3 1 26 102 39 → 1 0 3 2 5 2 3 1 1 26 24 39 . [1]秦九韶,约 1202–1261,南宋著名数学家,四川安岳人. [2]《九章算术》第 8 章《方程》第 1 题.

12 第一章钱性方程组 再对左行作同样的处理,得 262439/ 782439 20420 然后,用(中行,中禾)位置的数5遍乘左行的每个元素,再利用中行对左行消元,得 392439/ 992439 (左行,下禾)位置的数36称为法,(左行,实)位置的数99称为下禾之实.即36秉下禾实99斗, 透亭 =333为上 禾之实.即36秉上禾实333斗. 因此,果上、中,下不之安的斗数分是罗=9行密=号器=号 0 古人的做法几平就是Ga器消元法,先把系数矩阵初等变换成上三角形,再依次回代求解未知 数 在求解过程中,古人始终把运算限制在整数范围内,只是在最后才以分数的形式给出答案究 其原因,古人使用算筹来表示数字,追求计算过程的简洁和精确,与其使用分数,不如先通分,而 后始终在整数范用内运算.事实上,《九章算术》的第一章《方田》中就已经给出了分数的加、减 乘、除、通分、约分运算.分母称为“法”,分子称为“实”例1.2中的“实”,有时指的是“农作 物的收成”,有时指的是“分数的分子”,读者需仔细区分 定义12.(1.3)式中的矩形表格M称为线性方程组(1.1)的增广矩阵.别去M的最后一列得到的 m行n列的矩形表格称为线性方程组(1.1)的系数矩阵。M的第i行从左至右排成的数组,称为 M的第i个行向量.M的第j列从上至下排成的数组,称为M的第j个列向量. 全矩阵的元素并不仅限于数,也可以是含有未知数和字母的代数表达式。 定义1.3.由数域F中的n个数构成的数组=(1,2,…,)称为数域罩上的n维数组向量 简称n维向量,数域丽上所有n维数组向量的集合记作F,元素都是0的向量称为零向量,记作 0.第i个元素是1、其它元素都是0的向量称为第i个标准单位向量,记作e, 设=(1,欢,·,)∈m,入∈R.两个向量的加法运算定义为 工+y=(1+,2+2,…,n+n) 数与向量的数乘运算定义为 Az=(AD1,A2,·,Azn)
12 第一章 线性方程组 再对左行作同样的处理,得 1 0 3 2 5 2 3 1 1 26 24 39 → 3 0 3 6 5 2 9 1 1 78 24 39 → 0 0 3 4 5 2 8 1 1 39 24 39 . 然后,用 (中行, 中禾) 位置的数 5 遍乘左行的每个元素,再利用中行对左行消元,得 0 0 3 4 5 2 8 1 1 39 24 39 → 0 0 3 20 5 2 40 1 1 195 24 39 → 0 0 3 0 5 2 36 1 1 99 24 39 . (左行, 下禾) 位置的数 36 称为法,(左行, 实) 位置的数 99 称为下禾之实.即 36 秉下禾实 99 斗. 下面计算中禾.已知 5 秉中禾、1 秉下禾实 24 斗.用 36 乘 (中行, 实) 位置处的数 24,减去 下禾之实,再除以中禾秉数 5,所得数 36 × 24 − 99 5 = 153 为中禾之实.即 36 秉中禾实 153 斗. 对于上禾,已知 3 秉上禾、2 秉中禾、1 秉下禾实 39 斗.用 36 乘 (右行, 实) 位置处的数 39, 减去下禾之实与 2 倍的中禾之实,再除以上禾秉数 3,所得数 36 × 39 − 99 − 2 × 153 3 = 333 为上 禾之实.即 36 秉上禾实 333 斗. 因此,1 秉上、中、下禾之实的斗数分别是 333 36 = 9 1 4 , 153 36 = 41 4 , 99 36 = 2 3 4 . 古人的做法几乎就是 Gauss 消元法,先把系数矩阵初等变换成上三角形,再依次回代求解未知 数.在求解过程中,古人始终把运算限制在整数范围内,只是在最后才以分数的形式给出答案.究 其原因,古人使用算筹来表示数字,追求计算过程的简洁和精确,与其使用分数,不如先通分,而 后始终在整数范围内运算.事实上,《九章算术》的第一章《方田》中就已经给出了分数的加、减、 乘、除、通分、约分运算.分母称为“法”,分子称为“实”.例 1.2 中的“实”,有时指的是“农作 物的收成”,有时指的是“分数的分子”,读者需仔细区分. 定义 1.2. (1.3) 式中的矩形表格 M 称为线性方程组 (1.1) 的增广矩阵.删去 M 的最后一列得到的 m 行 n 列的矩形表格称为线性方程组 (1.1) 的系数矩阵.M 的第 i 行从左至右排成的数组,称为 M 的第 i 个行向量.M 的第 j 列从上至下排成的数组,称为 M 的第 j 个列向量. 矩阵的元素并不仅限于数,也可以是含有未知数和字母的代数表达式. 定义 1.3. 由数域 F 中的 n 个数构成的数组 x = (x1, x2, · · · , xn) 称为数域 F 上的 n 维数组向量, 简称 n 维向量.数域 F 上所有 n 维数组向量的集合记作 F n.元素都是 0 的向量称为零向量,记作 0.第 i 个元素是 1、其它元素都是 0 的向量称为第 i 个标准单位向量,记作 ei. 设 y = (y1, y2, · · · , yn) ∈ F n,λ ∈ F.两个向量的加法运算定义为 x + y = (x1 + y1, x2 + y2, · · · , xn + yn), 数与向量的数乘运算定义为 λx = (λx1, λx2, · · · , λxn)

S12矩阵表示 13 显然,向量的加法和数乘运算是数的加法和乘法运算的推广,类似地,可定义两个向量的减法运算 E一割=(E1一1,E2一2:···,工n一n 和线性组合运算 证+=(A1+1,2+,…,A江n+n) 并推广为多个向量a1,a2,·,,∈Pm的线性组合运算 X1a1+X202+…+Xk0w 其中4,1,2,…,keF 以下是对于线性方程组(1.1)的两种常见看法. 1.定义两个n维向量x=(c1,2…,)和y=(1,2,,%)的数量积运算为 卫·=工1班+x2欢+…+nn 记n维向量a=(a,a2,…,an).线性方程组(1.1)可以看作是: 。求向量x=(1,2,…,工n)使得a王=,发=1,2,m. 2.记m维向量月=(aa2,am,b=(,2,…,bn.线性方程组(1.1)还可以看作是: 。求线性组合的系数1,2,…,n使得1十x22+…十xnBn=b. 定理14.数组向量的加法和数乘运算具有下列性质. (A1)(x+)+z=x+(y+2) (A2)x+=y+E A3)r+0=0+E=x (A4)x+(-x)=(-x)+x=0 (M1)()z=X() M2)1r= (D1)A(红+)=r+Aw (D2)(入+4)x=λx+x 其中x,,z∈m,入,μ∈F. 线性方程组(1.1)与矩阵M之间存在一一对应关系.方程a11+a22+…+mxn=与 :)一一对应,方程的常数倍对应于行向量的数乘运算,两个方程之和对应 下间的如法运堂对于线性方问作初等衣换的随元是,可以我为对库酸 行向量作初等变换,把M化为阶梯形的矩阵 M'= drp…dn 女 其中M?中空白处的元素都是0
§1.2 矩阵表示 13 显然,向量的加法和数乘运算是数的加法和乘法运算的推广.类似地,可定义两个向量的减法运算 x − y = (x1 − y1, x2 − y2, · · · , xn − yn), 和线性组合运算 λx + µy = (λx1 + µy1, λx2 + µy2, · · · , λxn + µyn), 并推广为多个向量 α1, α2, · · · , αk ∈ F n 的线性组合运算 λ1α1 + λ2α2 + · · · + λkαk 其中 µ, λ1, λ2, · · · , λk ∈ F. 以下是对于线性方程组 (1.1) 的两种常见看法. 1. 定义两个 n 维向量 x = (x1, x2, · · · , xn) 和 y = (y1, y2, · · · , yn) 的数量积运算为 x · y = x1y1 + x2y2 + · · · + xnyn. 记 n 维向量 αi = (ai1, ai2, · · · , ain).线性方程组 (1.1) 可以看作是: • 求向量 x = (x1, x2, · · · , xn) 使得 αi · x = bi,∀i = 1, 2, · · · , m. 2. 记 m 维向量 βj = (a1j , a2j , · · · , amj ),b = (b1, b2, · · · , bm).线性方程组 (1.1) 还可以看作是: • 求线性组合的系数 x1, x2, · · · , xn 使得 x1β1 + x2β2 + · · · + xnβn = b. 定理 1.4. 数组向量的加法和数乘运算具有下列性质. (A1) (x + y) + z = x + (y + z) (A2) x + y = y + x (A3) x + 0 = 0 + x = x (A4) x + (−x) = (−x) + x = 0 (M1) (λµ)x = λ(µx) (M2) 1x = x (D1) λ(x + y) = λx + λy (D2) (λ + µ)x = λx + µx 其中 x, y, z ∈ F n,λ, µ ∈ F. 线性方程组 (1.1) 与矩阵 M 之间存在一一对应关系.方程 ai1x1 + ai2x2 + · · · + ainxn = bi 与 行向量 (ai1, ai2, · · · , ain, bi) 一一对应,方程的常数倍对应于行向量的数乘运算,两个方程之和对应 于两个行向量的加法运算.对于线性方程组 (1.1) 作初等变换的消元过程,可以表示为对矩阵 M 的 行向量作初等变换,把 M 化为阶梯形的矩阵 M′ = a ′ 1p1 · · · · · · · · · · · · · · · · · · a ′ 1n b ′ 1 a ′ 2p2 · · · · · · · · · · · · a ′ 2n b ′ 2 · · · · · · · · · . . . . . . a ′ rpr · · · a ′ rn b ′ r b ′ r+1 . . . b ′ m 其中 M′ 中空白处的元素都是 0.
14 第一章钱性方程组 例1.3.用矩阵方法求解例1.1. 解答。 /01 -10-1Y /1-200 -200-4 -200-4 交换①.回, 01-10 01-10-1 3-201- 3-201 _7 8 04015 8号 1 3 0 3 13 12 -2 00-4 1 -2 0 0 -4 1-200-4 0 0 0=-2回 01 -10- ③-③ 00 419 00419 00408 00 8319/ 0001 1 0001 1 -2 00 4 1 -200 /1000-2 0 -10 ②+=®01001 ①+=2 0100 00 10 2 00102 00102 00011 00011 00011 上式最后一个矩阵的最后一列即为方程组的解,(任1,x2,正3,x4)=(-2,1,2,1). 习题 1.证明定理1.4. 2.用矩阵方法求解$11习题2. 3.设A(1,0),B(0,2),C(3,3).求△ABC的外接圆方程. 4.设A(L,0,),B(0,2,0),C(0,0,3).求△ABC的外接圆方程. 5.求满足f)=f2)=f3)=1,f(-1)=f(-2)=f(-3)=-1的所有多项式f) 6.求满是f)=P)="()=1,f(-1)=(-1)=f"(-1)=-1的所有多项式f(x) 7.当入取何值时,如下线性方程组有解?有唯一解?并求其所有解 Ar1+2+x4=1 +2+x=1 购+A+4=1 21+z+A4=1 8.当α,b取何值时,如下线性方程组有解?有唯一解?并求其所有解 [ar+z2+z3+=0 2x1-x2+2x3+3x4=b 2x1+x2-xg+2x4=1 2++24=1 2+23+3r4=2
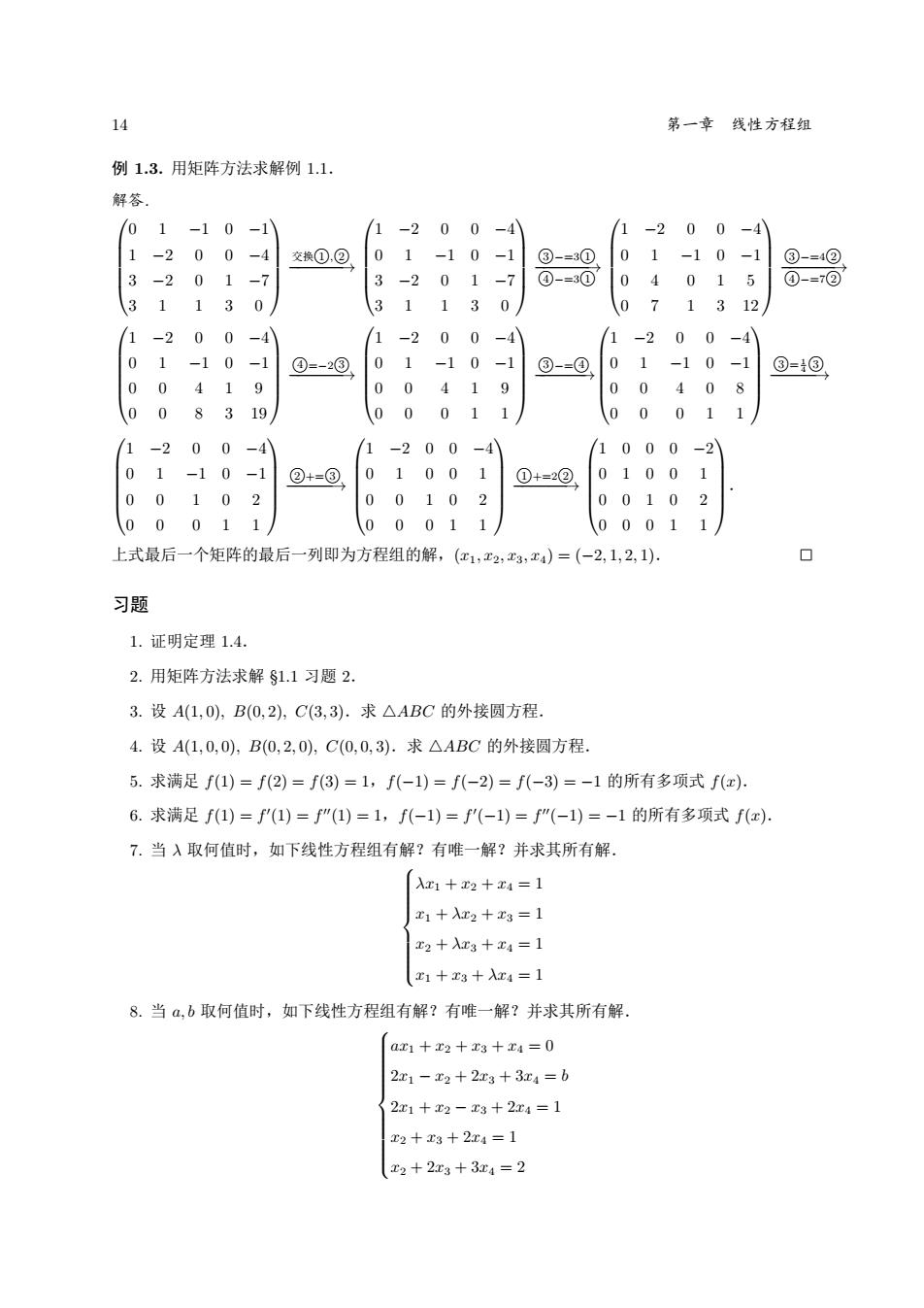
14 第一章 线性方程组 例 1.3. 用矩阵方法求解例 1.1. 解答. 0 1 −1 0 −1 1 −2 0 0 −4 3 −2 0 1 −7 3 1 1 3 0 交换⃝1 ,⃝2 −−−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 3 −2 0 1 −7 3 1 1 3 0 ⃝3 −=3⃝1 −−−−−−→ ⃝4 −=3⃝1 1 −2 0 0 −4 0 1 −1 0 −1 0 4 0 1 5 0 7 1 3 12 ⃝3 −=4⃝2 −−−−−−→ ⃝4 −=7⃝2 1 −2 0 0 −4 0 1 −1 0 −1 0 0 4 1 9 0 0 8 3 19 ⃝4 =−2⃝3 −−−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 0 0 4 1 9 0 0 0 1 1 ⃝3 −=⃝4 −−−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 0 0 4 0 8 0 0 0 1 1 ⃝3 = 1 4⃝3 −−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 0 0 1 0 2 0 0 0 1 1 ⃝2 +=⃝3 −−−−−→ 1 −2 0 0 −4 0 1 0 0 1 0 0 1 0 2 0 0 0 1 1 ⃝1 +=2⃝2 −−−−−−→ 1 0 0 0 −2 0 1 0 0 1 0 0 1 0 2 0 0 0 1 1 . 上式最后一个矩阵的最后一列即为方程组的解,(x1, x2, x3, x4) = (−2, 1, 2, 1). 习题 1. 证明定理 1.4. 2. 用矩阵方法求解 §1.1 习题 2. 3. 设 A(1, 0), B(0, 2), C(3, 3).求 4ABC 的外接圆方程. 4. 设 A(1, 0, 0), B(0, 2, 0), C(0, 0, 3).求 4ABC 的外接圆方程. 5. 求满足 f(1) = f(2) = f(3) = 1,f(−1) = f(−2) = f(−3) = −1 的所有多项式 f(x). 6. 求满足 f(1) = f ′ (1) = f ′′(1) = 1,f(−1) = f ′ (−1) = f ′′(−1) = −1 的所有多项式 f(x). 7. 当 λ 取何值时,如下线性方程组有解?有唯一解?并求其所有解. λx1 + x2 + x4 = 1 x1 + λx2 + x3 = 1 x2 + λx3 + x4 = 1 x1 + x3 + λx4 = 1 8. 当 a, b 取何值时,如下线性方程组有解?有唯一解?并求其所有解. ax1 + x2 + x3 + x4 = 0 2x1 − x2 + 2x3 + 3x4 = b 2x1 + x2 − x3 + 2x4 = 1 x2 + x3 + 2x4 = 1 x2 + 2x3 + 3x4 = 2