
第九章一维搜索 从这一章开始,我们来研究非线性规划的具体算法.本章主要 讨论一维搜索,它是后面各章将要介绍的各种计算过程的重要组 成部分.在实际应用中,一维搜索不仅需要大量时机,而且它的选 择是否恰当对一些算法的计算效果有重要影响, §9.1一维搜索概念 9.1.1 什么是一维搜索 在许多迭代下降算法中,具有一个共同点,这就是得到点x (k) 后,需要按某种规则确定一个方向),再从xk)出发,沿方向x) 在直线(或射线)上求目标函数的极小点,从而得到)的后xk+) .重复以上做法,直至求得问题的解这里所谓求目标函数 在直线上的极小点,称为一维搜索,或称为线搜索:
第九章 一维搜索 从这一章开始,我们来研究非线性规划的具体算法.本章主要 讨论一维搜索,它是后面各章将要介绍的各种计算过程的重要组 成部分.在实际应用中,一维搜索不仅需要大量时机,而且它的选 择是否恰当对一些算法的计算效果有重要影响. §9.1 一维搜索概念 9.1.1 什么是一维搜索 在许多迭代下降算法中,具有一个共同点,这就是得到点 后,需要按某种规则确定一个方向 ,再从 出发,沿方向 在直线(或射线)上求目标函数的极小点,从而得到 的后 点 .重复以上做法,直至求得问题的解.这里所谓求目标函数 在直线上的极小点,称为一维搜索,或称为线搜索. (k ) x (k ) d (k ) x (k ) x (k ) x (k +1) x

一维搜索可归结为单变量函数的极小化问题.设目标函数为 f(x),过点x“沿方向dk的直线可用点集来表示,记作 L={xx=x(k)+id(),-oo<A<co} (9.1.1) 求(x在直线工上的极小点转化为求一元函数 p(2)=f(x)+dk) (9.1.2) 的极小点 如果p(2)的极小点为2,通常称2为沿方向d)的步长因子, 或简称为步长,那么函数f(x)在直线L上的极小点就是 xk+)=xk)+元d) (9.1.3) 一维搜索的方法很多,归纳起来,大体可分成两类:
一维搜索可归结为单变量函数的极小化问题. 设目标函数为 f (x) ,过点 x (k ) 沿方向 d (k ) 的直线可用点集来表示,记作 { | , } ( ) ( ) = = + − k k L x x x d (9.1.1) 求 f (x) 在直线 L 上的极小点转化为求一元函数 ( ) ( ) (k ) (k ) = f x + d (9.1.2) 的极小点. 如果 的极小点为 ,通常称 为沿方向 的步长因子, 或简称为步长,那么函数 在直线 上的极小点就是 () k k (k ) d f (x) L ( 1) ( ) (k ) k k k x = x + d + (9.1.3) 一维搜索的方法很多,归纳起来,大体可分成两类:

一类是试探法.采用这类方法,需要按某种方式找试探点,通 过一系列试探点来确定极小点, 另一类是函数逼近法,或称插值法.这类方法是用某种较简 单的曲线逼近本来的函数曲线,通过求逼近函数的极小点来估 计目标函数的极小点 这两类方法一般只能求得极小点的近似值. 在一维搜索中,可能出现这样情形:在直线上存在多个极小点 这时可采取不同策略.可以选择第一个极小点,也可以从中选择最 小点,甚至还可以从这若干个极小点中任意选择一个,只要这点的 函数值不超过在点xk)的目标函数值即可
一类是试探法.采用这类方法,需要按某种方式找试探点,通 过一系列试探点来确定极小点. 另一类是函数逼近法,或称插值法. 这类方法是用某种较简 单的曲线逼近本来的函数曲线, 通过求逼近函数的极小点来估 计目标函数的极小点. 这两类方法一般只能求得极小点的近似值. 在一维搜索中,可能出现这样情形:在直线上存在多个极小点. 这时可采取不同策略.可以选择第一个极小点,也可以从中选择最 小点,甚至还可以从这若干个极小点中任意选择一个,只要这点的 函数值不超过在点 的目标函数值即可. (k ) x

§9.2 试探法 9.2.10.618法黄金分割法) 0.618法使用于单峰函数,为阐述0.618法的原理,需要引入单 峰函数的概念. 定义9.2.1设∫是定义在闭区间[a,b]上的一元实函数,x是 f在[a,b]上的极小点,并且对任意的x,x2)∈[a,b]x①f(x2) 当r≤x时,f(x2)>f(x) 则称∫是在闭区间[a,b]上的单峰函数. 单峰函数具有一个很有用的性质:通过计算区间[α,b]内二 个不同点处的函数值,就能确定一个包含极小点的子区间
§9.2 试探法 9.2.1 0.618法(黄金分割法) 0.618法使用于单峰函数, 为阐述0.618法的原理, 需要引入单 峰函数的概念. 定义9.2.1 设 是定义在闭区间 上的一元实函数, 是 在 上的极小点,并且对任意的 , , 有 f [a,b] [a,b] x f , [ , ] (1) (2) x x a b (1) (2) x x , ( ) ( ) (2) (1) (2) 当x x时 f x f x , ( ) ( ) (1) (2) (1) 当x x 时 f x f x 则称 是在闭区间 上的单峰函数. f [a,b] 单峰函数具有一个很有用的性质:通过计算区间 内二 个不同点处的函数值,就能确定一个包含极小点的子区间. [a,b]

定理9.2.1设f是区间[a,b]上的单峰函数x四,x2e女,b], 且xDf(x2),则对每一个x∈[a,x],有 f(x)>f(x2);如果 f(x)≤f(x2) 则对每一个x∈[x2,b],有f(x)≥f(x). 0.618法的基本思想是:根据上述定理,通过取试探点使包含 极小点的区间(不确定区间)不断缩短,当区间长度小到一定程度 时,区间上各点的函数值均接近极小值,因此任意一点都可作为极 小点的近似 综上所述,运用0.618法,初始搜索区间记作[α1,b],第1次迭代 取两个试探点2和山,以后每次迭代中,只需按照公式新计算一点 详细计算步骤如下:
定理9.2.1 设 是区间 上的单峰函数, , f [a,b] , [ , ] (1) (2) x x a b 且x (1) x (2) 。如果f (x (1) ) f (x (2) ),则对每一个x [a, x (1) ],有 f (x) f (x (2) );如果( ) ( ) (1) (2) f x f x 则对每一个 [ , ] ,有 . (2) x x b ( ) ( ) (1) f x f x 0.618法的基本思想是:根据上述定理,通过取试探点使包含 极小点的区间(不确定区间)不断缩短,当区间长度小到一定程度 时,区间上各点的函数值均接近极小值,因此任意一点都可作为极 小点的近似. 综上所述,运用0.618法,初始搜索区间记作 ,第1次迭代 取两个试探点 ,以后每次迭代中,只需按照公式新计算一点. 详细计算步骤如下: [ , ] a1 b1 1和1

1.置初始区间[a1,b]及精度要求L>0,计算试探点24,计 算函数值f()和f(4).计算公式是: 入=a1+0.382(b-a) 41=41+0.618(b-41) 令k=1· 2若bk-akf4)时,转步3; 当f(2)≤f(4)时,转步4. 3.置ak1=九k,bk+1=bk,人k+1=4k, 4k+1=ak+1+0.618(bk+1-ak+1)) 计算函数值f(4k+1),转步5
1.置初始区间 及精度要求 ,计算试探点 ,计 算函数值 .计算公式是: [ , ] a1 b1 L 0 1 和1 ( ) ( ) 1 1 f 和f 0.382( ) 1 = a1 + b1 − a1 0.618( ) 1 = a1 + b1 − a1 令 k =1 . 2.若 ,则停止计算.否则,当 时,转步3; 当 时,转步4. bk − ak L ( ) ( ) k k f f ( ) ( ) k k f f 3.置 , , , ak+1 = k bk+1 = bk k+1 = k 0.618( ) k+1 = ak+1 + bk+1 − ak+1 计算函数值 ,转步5. ( ) k+1 f

4.置ak+1=ak,bk+1=4k,4k+1=九k, 元k+1=ak+1+0.382(bk+1-ak+1) 计算函数值f(2+),转步5. 5.置k:=k+1,返回步2. 例9.2.1 用0.618法解下列问题: min f(x)=2x2-x-1 初始区间[a1,b]=[-1,1],精度L≤0.16 前面已经指出,0.618法使用于单峰函数.但是,在实际问题中, 目标函数在其定义域内不一定是单峰的,因此需要先确定单峰区 间,然后再使用0.618法的计算公式.在现有的0.618法的程序中,一 般具有这种功能
计算函数值 ,转步5. , , , 4.置 ak+1 = ak bk+1 = k k+1 = k 0.382( ) k+1 = ak+1 + bk+1 − ak+1 ( ) k+1 f 5.置 k := k +1 ,返回步2. 例9.2.1 用0.618法解下列问题: min ( ) 2 1 2 = − − f x x x 初始区间 [a1 ,b1 ] =[−1,1] ,精度 L 0.16 前面已经指出,0.618法使用于单峰函数.但是,在实际问题中, 目标函数在其定义域内不一定是单峰的,因此需要先确定单峰区 间,然后再使用0.618法的计算公式.在现有的0.618法的程序中,一 般具有这种功能

例9.2.2用0.618法求函数f(x)=x2-6x+2的在区 间[0,10]上近似极小点,6=0.3。 解:令=0,b=10,则最初的两个探索点为 2=0+0.382(10-0)=3.82 4=0+0.618(10-0)=6.18 f(2)=-6.328,f(4)=3.112, 因f()<f(4)故得到新区间0,6.18,该区间上 的保留点为42=人=3.28,元=0+6.18-3.82=2.36。 重复以上过程,计算结果如表1
例9.2.2 用0.618法求函数 2 f x x x ( ) 6 2 = − + 1 = + − = 0 0.382(10 0) 3.82 = 0.3。 1 = + − = 0 0.618(10 0) 6.18 1 1 f f ( ) ( ), 1 1 f f ( ) 6.328, ( ) 3.112, = − = 2 1 = = 3.28, 2 = + − = 0 6.18 3.82 2.36。 的在区 间[0,10]上近似极小点, 解:令a=0,b=10, 则最初的两个探索点为 因 故得到新区间[0,6.18],该区间上 的保留点为 重复以上过程,计算结果如表1
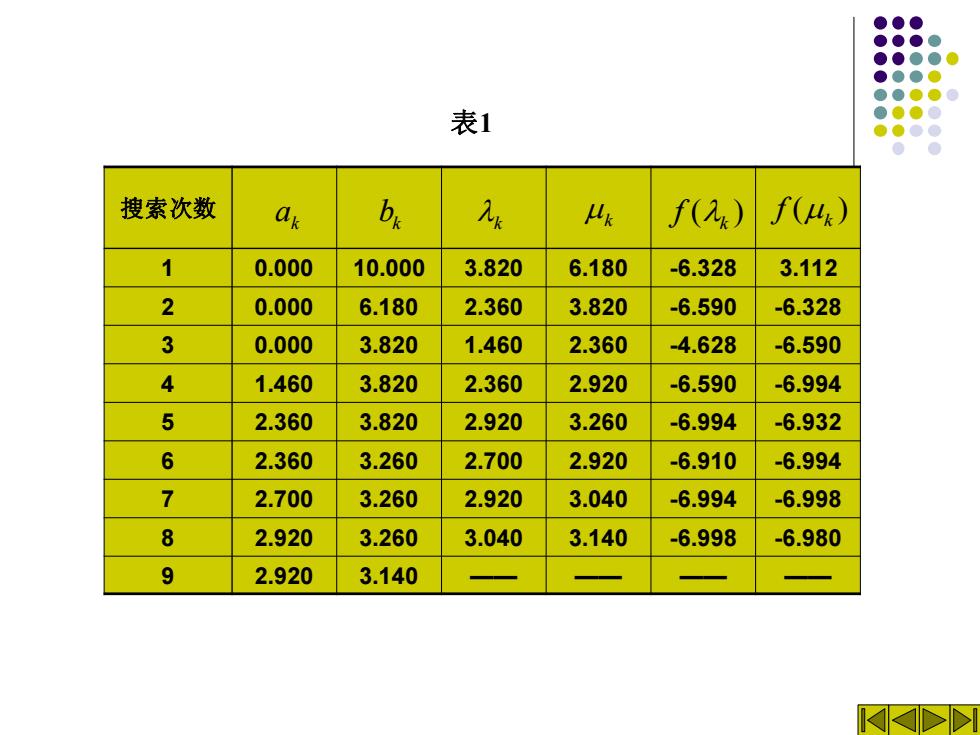
表1 搜索次数 b元 凸k f() f(4) 1 0.000 10.000 3.820 6.180 -6.328 3.112 2 0.000 6.180 2.360 3.820 -6.590 -6.328 3 0.000 3.820 1.460 2.360 -4.628 -6.590 4 1.460 3.820 2.360 2.920 -6.590 -6.994 5 2.360 3.820 2.920 3.260 -6.994 -6.932 6 2.360 3.260 2.700 2.920 -6.910 -6.994 7 2.700 3.260 2.920 3.040 -6.994 -6.998 8 2.920 3.260 3.040 3.140 -6.998 -6.980 9 2.920 3.140
表1 搜索次数 1 0.000 10.000 3.820 6.180 -6.328 3.112 2 0.000 6.180 2.360 3.820 -6.590 -6.328 3 0.000 3.820 1.460 2.360 -4.628 -6.590 4 1.460 3.820 2.360 2.920 -6.590 -6.994 5 2.360 3.820 2.920 3.260 -6.994 -6.932 6 2.360 3.260 2.700 2.920 -6.910 -6.994 7 2.700 3.260 2.920 3.040 -6.994 -6.998 8 2.920 3.260 3.040 3.140 -6.998 -6.980 9 2.920 3.140 —— —— —— —— k a ( ) k ( ) f k bk k k f

因为 b-a=0.22>
因为 ( ) * x b a = + = 9 9 2 3.03 b a 9 9 − = 0.22 0.3 所以迭代终止。此时,取近似最优解为