
第四章对偶理论及灵敏度分析 线性规中的对偶理论 对偶单纯形法 ◆灵敏度分析
第四章 对偶理论及灵敏度分析 ◆ 线性规划中的对偶理论 ◆对偶单纯形法 ◆灵敏度分析
§1线性规划的对偶理论 一、对偶问题的实例 产品 资源 maxz=1500x1+2500x2 资源 甲 乙 限制 A 3 2 65 s.t. 3x1+2x2≤65 B 2 1 40 2x1+x2≤40 (1) C 0 3 75 3x2≤75 单件利润 1500 2500 X1,x2≥0 最优解为:x1*=5,x2* 如果称(1)为LP问题的 设y,y23分别为A,B,C 原问题,则称(2)为(1) min w=65y1+40y2+75y3的对偶问题。 s.t. 3y1+2y2 ≥1500(2) 最优解为:y1*=500 2y1+y2+3y3≥2500 y2*=0,y3*=500, y1,y2,y3≥0 wmin=70000
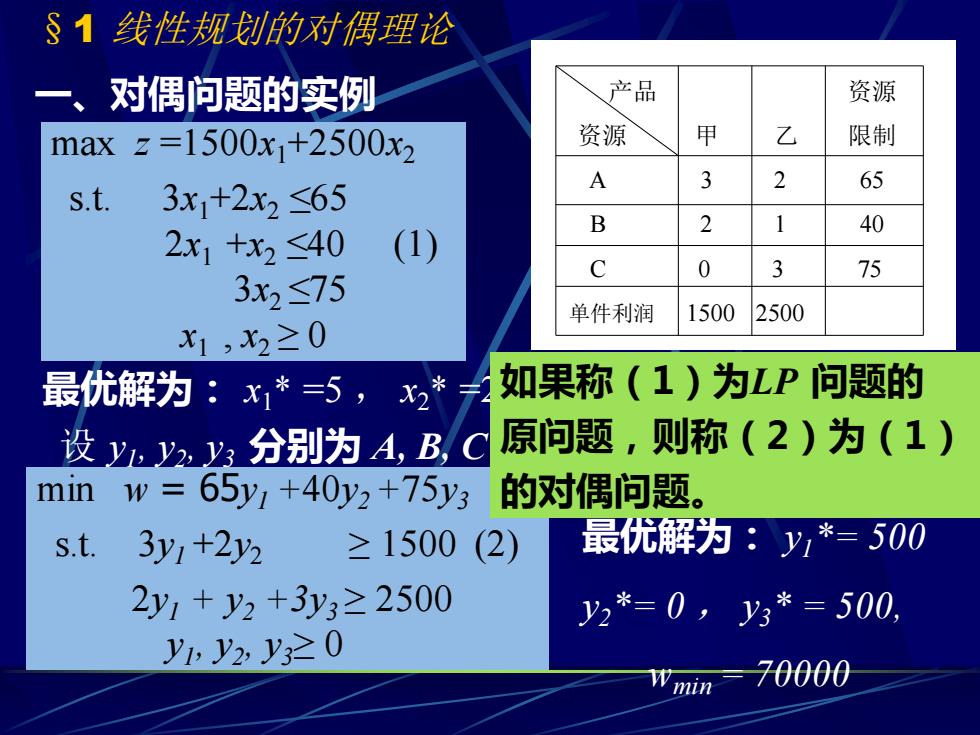
§1 线性规划的对偶理论 一、对偶问题的实例 产品 资源 资源 甲 乙 限制 A 3 2 65 B 2 1 40 C 0 3 75 单件利润 1500 2500 max z =1500x1+2500x2 s.t. 3x1+2x2 ≤65 2x1 +x2 ≤40 (1) 3x2 ≤75 x1 , x2 ≥ 0 最优解为: x1* =5 , x2* =25 zmax =70000 设 y1 , y2 , y3 分别为 A, B, C 三种资源出售的价格 3y1 +2y2 ≥ 1500 2y1 + y2 +3y3 ≥ 2500 w= 65y1 +40y2 +75y3 min w = 65y1 +40y2 +75y3 s.t. 3y1 +2y2 ≥ 1500 (2) 2y1 + y2 +3y3 ≥ 2500 y1 , y2 , y3≥ 0 最优解为: y1*= 500 y2*= 0 , y3* = 500, wmin = 70000 如果称(1)为LP 问题的 原问题,则称(2)为(1) 的对偶问题

第四章对偶理论及灵敏度分析 二、对偶问题 min i=cx max y=w b P s.tAx≥b D) s.twA≤C 1、对称型对 x≥0 定义1设原LP问题为 则称下列XP问题 minz=C心+CX2+..+Crxn max y=biw+b2w2+...+bmwm s.t. 01心1+4122+..+01xn≥b1 s.t. a21+422x2+..+a2mxn≥b2 an"1+a2nW2+.…+amwm≤C1 aw+a2w2+...+am2wmc2 4) amam2X2+…+amn≥bm ≥0G=1,2,.,n)) a1nw1+a2nw2+…+AmnWm≤Cn 为其对偶问题,其中 w,≥0(=1,2,,m)称为对偶变量 并称(3)、(4)为一对对称型对偶问题
第四章 对偶理论及灵敏度分析 二、对偶问题的形式 1、对称型对偶问题 min z = c1 x1 + c2 x2 + … + cn xn s.t. a11x1 + a12x2 + … + a1nxn ≥ b1 a21x1 + a22x2 + … + a2nxn ≥ b2 (3) … … am1x1 + am2x2 + … + amnxn ≥ bm xj ≥ 0 (j = 1,2,…,n) max y = b1 w1 + b2 w2 + … +bm wm s.t. a11w1 + a21 w2 + … + am1wm ≤ c1 a12w1 + a22w2 + … + am2 wm ≤ c2 (4) … … a1nw1 + a2nw2 + … + amnwm ≤ cn wi≥ 0 (i = 1,2,…,m) 定义1 设原 LP 问题为 则称下列 LP 问题 为其对偶问题,其中 wi ≥ 0 (i = 1,2,…,m)称为对偶变量, 并称(3)、(4)为一对对称型对偶问题 min z=cx (P) s.t. Ax ≥ b x ≥ 0 max y= w b (D) s.t. w A ≤ c w ≥ 0
§1线性规的对偶理论 2、非对称型对偶问题 maxy=wb D】cA≤C min =cx max y=wb P s.t.Ax=b D s.twA≤ c x≥0 w无符号限制 引入对偶变量 (u,v),其中u=(u,42,,4m) min =cx S.t.Ax≥b 为对应于第一组不等式约束A化≥b的对偶变 -Ax≥-b 量,y=(y,y,ym)为对应于第二组不等式约 x≥0 束-Ax≥-b的对偶变量,按对称型的结论: max y=(u,v) 6 max y=(u-v)b s.t(u-)A≤c 令w=u-y s.t. (u,) A ≤C (-A 4,v≥0 u,v≥0
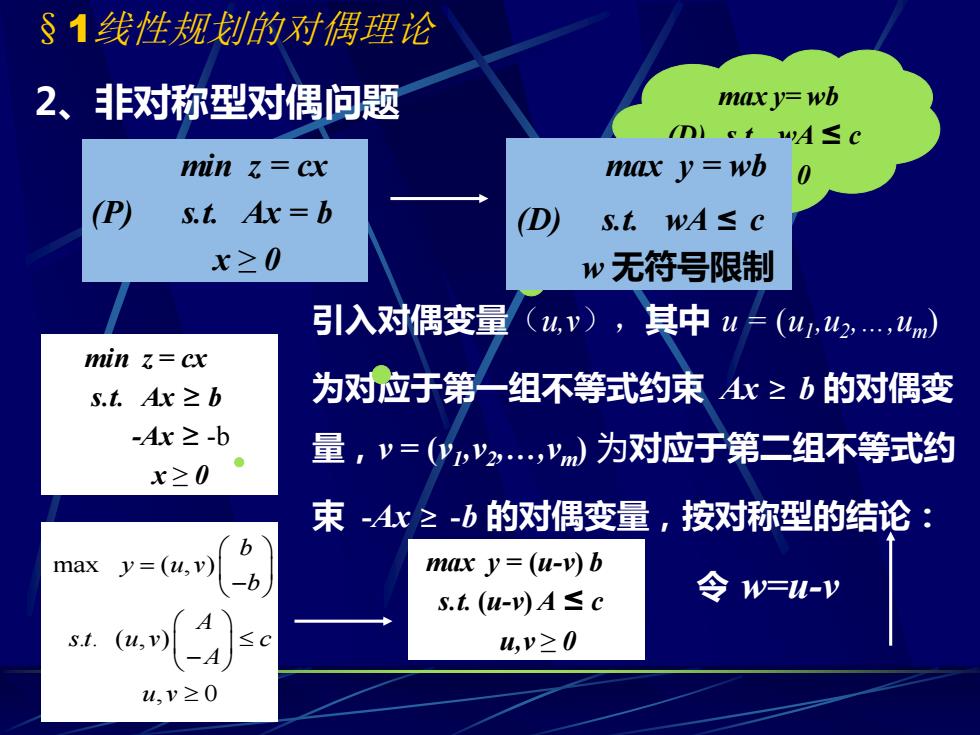
§1线性规划的对偶理论 2、非对称型对偶问题 min z = cx (P) s.t. Ax = b x ≥ 0 min z = cx s.t. Ax ≥ b -Ax ≥ -b x ≥ 0 引入对偶变量(u,v),其中 u = (u1 ,u2 ,…,um) 为对应于第一组不等式约束 Ax ≥ b 的对偶变 量,v = (v1 ,v2 ,…,vm) 为对应于第二组不等式约 束 -Ax ≥ -b 的对偶变量,按对称型的结论: max ( , ) . . ( , ) , 0 b y u v b A s t u v c A u v = − − max y = (u-v) b s.t. (u-v) A ≤ c u,v ≥ 0 令 w=u-v max y= wb (D) s.t. wA ≤ c max y = wbw ≥ 0 (D) s.t. wA ≤ c w 无符号限制

第四章对偶理论及灵敏度分析 3、一般情形 min cx max P)s.tAx≥b wb +w2b +wb A Axx=b2 -Im 0 S.t.(w1,w2,w3) 0 0 ≤(c,0,0) A3x≤b3 A 0 20, 化原问题为标准型: max y=bw+b2w2+b3W; min =cx 按非对 s.t.WAj+W2A2+w:A:sc s.t.Apx-xs =b1 Axx =b2 称型 w1≥0 AX+比 =b3 w3≤0 w2无限制 x,x,X≥0
第四章 对偶理论及灵敏度分析 3、一般情形 min z = cx (P) s.t. A1x ≥ b1 A2x = b2 A3x ≤ b3 x≥ 0, 其中 Ai 为mi× n 矩阵;bi 为mi维列向量;c为n维行 向量;x为n 维列向量, i=1,2,3 化原问题为标准型: min z = cx s.t. A1x- xs = b1 A2x = b2 A3x+xt = b3 x , xs , xt ≥ 0 max y = b1 w1+b2w2 +b3w3 s.t. w1 A1+w2 A2+w3 A3 ≤ c w1 ≥ 0 w3 ≤ 0 w2 无限制 按非对 称型 1 3 1 1 2 2 3 3 min 0 0 0 . . 0 0 0 , , 0 s t m s m t s t cx x x A I x b s t A x b A I x b x x x + + − = 1 3 1 1 2 2 3 3 1 1 2 3 2 3 max 0 . . ( , , ) 0 0 ( ,0,0) 0 m m w b w b w b A I s t w w w A c A I + + −
§1线性规的对偶理论 eg.1写出(P)问题 原问题与对偶问题的关系 的(D)问题 原问题 对偶问题 max z=2x+3x2-5x3+x 目标函数min 目标函数max S.t.4x+x2-3x3+2x4≥5 m个 m个 3x-2x2+7x4≤4 约束条件 ≥0 变 -2x1+3x2+43+x4=6 ≤ ≤0 量 x1≤0,x2,x3≥0,x4无符号限制 无符号限制 n个 n个 inw=5y1+4y3+0y3 变 ≥0 ≤ s.t. 4y1+3y2-2y3≤2 量 ≤0 约束条件 y1-2y2+3y3≥3 无符号限制 -3y1+4y3≥-5 目标函数的系数 约束条件右端常数 约束条件右端常数 目标函数的系数 2y1+7y2+y3=1 1≤0,y2≥0,y3无符号限制
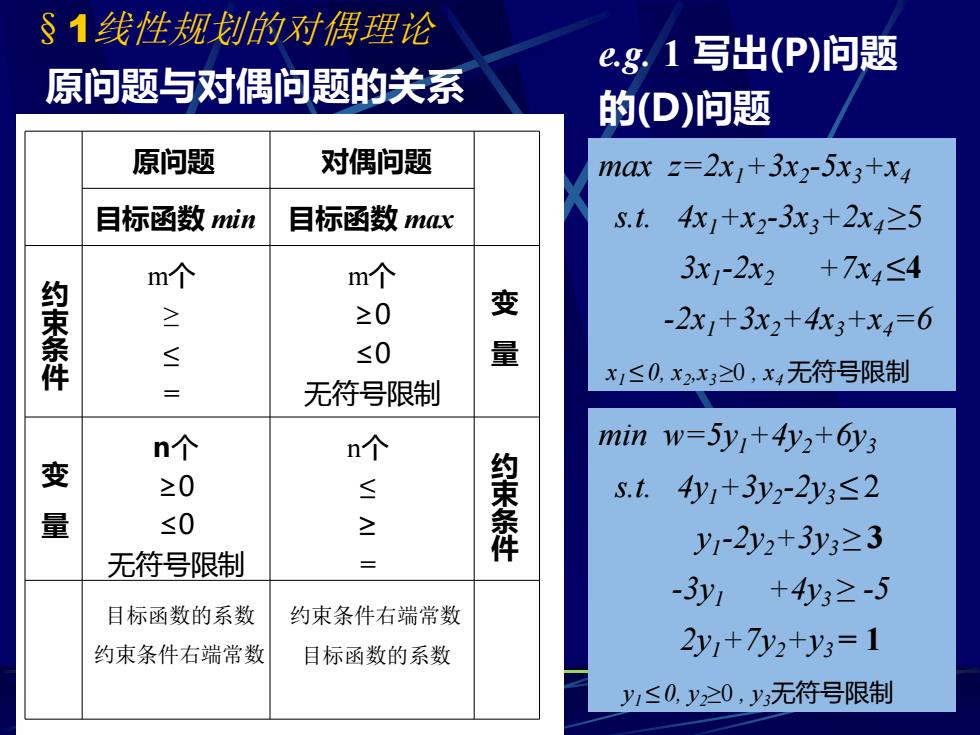
§1线性规划的对偶理论 原问题与对偶问题的关系 原问题 目标函数 min 目标函数 max m个 ≥ ≤ = n个 ≤ ≥ = n个 ≥0 ≤0 无符号限制 m个 ≥0 ≤0 无符号限制 目标函数的系数 约束条件右端常数 约束条件右端常数 目标函数的系数 约 束 条 件 约 束 条 件 变 量 变 量 对偶问题 e.g. 1 写出(P)问题 的(D)问题 max z=2x1+3x2 -5x3+x4 s.t. 4x1+x2 -3x3+2x4 ≥5 3x1 -2x2 +7x4 ≤4 -2x1+3x2+4x3+x4=6 x1 ≤ 0, x2 ,x3 ≥0 , x4 无符号限制 min w=5y1+4y2+6y3 s.t. 4y1+3y2 -2y3 ≤ 2 y1 -2y2+3y3 ≥ 3 -3y1 +4y3 ≥ -5 2y1+7y2+y3 = 1 y1 ≤ 0, y2≥0 , y3无符号限制

§1线性规的时偶理论 (P)问题 D 问题 讨论对称形式: min =cx x y=wb s.tAx≥b s.t wA≤C x≥0 w≥0 对偶规划的若干定理 互为对偶 Theorem 1 (对称性定理)对偶问题的对偶是原问题, proof Theorem 2 (弱对偶定理)设x和w0分别是(P)问题和 (D)问题的可行解,则必有 cxW≥w0b proof Corollary1如果x*和w分别是(P)问题和(D)问 题的可行解,且cx=w*b,则x*和w分别是(P)问 题和(D)问题的最优解: 向前
§1 线性规划的对偶理论 讨论对称形式: (P)问题 min z = cx s.t. Ax ≥ b x ≥0 (D)问题 max y= wb s.t. wA ≤ c w ≥0 一、对偶规划的若干定理 Theorem 1 (对称性定理) 对偶问题的对偶是原问题. 互为对偶 proof Theorem 2 (弱对偶定理) 设 x 0 和 w0 分别是(P)问题和 (D)问题的可行解,则必有 c x0 ≥ w0 b . Corollary 1 如果 x * 和 w* 分别是(P)问题和(D)问 题的可行解,且c x * = w* b,则 x * 和 w* 分别是(P)问 题和(D)问题的最优解。 proof 向前

§1线性规的对偶理论 (D)问题 Theorem (对称性定理) max y=wb proof: 先将(D)问题化成原问题形式 s.t wA≤C w≥0 min y=(-b")w s.t. (4)w≥ ≥0 设x为它的对偶变量,写出它的对偶问题 max z =x"(-c") 即 min z=Cx s.tx(-A)≤-b S.t.Ax≥b x≥0 x≥0 这就是(P)问题. 证些
§1 线性规划的对偶理论 Theorem 1 (对称性定理) proof : 先将(D)问题化成原问题形式 min ( ) . . ( ) 0 T T T T T T y b w s t A w c w = − − − (D)问题 max y = wb s.t. wA ≤ c w ≥0 设 x T为它的对偶变量, 写出它的对偶问题 max ( ) . . ( ) 0 T T T T T T z x c s t x A b x = − − − min . . 0 z cx s t Ax b x = 即 这就是(P)问题. 证毕

§1线性规的对偶理论 cx0≥wWb Theorem 2 (弱对偶定理 proof: 因为x是P)问题的可行解,故必有 A4x0≥b,x0≥0 (1 又w是问题(D)的可行解,于是有 w0A≤c,w0≥0 用w0左乘不等式(1)两边,得 w0AxW≥w0b 用x0右乘不等式(2)两边,得 w0AxW≤Cx0 工上 从而有 cxwob I三
§1 线性规划的对偶理论 Theorem 2 (弱对偶定理) proof : 因为 x 0 是(P)问题的可行解, 故必有 Ax 0 ≥ b , x 0 ≥0 (1) 又w0是问题(D)的可行解, 于是有 w0A ≤ c , w0 ≥0 (2) 用w0 左乘不等式 (1) 两边, 得 w0Ax0 ≥ w0b 用x 0 右乘不等式 (2) 两边, 得 w0Ax0 ≤ cx0 从而有 cx0 ≥ w0b 证毕 c x0 ≥ w0 b

第四章对偶理论及灵敏度分析 Corollary2在一对对偶问题中,如果其中一个问题可 行,但目标函数无界,则另一个问题不可行 Corollary3一对对偶问题(P) 和(D)有最优解的充 要条件是它们同时有可行解 Theorem 3 (对偶定理) 如果(P)问题((D) 问题)有 最优解,那么(D)问题((P)问题)也有最优解 且目标函数值相等。 proof Corollary 4 (单纯形乘子定理) 如果(P)问题有最优解 最优基为B,则w*=CBI就是(D)问题的一个最优 解 向前
第四章 对偶理论及灵敏度分析 Corollary 2 在一对对偶问题中,如果其中一个问题可 行,但目标函数无界,则另一个问题不可行。 Corollary 3 一对对偶问题(P)和(D)有最优解的充 要条件是它们同时有可行解。 Theorem 3 (对偶定理) 如果(P)问题((D)问题)有 最优解,那么(D)问题( (P)问题)也有最优解, 且目标函数值相等。 proof Corollary 4 (单纯形乘子定理) 如果(P)问题有最优解, 最优基为 B,则 w* = cBB-1 就是(D)问题的一个最优 解。 向前