
第10章 使用导数的最优化方法 本章和下一章研究无约束问题最优化方法.我们把无约束问 题的算法大致分成两类:其中之一,在计算过程中要用到目标函 数的导数,凡属这类算法在本章介绍;另一类只用到目标函数值, 不必计算导数,通常称为直接方法,放在第11章讨论. 一般来说,无约束问题的求解通过一系列一维搜索来实现因 此,怎样选择搜索方向是解无约束问题的核心问题,搜索方向的不 同选择,形成不同的最优化方法. §10.1最速下降法 10.1.1 最速下降方向 考虑无约束问题 min f(x)x∈R” (10.1.1)
第10章 使用导数的最优化方法 本章和下一章研究无约束问题最优化方法.我们把无约束问 题的算法大致分成两类:其中之一,在计算过程中要用到目标函 数的导数,凡属这类算法在本章介绍;另一类只用到目标函数值, 不必计算导数,通常称为直接方法,放在第11章讨论. 一般来说,无约束问题的求解通过一系列一维搜索来实现.因 此,怎样选择搜索方向是解无约束问题的核心问题,搜索方向的不 同选择,形成不同的最优化方法. §10.1 最速下降法 10.1.1 最速下降方向 考虑无约束问题 min ( ) n f x x R (10.1.1)

其中函数(x)具有一阶连续偏导数 人们在处理这类问题时,总希望从某一点出发,选择一个目标 函数值下降最快的方向,以利于尽快达到极小点.正是基于这样 种愿望,早在1847年法国著名数学家Cauchy提出了最速下降法 后来,Cury等人作了进一步的研究.现在最速下降法已经成为众 所周知的一种最基本的算法,它对其他算法的研究也很有启发作 用,因此在最优化方法中占有重要地位.下面我们先来讨论怎样选 择最速下降方向. 我们知道,函数(x)在点x处沿方向d的变化率可用方向 导数来表达,对于可微函数,方向导数等于梯度与方向的内积,即 Df(x;d)=Vf(x)'d (10.1.2) 因此,求函数f(x)在点x处的下降最快的方向,可归结为求解下 列非线性规划: min Vf(x)'d S.t ds1 (10.1.3)
其中函数 具有一阶连续偏导数. 人们在处理这类问题时,总希望从某一点出发,选择一个目标 函数值下降最快的方向,以利于尽快达到极小点.正是基于这样一 种愿望,早在1847年法国著名数学家Cauchy提出了最速下降法. 后来,Curry等人作了进一步的研究.现在最速下降法已经成为众 所周知的一种最基本的算法,它对其他算法的研究也很有启发作 用,因此在最优化方法中占有重要地位.下面我们先来讨论怎样选 择最速下降方向. 我们知道,函数 在点 处沿方向 的变化率可用方向 导数来表达,对于可微函数,方向导数等于梯度与方向的内积,即 f (x) f (x) x d Df x d f x d T ( ; ) = ( ) (10.1.2) 因此,求函数 在点 处的下降最快的方向,可归结为求解下 列非线性规划: f (x) x . 1 min ( ) st d f x d T (10.1.3)

根据Schwartz不等式,有 f(x)'d≤If(x)d≤f(x) 去掉绝对值符号,可以得到 Vf(x)'d≥-f(x) (10.1.4) 由上式可知,当 Vf(x) d=- IVf(x)川 (10.1.5) 时等号成立.因此,在点x处沿(10.1.5)所定义的方向变化率最小 即负梯度方向为最速下降方向 注:在不同尺度下最速下降方向是不同的前面定义的最速下 降方向,是在向量d的欧氏范数,不大于1的限制得到的,属于 欧氏度量意义下的最速下降方向如果改用其他度量
根据Schwartz不等式,有 f (x) d f (x) d f (x) T 去掉绝对值符号,可以得到 f (x) d f (x) T − (10.1.4) 由上式可知,当 ( ) ( ) f x f x d = − (10.1.5) 时等号成立.因此,在点 处沿(10.1.5)所定义的方向变化率最小, 即负梯度方向为最速下降方向. 注:在不同尺度下最速下降方向是不同的.前面定义的最速下 降方向,是在向量 的欧氏范数 不大于1的限制得到的,属于 欧氏度量意义下的最速下降方向.如果改用其他度量, x d 2 d

如,设A为对称正定矩阵,在向量d的A范数d,=(d”Ad)2不大 于1的限制下,极小化Vf(x)d,则得到的最速下降方向与前者 不同. 10.1.2最速下降算法 最速下降法的迭代公式是 x(k+1)=x(k)tad(k) (10.1.6) 其中dk是从x(k出发的搜索方向,这里取在点x(k)处的最速下 降方向,即 d)=-7f(xk) 2,是从x)出发沿方向d)进行一维搜索的步长,即人满足 f(xd()=min f(x+d() (10.1.11)
如,设 为对称正定矩阵,在向量 的 范数 不大 于1的限制下,极小化 ,则得到的最速下降方向与前者 不同. A d A 2 1 d (d Ad) T A = f x d T ( ) 10.1.2 最速下降算法 最速下降法的迭代公式是 ( 1) ( ) (k ) k k k x = x + d + (10.1.6) 其中 是从 出发的搜索方向,这里取在点 处的最速下 降方向,即 ( ) (k ) (k ) d = −f x (k ) d (k ) x k 是从 x (k ) 出发沿方向 d (k ) 进行一维搜索的步长,即 k 满足 ( ) min ( ) ( ) ( ) 0 ( ) (k ) k k k k f x d f x d + = + (10.1.11) (k ) x

计算步骤如下: 1.给定初点x①∈R”,允许误差δ>0,置k=1. 2.计算搜索方向d)=-☑f(x) 3.若d≤6,则停止计算;否则,从x出发,沿d)进行 一维搜索,求”,使 (d)=min f()d) 4.令xk+)=xk)+九d),置k=k+1,转步2. 例10.1.1 用最速下降法解下列问题: min f(x)=2x+x 初点x"=(1,1)',6=1 0
计算步骤如下: 1.给定初点 ,允许误差 ,置 . (1) n x R 0 k =1 2.计算搜索方向 ( ) (k ) (k ) d = −f x 3.若 ,则停止计算;否则,从 出发,沿 进行 一维搜索,求 ,使 (k ) d (k ) x (k ) d k ( ) min ( ) ( ) ( ) 0 ( ) (k ) k k k k f x d f x d + = + 4.令 ,置 ,转步2.. ( 1) ( ) (k ) k k k x = x + d + k := k +1 例10.1.1 用最速下降法解下列问题: 2 2 2 1 min f (x) = 2x + x . 10 1 (1,1) , (1) = = T 初点x

例10.1.1用最速下降法求非线性规划问题 min f(X)=x2+25x, 取初始点X0=(2,2),允许误差ε=10-6。 解:f(X0)=104,Vf(x)=(2x1,50x2), Vf(X0)=(4,100) )fX0=V42+1002=10016 由 2Xo0+d)=0得元,=0.02003。 故 X0=Xo-27f(Xo)=(1.92,-0.003) f(X0)=3.69
例10.1.1 用最速下降法求非线性规划问题 (0) ( ) (4,100)T = f X 1 2 ( ) (2 ,50 ) , T = f x x x (0) f X( ) 104, = 6 10− X (0) = (2,2) , T = 。 2 2 min ( ) 25 1 2 f X x x = + 取初始点 允许误差 解: 0 2 2 = + = f X 4 100 10016 ( ( ) ) (1) f X( ) 3.69 = (1) (0) (0) 0 ( ) (1.92, 0.003)T X X f X = − = − d f X d ( ) 0 (0) (0) 故 d 由 + = 得 0 = 0.02003

前三次迭代过程如表1。 表1 迭代 次数 点 X X2 f(X() f(x) 0 YO) 0.02003 2 2 (4,100)7 104 1 X四 0.4824 1.92 -0.003 (3.84,-0.15) 3.69 X(2) 2 0.020 0.07 0.070 (0.14,3.50) 0.13 P(3) 3 0.07 -0.000 经过10轮迭代,即可满足允许误差£=10-6的 要求,迭代过程的几何表示如图10.1.1
前三次迭代过程如表1。 表1 迭代 次数 点 0 0.02003 2 2 104 1 0.4824 1.92 -0.003 3.69 2 0.020 0.07 0.070 0.13 3 —— 0.07 -0.000 —— —— 6 10− = (0.14,3.50)T (3.84, 0.15)T − 4,100) ( T (3) X (2) X (1) X 0 X ( ) ( ) ( ) k f X ( ) ( ) k k x1 x2 f X 经过10轮迭代,即可满足允许误差 的 要求, 迭代过程的几何表示如图10.1.1
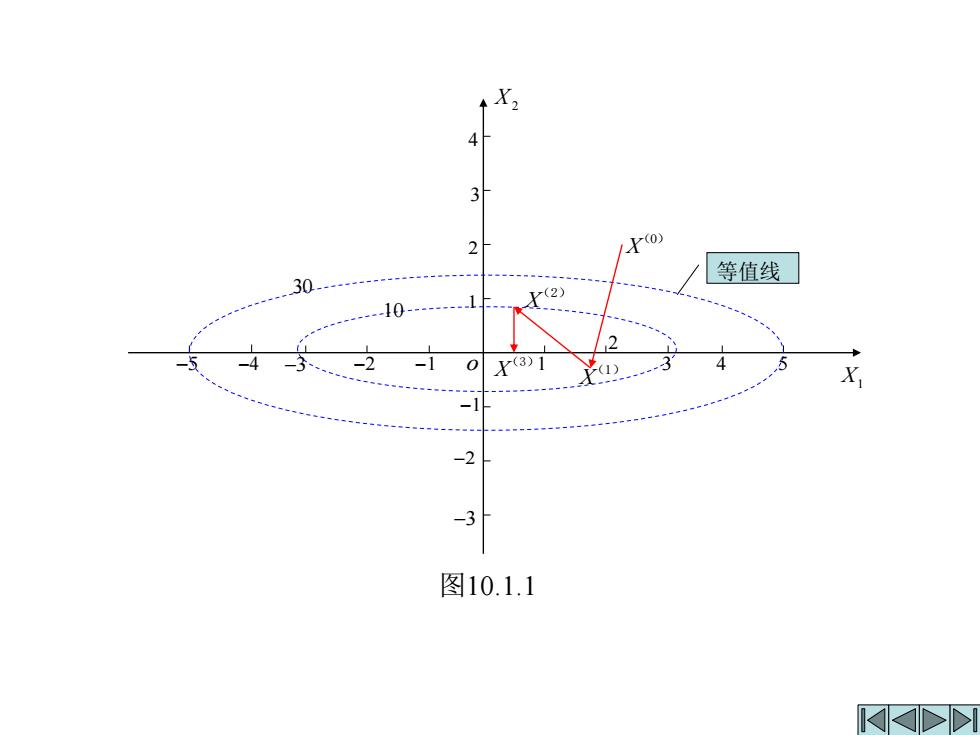
4 3 2 等值线 30 - -(2) 10 2 -4 -3 -1 0 X3)1 4 5 X -2 -3 图10.1.1
0 X ( ) X1 1 X (3) X (2) X −5 −4 1 (1) −3 −2 −1 4 3 2 −3 −2 −1 3 4 5 2 X2 o 10 30 等值线 图10.1.1

由图10.1.1可知,Xk随着迭代次数的增加,越 来越接近于最优解(0,0)严,但是我们也应该注意到 一个问题,随着迭代次数的增加,收敛速度越来越 慢,在极小点附近,X逼近最优解的路径呈锯齿 形,这种现象称为“锯齿现象这种算法的依据仍 然是梯度。梯度是用来刻画函数的局部性质的,在 某一点的邻域内函数值下降最快,但从求解极小点 的全部过程来看并不一定最快。 虽然最速下降法收敛速度较慢,但它却因方法 简便,计算量和存贮量少而被人们广泛使用,在实 际运用时,常将最速下降法和其它方法结合使用。 在前期使用最速下降法,而在接近极小点时则改用 其它收敛较快的方法
由图10.1.1可知, 随着迭代次数的增加, (0,0 , )T ( ) k X 越 来越接近于最优解 但是我们也应该注意到 一个问题,随着迭代次数的增加,收敛速度越来越 慢,在极小点附近, ( ) k X 逼近最优解的路径呈锯齿 形,这种现象称为“锯齿现象”。这种算法的依据仍 然是梯度。梯度是用来刻画函数的局部性质的,在 某一点的邻域内函数值下降最快, 的全部过程来看并不一定最快。 但从求解极小点 虽然最速下降法收敛速度较慢,但它却因方法 简便,计算量和存贮量少而被人们广泛使用,在实 际运用时,常将最速下降法和其它方法结合使用。 在前期使用最速下降法,而在接近极小点时则改用 其它收敛较快的方法

§10.2 牛顿法 10.2.1 牛顿法 设f(x)是二次可微实函数,x∈R”.又设xk)是f(x)的极小点 的一个估计,我们把f(x在xk)展成Taylor级数,并取二阶近似: f(x)≈(x) f(x()+Vf(x()"(x-x)) +(-xyVf(x"Xx-x) 其中V2f(x)是f(x)在xk)处的Hesse矩阵.为求x)的平稳 点,令 V(x)=0 即 Vf(x()+v2f(x)(x-x)=0 (10.2.1)
§10.2 牛顿法 10.2.1 牛顿法 设 是二次可微实函数, .又设 是 的极小点 的一个估计,我们把 在 展成Taylor级数,并取二阶近似: f (x) n x R (k ) x f (x) f (x) (k ) x ( ) ( )( ) 2 1 ( ) ( ) ( ) ( ) ( ) ( ) 2 ( ) ( ) ( ) ( ) ( ) k T k k k k T k x x f x x x f x f x x x f x x + − − = + − 其中 是 在 处的Hesse矩阵. 为求 的平稳 点,令 ( ) 2 (k ) f x f (x) (k ) x (x) (x) = 0 ( ) ( )( ) 0 ( ) 2 ( ) ( ) + − = k k k 即 f x f x x x (10.2.1)