
特征值与特征向量 张莉 Email:lizhang@tongji.edu.cn 可济大争数学系 June5,2015 4907 聘同济大单 Jue320151/35
. . 特征值与特征向量 张 莉 Email:lizhang@tongji.edu.cn 同济大学 数学系 June 5, 2015 ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 1 / 35

§1.1.向量的内积与长度 X1 1.定义1.P.111)设x= 和y= 是两个n维列向量,则定义它们的内 积为: [x,y=xy1+…+xyn 2.说明 ().内积是向量的一种运算,如果x,y都是列向量,内积可用矩阵记号表示:x,习=xy 3.例:用内积的话言重速矩车通法的定义 ,内积的若干话程性所P1) ..y=对称生 ,入=入 面以十因=三十因 w,正定件当x=0时,,=当1≠0叫,>0 聘同济大举 Jue320152/36
§1.1. 向量的内积与长度 1. 定义 1.(P.111) 设 x = x1 . . . xn 和 y = y1 . . . yn 是两个 n 维列向量, 则定义它们的内 积为: [x, y] = x1y1 + · · · + xnyn 2. 说明 (1). 内积是向量的一种运算, 如果 x, y 都是列向量,内积可用矩阵记号表示:[x, y] = x T y 3. 例: 用内积的语言重述矩阵乘法的定义. 4. 内积的若干运算性质 (P.111) (i). [x, y] = [y, x] (对称性) (ii). [λx, y] = λ[x, y] (iii). [x + y,z] = [x,z] + [y,z]; (iv). 正定性: 当 x = 0 时, [x, x] = 0; 当 x ̸= 0 时, [x, x] > 0. ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 2 / 35

§1.1.向量的内积与长度 X1 1 1.定义1.P.111)设x= 和y= 是两个n维列向量,则定义它们的内 y。 积为: [x,y=xy1十…+xyn 2.说明 ().内积是向量的一种运算,如果x,y都是列向量,内积可用矩阵记号表示:x,习=xy 3.例:用内积的语言重述矩阵乘法的定义 ,内积的若干西是件成P ..=对称性 ,入=入 面以十因=三十因 w,正定件当x=0时,,=当1≠0叫,>0 聘同济大举 Je320152/36
§1.1. 向量的内积与长度 1. 定义 1.(P.111) 设 x = x1 . . . xn 和 y = y1 . . . yn 是两个 n 维列向量, 则定义它们的内 积为: [x, y] = x1y1 + · · · + xnyn 2. 说明 (1). 内积是向量的一种运算, 如果 x, y 都是列向量,内积可用矩阵记号表示:[x, y] = x T y 3. 例: 用内积的语言重述矩阵乘法的定义. 4. 内积的若干运算性质 (P.111) (i). [x, y] = [y, x] (对称性) (ii). [λx, y] = λ[x, y] (iii). [x + y,z] = [x,z] + [y,z]; (iv). 正定性: 当 x = 0 时, [x, x] = 0; 当 x ̸= 0 时, [x, x] > 0. ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 2 / 35

§1.1.向量的内积与长度 X1 1.定义1.P.111)设x= 和y= 是两个n维列向量,则定义它们的内 y 积为: [x,y=xy1十…+xyn 2.说明 ().内积是向量的一种运算,如果x,y都是列向量,内积可用矩阵记号表示:x,习=xy 3.例:用内积的语言重述矩阵乘法的定义 4.内积的若干千运算性质(P.111) .x,习=,(对称性) m.[x,习=, (m).r+,司=,司+y,小 w.正定性:当x=0时,x,=0:当x≠0时,[x,>0 聘同济大举 Jue520152/35
§1.1. 向量的内积与长度 1. 定义 1.(P.111) 设 x = x1 . . . xn 和 y = y1 . . . yn 是两个 n 维列向量, 则定义它们的内 积为: [x, y] = x1y1 + · · · + xnyn 2. 说明 (1). 内积是向量的一种运算, 如果 x, y 都是列向量,内积可用矩阵记号表示:[x, y] = x T y 3. 例: 用内积的语言重述矩阵乘法的定义. 4. 内积的若干运算性质 (P.111) (i). [x, y] = [y, x] (对称性) (ii). [λx, y] = λ[x, y] (iii). [x + y,z] = [x,z] + [y,z]; (iv). 正定性: 当 x = 0 时, [x, x] = 0; 当 x ̸= 0 时, [x, x] > 0. ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 2 / 35
5.定义2(P.112): 令l=V低,可=√好+…+x 称xl为n维向量x的长度(或范数): .向量的度其有还性班 1非候件.之0且用=0仅当x零向量明 2行次住订=A 3三布x+≤+1 .当=1称x为单0国 端同济大举 Ju20153/35
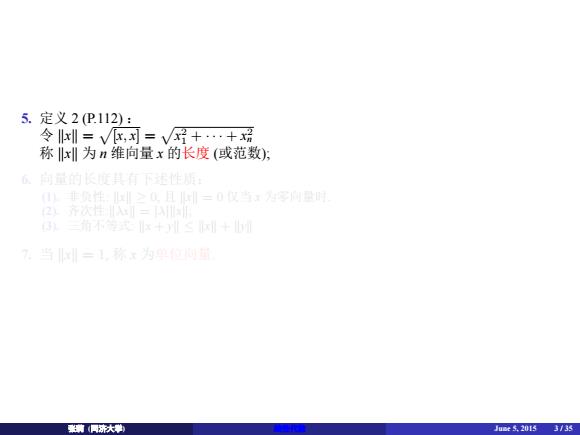
5. 定义 2 (P.112) : 令 ∥x∥ = √ [x, x] = √ x 2 1 + · · · + x 2 n 称 ∥x∥ 为 n 维向量 x 的长度 (或范数); 6. 向量的长度具有下述性质: (1). 非负性: ∥x∥ ≥ 0, 且 ∥x∥ = 0 仅当 x 为零向量时. (2). 齐次性:∥λx∥ = |λ|∥x∥; (3). 三角不等式: ∥x + y∥ ≤ ∥x∥ + ∥y∥ 7. 当 ∥x∥ = 1, 称 x 为单位向量. ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 3 / 35

5.定义2(P112): 令l=V低,可=√好+…+x 称xl为n维向量x的长度(或范数): 6.向量的长度具有下述性质: (1).非负性:x≥0,且x=0仅当x为零向量时 (2,.齐次性:入xl=lx: (③).三角不等式:x+≤xl+lby .当=1称x为独 端同济大举 Ju20153/35
5. 定义 2 (P.112) : 令 ∥x∥ = √ [x, x] = √ x 2 1 + · · · + x 2 n 称 ∥x∥ 为 n 维向量 x 的长度 (或范数); 6. 向量的长度具有下述性质: (1). 非负性: ∥x∥ ≥ 0, 且 ∥x∥ = 0 仅当 x 为零向量时. (2). 齐次性:∥λx∥ = |λ|∥x∥; (3). 三角不等式: ∥x + y∥ ≤ ∥x∥ + ∥y∥ 7. 当 ∥x∥ = 1, 称 x 为单位向量. ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 3 / 35

5.定义2(P112) 令l=V低,可=√好+…+x 称xl为n维向量x的长度(或范数): 6.向量的长度具有下述性质: (1).非负性:x≥0,且x=0仅当x为零向量时. (2,.齐次性:入xl=lx: (③).三角不等式:x+≤xl+lby 7.当xl=1,称x为单位向量 端同济大举 Ju52053/35
5. 定义 2 (P.112) : 令 ∥x∥ = √ [x, x] = √ x 2 1 + · · · + x 2 n 称 ∥x∥ 为 n 维向量 x 的长度 (或范数); 6. 向量的长度具有下述性质: (1). 非负性: ∥x∥ ≥ 0, 且 ∥x∥ = 0 仅当 x 为零向量时. (2). 齐次性:∥λx∥ = |λ|∥x∥; (3). 三角不等式: ∥x + y∥ ≤ ∥x∥ + ∥y∥ 7. 当 ∥x∥ = 1, 称 x 为单位向量. ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 3 / 35

正交向量组 1.定义1:称两向量x和y正交,若其内积x,=0. 工定义2:正向品组一一组两西正交的非零向量档成的向量细 3.定理1化2任一正向量组,·必线性无关 城正 聘同济大举 Jue520154/35
正交向量组 1. 定义 1.: 称两向量 x 和 y 正交, 若其内积 [x, y] = 0. 2. 定义 2.: 正交向量组 — 一组两两正交的非零向量构成的向量组. 3. 定理 1 (P.112) 任一正交向量组 {a1, · · · , ar} 必线性无关. 䇷: (用线性无关定义来证) 若有数 λ1, · · · , λr 使得 λ1a1 + · · · + λrar = 0 两边与 ai 作内积, 用分配律与正交性条件得 λi[ai, ai] = 0, 再由 ai 非零得 λi = 0. 故 λ1 = · · · = λr = 0. 即向量组 {a1, · · · , ar} 线性无关. 4. 定义 3(P.113) 规范正交组 — 由单位向量们组成的正交向量组. 5. 例:R 3 中, 单位坐标向量组 e1 = 1 0 0 , e2 = 0 1 0 , e3 = 0 0 1 为规范正交组. e ′ 1 = cos θ sin θ 0 , e ′ 2 = − sin θ cos θ 0 , e ′ 3 = 0 0 1 ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 4 / 35

正交向量组 L.定义1:称两向量x和y正交,若其内积x,川=0 2.定义2:正交向量组一一组两两正交的非零向量构成的向量组 3.定理1化2)任一正向量纽::,}必线性无关 正(用钱件无关定义来证)着有数,一,入使得 山1十+人,=0 两过与作内积用分配单与正交性条得入@,三0再由心非家宿入=0 入===0.即向量组{.,,或住无大 三中中的 聘同济大举 Jue520154/35
正交向量组 1. 定义 1.: 称两向量 x 和 y 正交, 若其内积 [x, y] = 0. 2. 定义 2.: 正交向量组 — 一组两两正交的非零向量构成的向量组. 3. 定理 1 (P.112) 任一正交向量组 {a1, · · · , ar} 必线性无关. 䇷: (用线性无关定义来证) 若有数 λ1, · · · , λr 使得 λ1a1 + · · · + λrar = 0 两边与 ai 作内积, 用分配律与正交性条件得 λi[ai, ai] = 0, 再由 ai 非零得 λi = 0. 故 λ1 = · · · = λr = 0. 即向量组 {a1, · · · , ar} 线性无关. 4. 定义 3(P.113) 规范正交组 — 由单位向量们组成的正交向量组. 5. 例:R 3 中, 单位坐标向量组 e1 = 1 0 0 , e2 = 0 1 0 , e3 = 0 0 1 为规范正交组. e ′ 1 = cos θ sin θ 0 , e ′ 2 = − sin θ cos θ 0 , e ′ 3 = 0 0 1 ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 4 / 35

正交向量组 L.定义1:称两向量x和y正交,若其内积x,=0 2.定义2:正交向量组一一组两两正交的非零向量构成的向量组 3.定理1(P.112)任一正交向量组{a1,…,a}必线性无关 正用钱性无关定义来证着有数,一一,入,使福 1十+人,,=0 两过与作内积用分配单与正交性条得入@,三0再由心非家宿入=0 放入===0即向量组创:·,4山,线住无 4.定义3P113)号用一由单位向量用成的正里红 聘同济大举 Je520154/35
正交向量组 1. 定义 1.: 称两向量 x 和 y 正交, 若其内积 [x, y] = 0. 2. 定义 2.: 正交向量组 — 一组两两正交的非零向量构成的向量组. 3. 定理 1 (P.112) 任一正交向量组 {a1, · · · , ar} 必线性无关. 䇷: (用线性无关定义来证) 若有数 λ1, · · · , λr 使得 λ1a1 + · · · + λrar = 0 两边与 ai 作内积, 用分配律与正交性条件得 λi[ai, ai] = 0, 再由 ai 非零得 λi = 0. 故 λ1 = · · · = λr = 0. 即向量组 {a1, · · · , ar} 线性无关. 4. 定义 3(P.113) 规范正交组 — 由单位向量们组成的正交向量组. 5. 例:R 3 中, 单位坐标向量组 e1 = 1 0 0 , e2 = 0 1 0 , e3 = 0 0 1 为规范正交组. e ′ 1 = cos θ sin θ 0 , e ′ 2 = − sin θ cos θ 0 , e ′ 3 = 0 0 1 ᕖ㦿 (同⎄ཝᆜ) 线性代ᮦ June 5, 2015 4 / 35