
§3荔数的极限 第一章 在上一节我们学习数列的极限 数列{x,}可看作自变量 为n的函数:xnn),n∈N+,所以,数列{xn}的极限为a,就是 当自变量n取正整数而无限增大(即no)时,对应的函数值 fn)无限接近于某个确定的数a/把数列极限概念中的函数 为(n而自变量的变化过程为n→oo等特殊性撇开,就可以 引出函数极限的一般概念。 在自变量的某一变化过程中,如果对应的函数值无限 接近于某个确定的数,那未这个确定的数就叫做在这一变 化过程中函数的极限。这个极限是与自变量的变化过程密 切相关的,由于自变量的变化过程不同,函数的极限也就 表现为不同的形式。 动 结球
第一章 机动 目录 上页 下页 返回 结束 §3 函数的极限 在上一节我们学习数列的极限,数列{xn}可看作自变量 为n的函数:xn =f(n),n∈N+ ,所以,数列{xn}的极限为a,就是 当自变量n取正整数而无限增大(即n→∞)时,对应的函数值 f(n)无限接近于某个确定的数a,把数列极限概念中的函数 为f(n)而自变量的变化过程为n→∞等特殊性撇开,就可以 引出函数极限的一般概念。 在自变量的某一变化过程中,如果对应的函数值无限 接近于某个确定的数,那末这个确定的数就叫做在这一变 化过程中函数的极限。这个极限是与自变量的变化过程密 切相关的,由于自变量的变化过程不同,函数的极限也就 表现为不同的形式

数列的极限看作函数n)当n→oo时的极限,这里的自 变量的变化过程是o.而函数极限的自变量的变化为 对y=f(x),自变量变化过程的六种形式 (1)x→x0 (4)x>0 (2)x→x0 (5)x→+ (3 x→x0 (6 X→-00 本节内容: 自变量趋于有限值时函数的极限 二、 自变量趋于无穷大时函数的极限 HIGH EDUCATION PRESS 机动目录上页下页返回结束
一、自变量趋于有限值时函数的极限 自变量变化过程的六种形式: 二、自变量趋于无穷大时函数的极限 本节内容 : 机动 目录 上页 下页 返回 结束 数列的极限看作函数f(n) 当n→∞时的极限,这里的自 变量的变化过程是n→∞.而函数极限的自变量的变化为:

一、自变量趋于有限值时函数的极限 1.x→x,时函数极限的定义 引例.测量正方形面积(真值:边长为xo;面积为A) 直接观测值 确定直接观测值精度δ: 边长x |x-xo<δ 间接观测值 任给精腹6,要求x2-A<ε 面积x2 机动目 上页下页返回结束
一、自变量趋于有限值时函数的极限 1. 时函数极限的定义 引例. 测量正方形面积. (真值: 边长为 面积为A ) 边长 面积 直接观测值 间接观测值 任给精度 , 要求 x − A 2 确定直接观测值精度 : x − x0 0 A x 机动 目录 上页 下页 返回 结束

定义1,设函数f(x)在点x的某去心邻域内有定义, 若Ve>0,3δ>0,当00,38>0,当x∈U(xo,6) x→X0 时,有f(x)-A<8 几何解释: A+8 y元f(x) 这表明: A 极限存在 A-8 函数局部有界 xo-δXox0+6x 机动目影 上页下页返回结束
定义1 . 设函数 在点 的某去心邻域内有定义 , 0, 0, 当 0 x − x0 时, 有 f (x) − A 则称常数 A 为函数 当 时的极限, f x A x x = → lim ( ) 0 或 即 当 时, 有 若 记作 几何解释: x0 + A+ A− A x0 x y y = f (x) 极限存在 函数局部有界 这表明: 机动 目录 上页 下页 返回 结束

例1.证明limC=C(C为常数) x→x0 证: |f(x)-A=C-C=0 故Ve>0,对任意的δ>0,当0<x-x<6时, 总有 C-C=0<6 因此 lim C=C x-今x0 机动目录上页下页返回结束
例1. 证明 证: f (x) − A 故 0, 对任意的 0, 当 时 , 因此 总有 机动 目录 上页 下页 返回 结束

例2.证明1im(2x-1)=1 x>1 证:f(x)-A=(2x-1)-1=2x-1 8>0,欲使/)-4<,尺要x-l<号 取6=,则当0<x-1<6时,必有 2 f(x)-A=(2x-1)-1<8 因此1im(2x-1)=1 OC8 机动目录上页下页返回结束
例2. 证明 证: = 2 x −1 0, 欲使 取 , 2 = 则当 0 x −1 时 , 必有 因此 只要 机动 目录 上页 下页 返回 结束

例3.证明1im 2-1 =2 x>1x-1 证/)-A= 故V6>0,取δ=6,当0<x-1<8时,必有 x2-1-2<8 x-1 因此lim -1=2 x1x-1 机动目录上页下页返回结束
例3. 证明 证: f (x) − A 故 0, 取 = , 当 时 , 必有 − − − 2 1 1 2 x x 因此 2 1 1 lim 2. x 1 x → x − = − 机动 目录 上页 下页 返回 结束

爸等数兴 第九讲 区数的极根 主讲教师:陈殿友 总课时:124
主讲教师:陈殿友 总课时:124 第九讲 函数的极限

2.保号性定理 定理1.若1imf(x)=A,且A>0,则存在U(xo,6), x今X0 (A≤0) 使当x∈U(x,δ)时,f(x)>0 (f(x)0,3U(xo,8),当 x→x0 x∈U(xo,6)时,有A-80时,取正数6≤A, ↑y A+ yラf(x) (≤0) (8≤-A) 则在对应的邻域U(xo,6)上 A-8 f(x)>0 x,-6X0x0+δx (<0) 机动目录 上页下页返回结束
2. 保号性定理 定理1 . 若 且 A > 0 , f (x) 0. ( f (x) 0) 证: 已知 即 0, 当 时, 有 当 A > 0 时, 取正数 则在对应的邻域 上 (< 0) ( −A) 则存在 ( A < 0 ) ( 0) 机动 目录 上页 下页 返回 结束
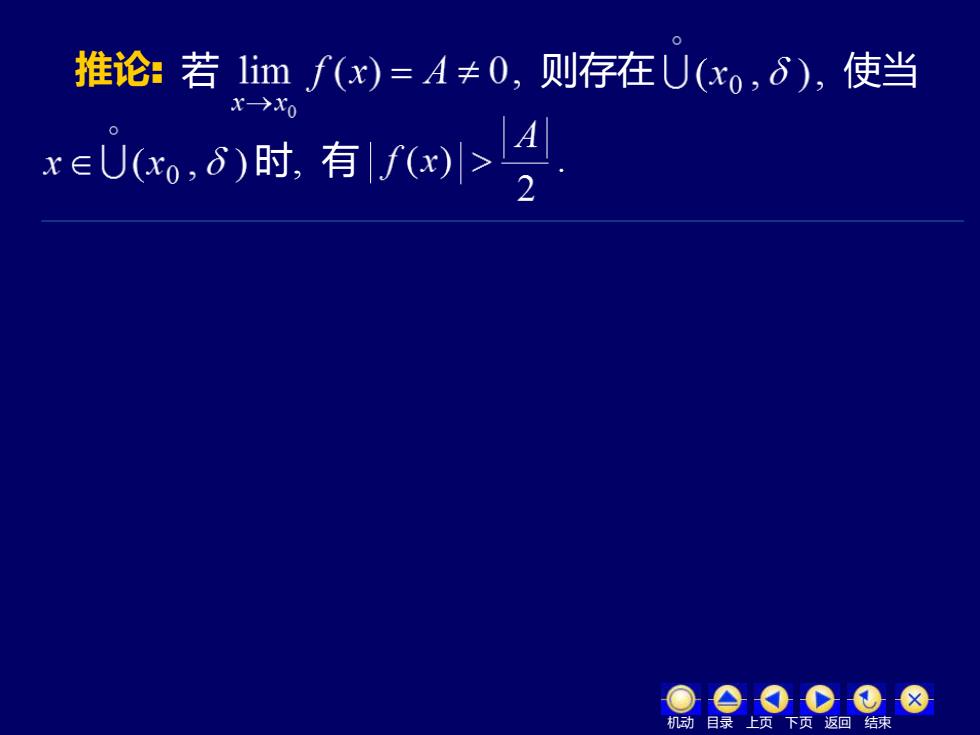
推论:若1imf(x)=A≠0,则存在U(xo,δ),使当 eU时有/s号 机动目录上页下页返回结束
若 则存在 使当 时, 有 推论: 机动 目录 上页 下页 返回 结束