
第一—章 §8盈教的连疾性与间断点 函数连续性的定义 二、 函数的间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、 函数的间断点 一、 函数连续性的定义 机动 目录 上页 下页 返回 结束 §8函数的连续性与间断点 第一章

函数连续性的定义 自然界有许多现象,如气温的变化,江河的水流,植 物的生长等等,都是连续地变化着的这种现象反映在函 数上,就是函数的连续性.例如就气温的变化来看,当时 间变动很微小时,气温的变化也很微小,这种特点就是 所谓的连续性 为了更好的刻画连续性,我们先引出增量的概念 设变量从它的一个初值u变到终值u2,终值与初值的 差u1~2就叫做变量的增量,记作△4,即 △u=142-41 1、增量△可以是正的,也可以是负的 2、记号△讲不表示某个量△与变量的乘积,而是一 个整体不可分割的记号 HIGH EDUCATION PRESS 00 机动目录上页下页 返[ 结
一、 函数连续性的定义 机动 目录 上页 下页 返回 结束 自然界有许多现象,如气温的变化,江河的水流,植 物的生长等等,都是连续地变化着的.这种现象反映在函 数上,就是函数的连续性.例如就气温的变化来看,当时 间变动很微小时,气温的变化也很微小,这种特点就是 所谓的连续性. 为了更好的刻画连续性,我们先引出增量的概念. 设变量u从它的一个初值u1变到终值u2,终值与初值的 差u1 - u2就叫做变量u的增量,记作 u, 即 2 1 = − u u u . 2、记号 1、增量 u 可以是正的,也可以是负的. u 并不表示某个量△与变量u的乘积,而是一 个整体不可分割的记号

定义1设函数y=f(x)在x的某邻域内有定义 如果limf(x)存在,且l1imf(x)=f(xo), 则称函数 X-X0 f(x)在x连续 可见,函数f(x)在点x,连续必须具备下列条件 (I)f(x)在点xo有定义,即f(xo)存在; (2) 极限limf(x)存在; x→x0 3 lim f(x)=f(xo). x→x0 连续函数的图形是一条连续而不间断的曲线 HIGH EDUCATION PRESS 机动目录上页下页返回结束
可见 , 函数 在点 0 x 定义1 在 的某邻域内有定义 , 则称函数 ( ) . f x 在x0 连续 (1) 在点 即 (2) 极限 (3) 设函数 连续必须具备下列条件: 存在 ; 且 有定义 , 存在 ; 机动 目录 上页 下页 返回 结束 如果 0 lim ( ) x x f x → 存在, (4) 连续函数的图形是一条连续而不间断的曲线

若f(x)在某区间上每一点都连续,则称它在该区间上 连续,或称它为该区间上的连续函数 在闭区间[a,b]上的连续函数的集合记作C[a,b] 例如,P(x)=ao+a41x+…+anx” 有理整函数) 在(-0,十0)上连续 又如,有理分式函数R(x)= P(x) Q(x) 在其定义域内连续 只要Q(xo)≠0,都有1imR(x)=R(xo) x→x0 HIGH EDUCATION PRESS 机动目录上页下页返回结束
( , ), lim ( ) ( ) continue 0 0 0 x P x P x x x − + = → 若 在某区间上每一点都连续 , 则称它在该区间上 连续 , 或称它为该区间上的连续函数 . C[a, b]. 例如, 在 上连续 . ( 有理整函数 ) 又如, 有理分式函数 在其定义域内连续. 在闭区间 上的连续函数的集合记作 只要 ( ) 0, Q x0 都有 lim ( ) ( ) 0 0 R x R x x x = → 机动 目录 上页 下页 返回 结束

对自变量的增量△x=x-x0,有函数的增量 △y=f(x)-f(xo)=f(x0+△x)-f(xo) 函数f(x)在点x,连续有下列等价命题 lim f(x)=f(xo) limf(xo+△x)=f(xo) x-→X0 Ax->0 lim△y=0 yy=f(x △x-→0 f(xo )f(xo)=f(xo") △x 左连续 右连续 Xx Vε>0,38>0,当x-=Ax<8时,有 f(x)-f(x=△yKe HIGH EDUCATION PRESS 机动目录上页下页返回结束
对自变量的增量 有函数的增量 y = f (x) o x y 0 x x x y lim ( ) ( ) 0 0 f x f x x x = → lim ( ) ( ) 0 0 0 f x x f x x + = → lim 0 0 = → y x ( ) ( ) ( ) 0 0 0 − + f x = f x = f x 左连续 右连续 0, 0, 当 x − x0 = x 时, 有 f (x) − f (x ) = y 0 函数 在点 连续有下列等价命题: 机动 目录 上页 下页 返回 结束

例.证明函数y=sinx在(-o,+oo)内连续 证:x∈(-0,+∞) Ay=sin(x+Ax)-sinx =2sin cos(x+) Ay=2 sin cos(x+) ≤21=AxAx→0 即 lim.△y=0 △x→0 这说明y=sinx在(-o,+oo)内连续 同样可证:函数y=C0Sx在(-0,十0)内连续 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例. 证明函数 在 内连续 . 证: x(−, + ) y = sin(x + x) −sin x 2 sin cos( ) 2 2 x x y x = + = x x → 0 即 这说明 在 内连续 . 同样可证: 函数 在 内连续 . 0 机动 目录 上页 下页 返回 结束

二、 函数的间断点 设f(x)在点x,的某去心邻域内有定义,则下列情形 之一函数f(x)在点x,不连续 (1)函数f(x)在x,无定义; (2)函数f(x)在x,虽有定义,但1mf(x)不存在 x→X0 (3)函数f(x)在x,虽有定义,且1mf(x)存在,但 x今X0 limf(x)≠f(xo) x→X0 这样的点x。称为间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束
在 在 二、 函数的间断点 (1) 函数 (2) 函数 不存在; (3) 函数 存在 , 但 lim ( ) ( ) 0 0 f x f x x x → 不连续 : 设 在点 的某去心邻域内有定义 , 则下列情形 这样的点 之一函数 f (x) 在点 虽有定义 , 但 虽有定义 , 且 称为间断点 . 在 无定义 ; 机动 目录 上页 下页 返回 结束

间断点分类: 第一类间断点: f(x。)及f(x,)均存在 若f(x,)=f(x,),称xo为可去间断点 若f(x,)≠f(x,),称x,为跳跃间断点 第二类间断点: f(x。)及f(x,)中至少一个不存在 若其中有一个为0,称x,为无穷间断点 若其中有一个为振荡,称x。为振荡间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束
间断点分类: 第一类间断点: 及 均存在 , 若 称 0 x 若 称 0 x 第二类间断点: 及 中至少一个不存在 , 称 0 x 若其中有一个为振荡 , 称 0 x 若其中有一个为 , 为可去间断点 . 为跳跃间断点 . 为无穷间断点 . 为振荡间断点 . 机动 目录 上页 下页 返回 结束
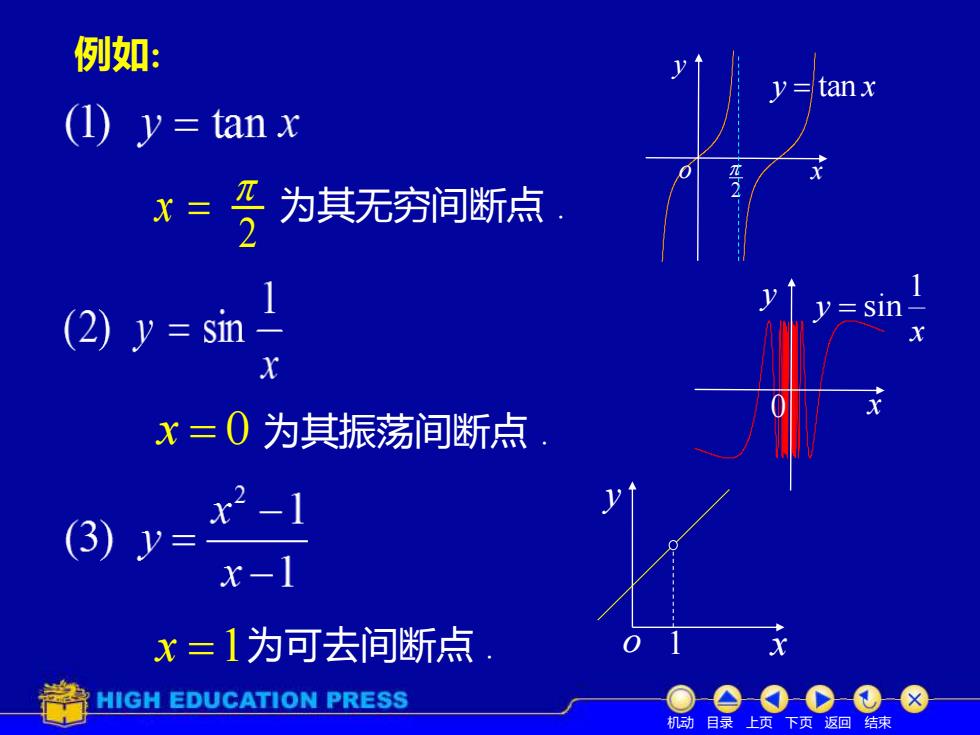
例如: =tanx (1)y=tanx x= 为其无穷间断点 1 (2)y sin 1y三 X x=0为其振荡间断点 x2-1 (3)y= x-1 x=1为可去间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束
2 x = 为其无穷间断点 . x = 0 为其振荡间断点 . x =1为可去间断点 . o x y 1 例如: y = tan x 2 x y o x y x y 1 = sin 0 机动 目录 上页 下页 返回 结束

x,x≠1 4y=={5,x=1 显然1imf(x)=1≠f() 112 x>1 X x=1为其可去间断点 x-1,x0 X f(0)=-1, f(0)=1 x=0为其跳跃间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束
1 lim ( ) 1 (1) 1 f x f x = → 显然 x =1 为其可去间断点 . = = = , 1 , 1 ( ) 2 1 x x x (4) y f x o x y 2 1 1 (5) + = − = = 1 , 0 0 , 0 1 , 0 ( ) x x x x x y f x x y o 1 −1 (0 ) = −1, − f (0 ) =1 + f x = 0 为其跳跃间断点 . 机动 目录 上页 下页 返回 结束