
第四章随机变量的数字特征 随机变量的概率分布反映了随机变量的统计规律性, 但是在实际问题中,要确定一个随机变量的分布不是一件 容易的事情.在许多情况下,并不需要求出随机变量的分 布,只须知道从不同角度反映随机变量取值特征的若干个 数字就够了,这些数字就称为随机变量的数字特征 本章将讨论随机变量的数学期望、方差、矩以及相关 系数,它们在概率论与数理统计中起着重要的作用. 第一节数学期望 一、离散型随机变量的数学期望 例1一台机床加工某种零件,已知它加工出优质品、合格品和废品的概 率依次为02、07和0.1.如果出售优质品和合格品,每一个零件可分别获利 0.40元和0.20元;如果加工出一件废品则要损失0.10元.问这台机床每加工出 一个零件,平均可获利多少元? 解以X表示加工出一个零件所获得的利润,则X的分布律为
第四章 随机变量的数字特征 随机变量的概率分布反映了随机变量的统计规律性, 但是在实际问题中,要确定一个随机变量的分布不是一件 容易的事情.在许多情况下,并不需要求出随机变量的分 布,只须知道从不同角度反映随机变量取值特征的若干个 数字就够了,这些数字就称为随机变量的数字特征. 本章将讨论随机变量的数学期望、方差、矩以及相关 系数,它们在概率论与数理统计中起着重要的作用. 第一节 数学期望 一、离散型随机变量的数学期望 例1 一台机床加工某种零件,已知它加工出优质品、合格品和废品的概 率依次为0.2、0.7和0.1.如果出售优质品和合格品,每一个零件可分别获利 0.40元和0.20元;如果加工出一件废品则要损失0.10元.问这台机床每加工出 一个零件,平均可获利多少元? 解 以 X 表示加工出一个零件所获得的利润,则X 的分布律为

-0.10 0.20 0.40 0.1 0.7 0.2 现假设该机床加工n个零件,其中废品n件,合格品n2件,优质品n3 件,这里n1+n2+n3=n.则这n个零件可以获得总利润为 -0.1n1+0.2n2+0.4n3, 平均每个零件可获利为 -0.1.2+0.2.2+0.4.乃. 之 n n 其中,2和分别是事件X=-0.10、{X=0.2}和X=0.40}出现的 n 频率。当n很大时,,2和分别接近于0.1、0.7和02,于是可以期望该 nn n 机床加工出的每一个零件所获得的平均利润为
X -0.10 0.20 0.40 Y 0.1 0.7 0.2 现假设该机床加工 个零件,其中废品 件,合格品 件,优质品 件,这里 . 则这 个零件可以获得总利润为 , 平均每个零件可获利为 . 1 2 4 3 − 0.1n + 0.2n + 0. n n n n n n n1 2 3 − 0.1 + 0.2 + 0.4 n1 + n2 + n3 = n 2 n 3 n 1 n n n 其中 , 和 分别是事件 、 和 出现的 频率.当 很大时, , 和 分别接近于0.1、0.7和0.2,于是可以期望该 机床加工出的每一个零件所获得的平均利润为 n n1 n n2 n n3 {X = −0.10} {X = 0.2} {X = 0.40} n n n1 n n2 n n3

-0.1×0.1+0.2×0.7+0.4×0.2=0.21(元) 上述结果称为随机变量X的数学期望 定义1设离散型随机变量X的分布律为 X X1X2…Xk… P P1P2…Pk… 则称 E(X)=∑xxP:(要求此级数绝对收敛) k=1 为X的数学期望(或均值) 例2设X服从参数为p的(0-1)分布,求X的数学期 望. 解X的分布律为 X 0 1 P 1-p E(X)=0×(1-p)+1×p=p
− 0.10.1+ 0.20.7 + 0.40.2 = 0.21 (元) 上述结果称为随机变量X 的数学期望. 定义1 设离散型随机变量X 的分布律为 则称 (要求此级数绝对收敛) (1) 为 X 的数学期望(或均值). x1 x2 xk p1 p2 pk X P = = 1 ( ) k k pk E X x 例2 设 X 服从参数为 p 的( 0-1 )分布,求 X 的数学期 望. 解 X 的分布律为 X 0 1 P 1 - p p E(X) = 0(1− p) +1 p = p
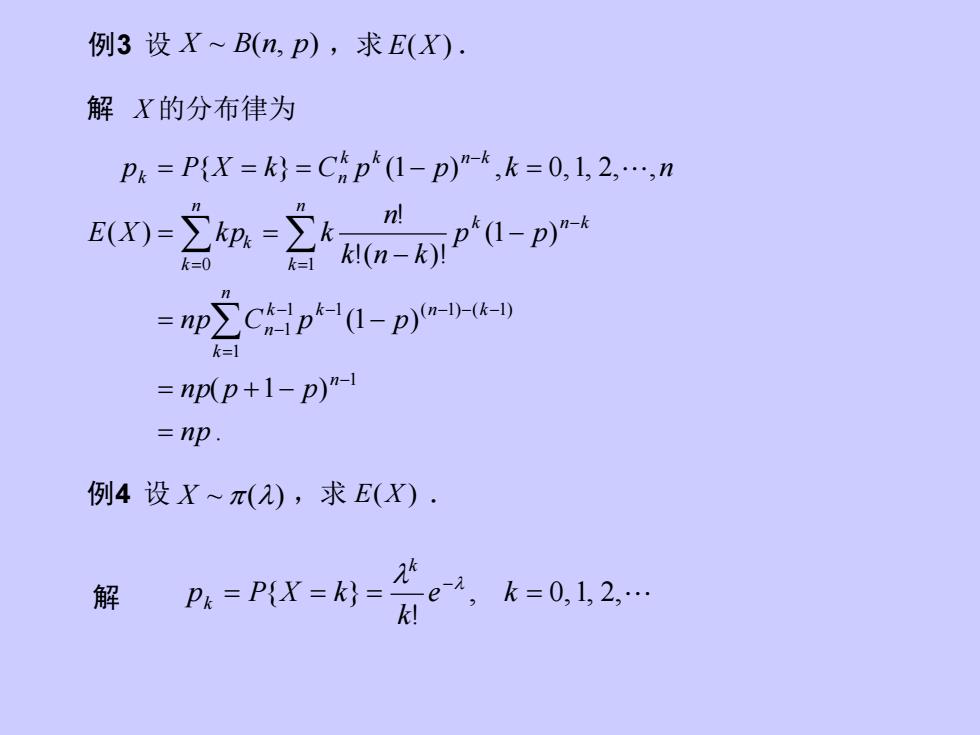
例3设X~B(n,p),求E(X). 解X的分布律为 p%=P{X=k=Cp(1-p)"-,k=0,1,2,…,n F0=空奶rI-p k=0 =np>Cp-(1-p)(-D-(-D k=1 =np(p+1-p)" =np. 例4设X~π(2),求E(X)· 解Pk=P{X=}= e,k=0,1,2,… k
例3 设 X ~ B(n, p) ,求 E(X ) . . ( 1 ) (1 ) (1 ) !( )! ! ( ) { } (1 ) , 0,1, 2, , 1 1 1 1 ( 1) ( 1) 1 0 1 n p n p p p n p C p p p p k n k n E X k p k p P X k C p p k n n n k k k n k n n k k n k n k k k k n k k n = = + − = − − − = = = = = − = − = − − − − − − = − = − 解 X 的分布律为 例4 设 X ~ () ,求 E(X ) . , 0, 1, 2, ! = { = } = = − e k k p P X k k k 解

0- k=0 名(k-1! 例5已知10件产品中有2件次品,求任意取3件中次 品数的数学期望, 解以X表示任取3件中次品的个数,可取值为0,1,2,其分布律为 8 8 8 2 3 7 2 P{X=0}= 10 15 P{X=2} 10 15 3 3 3 因此 E(X)=0x +2×1=3 15 15 155
e e . ( 1)! ! ( ) 1 1 0 1 = = − = = = − = − − = − = k k k k k k k e e k E X k p k 例5 已知10件产品中有2件次品,求任意取3件中次 品数的数学期望. , 15 1 3 10 2 2 1 8 , { 2} 15 7 3 10 1 2 2 8 , { 1} 15 7 3 10 3 8 { 0} = = = = = = = P X = = P X P X 解 以 X 表示任取3件中次品的个数,可取值为0, 1, 2,其分布律为 因此 . 5 3 15 1 2 15 7 1 15 7 E(X) = 0 + + =

二、连续型随机变量的数学期望 定义2设连续型随机变量X的概率密度为f(x), 则称 E(X)=∫f(x)dr(要求此积分绝对收敛) (2) 为X的数学期望(或均值), 例6设X在[a,b]上服从均匀分布,求E(X) 解X的概率密度为 f(x)= a≤x≤b, b-a 0, 其它 -地-= 2 例7设X服从参数为 的指数分布,求E (X)·
二、连续型随机变量的数学期望 例6 设 X 在 [ a,b ]上服从均匀分布,求E ( X ). 解 X 的概率密度为 . = − 0, . , , 1 ( ) 其它 a x b f x b a 2 d 1 ( ) ( )d a b x b a E X xf x x x b a + = − = = + − 例7 设 X 服从参数为 的指数分布,求E ( X ) . 定义2 设连续型随机变量 X 的概率密度为 f ( x ) , 则称 (要求此积分绝对收敛) 为X 的数学期望(或均值). + − E(X ) = xf (x)dx (2)

解X的概率密度为 f(x)= ex,x≥0, 0, 其它 (0-ew-,e=月 例8设X~N(4,o2),E(X) 求 解f(x)= 1-x2 ,-00<X<+00 √2πo -。 t =
解 X 的概率密度为 = − 0, . e , 0, ( ) 其它 x f x x + − + − = = = 0 1 ( ) ( )d e d E X xf x x x x x 例8 设 , 求 . ~ ( , ) 2 X N E(X ) = − + − − f x x x e , 2 1 ( ) 2 2 2 ( ) . e d 2 1 e d 2 ( )e d 2 1 e d 2 ( ) ( )d 2 2 2 2 ( ) 2 2 2 2 2 = = + + = = + − + − − − + − − + − − + − − t x x t x x x E X x f x x t t t x 解 t x = − 令

三、随机变量的函数的数学期 定1设随机变量Y是随机变量X的函数:Y=g(X); (1)若X为离散型,且分布律为p=PX=x},k=1,2,… 则 E(Y)=Eg(X]=∑g(x)Pk. (3) k= (2)若X为连续型,其密度为f(x),则 E(Y)=E[g(X)]=[g(x)f(x)dx (4) 例9设X的分布律为 X -2 -1 0 1/2 P 1/6 1/3 1/41/12 1/6 求E(X2)、E(aX+b)·
三、随机变量的函数的数学期 望 例9 设X的分布律为 X -2 -1 0 1 / 2 1 P 1 / 6 1 / 3 1 / 4 1 / 12 1 / 6 ( ) E(aX + b) 2 求 E X 、 . 定理1 设随机变量Y 是随机变量 X 的函数:Y=g(X ); (1)若X为离散型, 且分布律为 则 . pk = P{X = xk }, k =1, 2, E(Y) = E[g(X)] = = 1 ( ) k k pk g x (2)若X为连续型,其密度为f( x ),则 . + − E(Y) = E[g(X )] = g(x) f (x)dx (3) (4)

616 、 240+6. 例10设X~N(0,),求E(X2). x2 解 例11设X在区间(0,a)上服从均匀分布,求Y=kX2的数学期望, 解X的密度为f(x)= 0<x<a, a 则 其它 EY)=Ekr)=∫kxfx)=∫。kx2d=kd. 0 3
16 19 6 1 1 12 1 2 1 4 1 0 3 1 ( 1) 6 1 ( ) ( 2) 2 2 2 2 2 2 + = E X = − + − + + . 24 11 6 1 ( ) 12 1 2 1 4 1 3 1 ( ) 6 1 ( ) ( 2 ) a b E a X b a b a b b a b a b = − + + + + = − + + − + + + + 解 . 例10 设 X ~ N(0,1) ,求 E(X 2 ) . e d 1 2 1 ( ) (x)d 2 2 2 2 = = = + − + − − E X x x x x x 解 . 例11 设 X 在区间(0,a)上服从均匀分布,求 Y = kX 2 的数学期望. 解 X 的密度为 则 = 0, . , 0 , 1 ( ) 其它 x a f x a 2 0 2 2 2 3 1 d 1 ( ) ( ) ( )d x k a a E Y E k X k x f x x k x a = = = = + −

例12 设X的概率密度为 π π f(x)=2 COSX, <X< 2 2'Y=sin X,Z=cosX, 0, 其它, 求E(Y)、E(Z) 解 E(Y)=E(sin X)=sin xf(x)dx E(Z)=E(cosX)=[cosxf(x)dx -∫2cosxcosd 2 号1+c0s2xd
例12 设 X 的概率密度为 , 求 、 . − = 0, , , 2 2 cos , 2 1 ( ) 其它 x x f x Y = sin X, Z = cos X E(Y) E(Z) 解 + − E(Y) = E(sin X ) = sin xf (x)dx cos d 0 . 2 1 sin 2 2 = = − x x x . 4 d 2 1 cos2 cos d 2 1 cos ( ) (cos ) cos ( )d 2 0 2 2 = + = = = = − + − x x x x x E Z E X x f x x