
上讲提要 直接积分法 定积分的计算换元积分法 分部积分法 3
3 上 讲 提 要 定积分的计算 直接积分法 换元积分法 分部积分法

第三章 定积分的应用 一.微元法 可用条件: (1)所求量A是一个与变量x的变化区间[a,b]有关的量; (2)量A对区间具有可加性,即整体量可化成每个小区间 上的部分量之和; (3)部分量△A≈f(x)△x=f(x)dk。 基本步骤: (1)确定求的量A,由实际问题,选取一个变量x为积分 变量,并确定其变化范围[α,b]:
4 第三章 定积分的应用 一.微元法 可用条件: ⑴所求量A是一个与变量x的变化区间[ , ] a b 有关的量; (2)量A对区间具有可加性,即整体量可化成每个小区间 上的部分量之和; (3)部分量 = A f x x f x dx ( ) ( ) 。 基本步骤: (1)确定所求的量A,由实际问题,选取一个变量x为积分 变量,并确定其变化范围[ , ] a b ;

(2)x∈[a,b],给x一增量dc,(假定d>0)在[x,x+d] 上,△A≈f(x)dx,则称f(x)dx为A的微分(元),即 dA=f(x)dk。 (3)对上式积分A=∫0d4=fx)d。 二.平面图形的面积 1.y=f(x)≥0,x=a,x=b(a<b)及y=0围成的面积。 x∈[a,b],给x一增量d,在[x,x+dx]y↑ y=f(x) 上,△A≈f(x)dx,即dA=f(x)dr, 则 A=dA=f(x)d, 同理:f(x)≤0时,A=[-f(x)& xx+dx h 般情形 A=∫0f0x)1 5
5 (2) x a b [ , ] , 给 x 一 增 量 dx ,( 假 定 dx 0 ) 在 [ , ] x x dx + 上 , A f x dx ( ) , 则 称 f x dx ( ) 为 A 的 微 分 ( 元 ), 即 dA f x dx = ( ) 。 (3)对上式积分 ( ) b b a a A dA f x dx = = 。 二.平面图形的面积 1. y f x = ( ) 0,x a = ,x b a b = ( )及y = 0 围成的面积。 x a b [ , ],给 x 一增量dx ,在[ , ] x x dx + 上 , A f x dx ( ) ,即dA f x dx = ( ) , 则 ( ) b b a a A dA f x dx = = , 同理: f x( ) 0 时, [ ( )] b a A f x dx = − 一般情形 | ( ) | b a A f x dx = y o x y f x = ( ) a x x dx + b
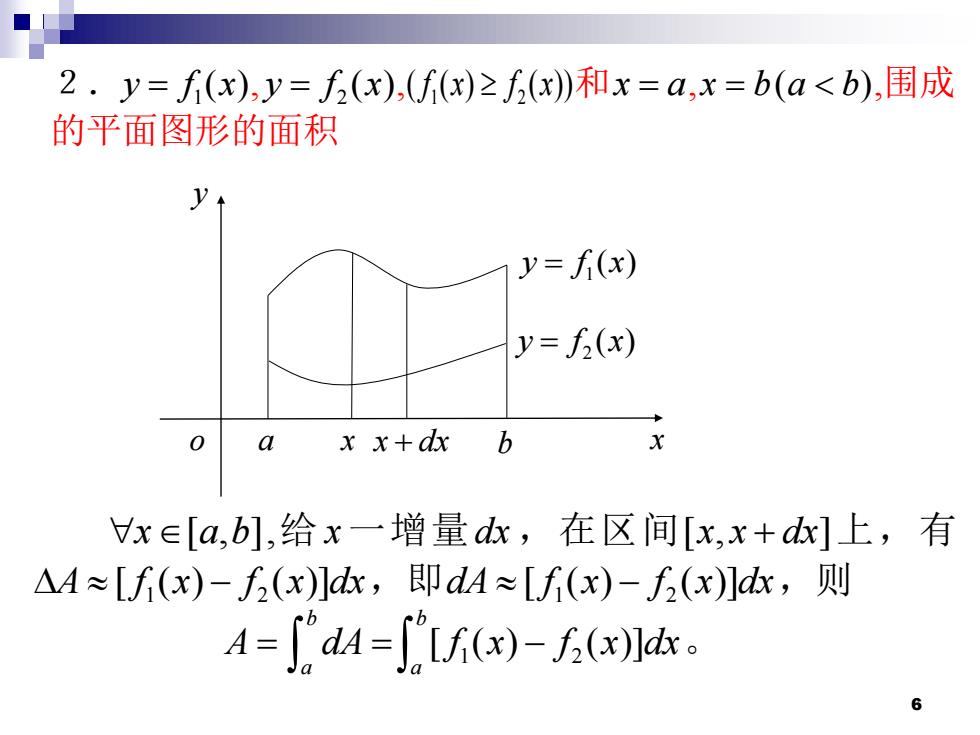
2.y=f(x),y=f(x),(f(x)≥5(x)和x=a,x=b(a<b),围成 的平面图形的面积 y=(x) y=f(x) xx+dx b x∈[a,b],给x一增量d,在区间[x,x+dx]上,有 AA≈[f(x)-f(x)]dk,即dA≈[f(x)-(x)]d,则 A=dA=Lf(x)-(xk。 6
6 2. 1 y f x = ( ), 2 y f x = ( ), 1 2 ( ( ) ( )) f x f x 和x a = ,x b = ( ) a b ,围成 的平面图形的面积 x a b [ , ],给 x 一增量dx , 在区间[ , ] x x dx + 上,有 1 2 − A f x f x dx [ ( ) ( )] ,即 1 2 dA f x f x dx − [ ( ) ( )] ,则 b a A dA = = 1 2 [ ( ) ( )] b a f x f x dx − 。 x y o 1 y f x = ( ) a x x dx + b 2 y f x = ( )

3 ·x=p(y),y=c,y=d(c<d)及x=0 围成的平面图形的面积。 y 由1的方法可得 A=@ d x=02(y) x=0(y) 4.x=0(y),x=02(y),y=C, y=d(0(y)≥p2(y),c<d)围 C 成的平面图形的面积。 x 由2的方法同理可得 A=[90)-0,0
7 3 . x y y c y d c x = = = = ( ), , ( <d) 0 及 围成的平面图形的面积。 由 1 的方法可得 ( ) d c A y dy = 4. 1 x y = ( ), 2 x y = ( ), y c = , y d = ( 1 2 ( ) ( ) y y ,c d )围 成的平面图形的面积。 由2的方法同理可得 1 2 [ ( ) ( )] d c A y y dy = − c y o x d 1 x y = ( ) 2 x y = ( )

例1.求y=3+2x-x2,y=0,x=1, x=4围成的平面图形的面积。 y=3+2x-x y y=3+2x-x1 解 得交点(-1,0),(3,0) y=0 A=1y=3+2x-x2k -1 134 =∫(3+2x-x2-∫3(3+2x-x2x -3x*r-3xrj为 6(?)召面积单位) 8
8 例1.求 2 y x x = + − 3 2 ,y = 0,x =1, x = 4围成的平面图形的面积。 解 2 3 2 0 y x x y = + − = 得交点( 1,0) − ,(3,0) 4 4 2 1 1 A y dx x x dx = = + − | | | 3 2 | 3 4 2 2 1 3 = + − − + − (3 2 ) (3 2 ) x x dx x x dx 2 3 2 3 1 1 3 4 3 3 3 3 1 3 x x x x x x = + − − + − 16 17 23 3 3 3 = − − = (面积单位) −1 o y 1 3 4 x 2 y x x = + − 3 2
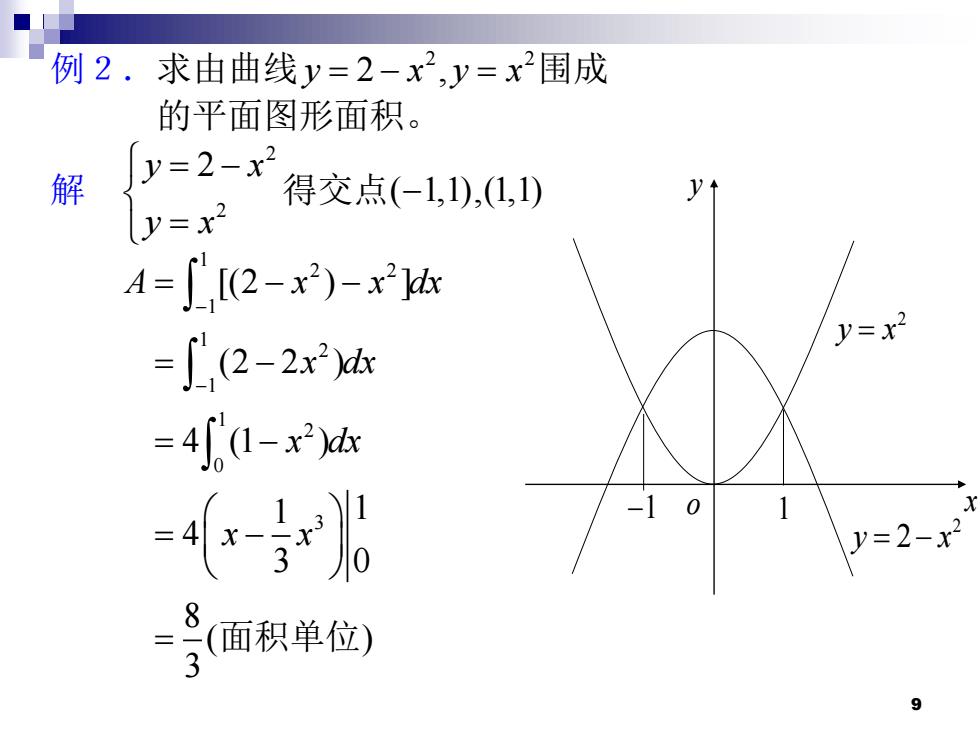
例2.求由曲线y=2-x2,y=x2围成 的平面图形面积。 解 y=2-x 得交点(-1,1),1,1) (y=x2 A=,[(2-x2)-2k y=x2 =∫(2-2x2k =41-x2x =45r8 y=2-x2 8面积华位 9
9 例2.求由曲线 2 y x = −2 , 2 y x = 围成 的平面图形面积。 解 2 2 y x 2 y x = − = 得交点( 1,1) − ,(1,1) 1 2 2 1 1 2 1 1 2 0 3 [(2 ) ] (2 2 ) 4 (1 ) 1 1 4 3 0 8 ( ) 3 A x x dx x dx x dx x x − − = − − = − = − = − = 面积单位 2 y x = −2 y −1 o x 1 2 y x =

例3.求椭圆 =1的面积S。 a b2 解 由对称性,椭圆面积S等于它在第一角限内那部分面 积的4倍。 x=asint,dx=acostdt,x=0,t=0;x=a,t= -2 S-4-asiniacosndx =4ab[cos'idt=2ab[(1+cos2t)di y↑b -2a+5n2rj月a 0 当b=a=R时,就得圆的面积S=πR。 10
10 例3.求椭圆 2 2 2 2 1 x y a b + = 的面积 S。 解 由对称性,椭圆面积S等于它在第一角限内那部分面 积的4倍。 2 2 0 4 a b S a x dx a = − 令x a t = sin ,dx a tdt = cos ,x t = = 0, 0; , 2 x a t = = 2 2 2 2 0 4 sin cos b S a a t a tdx a = − 2 2 0 4 cos ab tdt = 2 0 2 (1 cos2 ) ab t dt = + 1 2 2 sin 2 2 0 ab t t = + = ab 当b a R = = 时,就得圆的面积 2 S R = 。 y a x b o

例4.求抛物线y2=2x与直线y=x-4所围成的面积S。 解 5=+4-} 5628 S=[2x-(-v2x)k y2=2x (8,4)∠ +[v2x-(x-4] -2Z+f(-x+4)dx 8 非8 1
11 例4.求抛物线 2 y x = 2 与直线y x = − 4所围成的面积S。 解 2 4 2 4 2 y S y dx − = + − 2 3 4 4 18 2 6 2 y y y = + − = − 2 0 S x x dx = − − 2 ( 2 ) 8 2 + − − 2 ( 4) x x dx 2 8 0 2 = + − + 2 2 ( 2 4) xdx x x dx 3 3 2 2 2 4 2 2 2 1 2 8 4 18 3 3 2 0 2 x x x x = + − + = y o 2 y x = 2 y x = − 4 (8,4) (2, 2) − 8
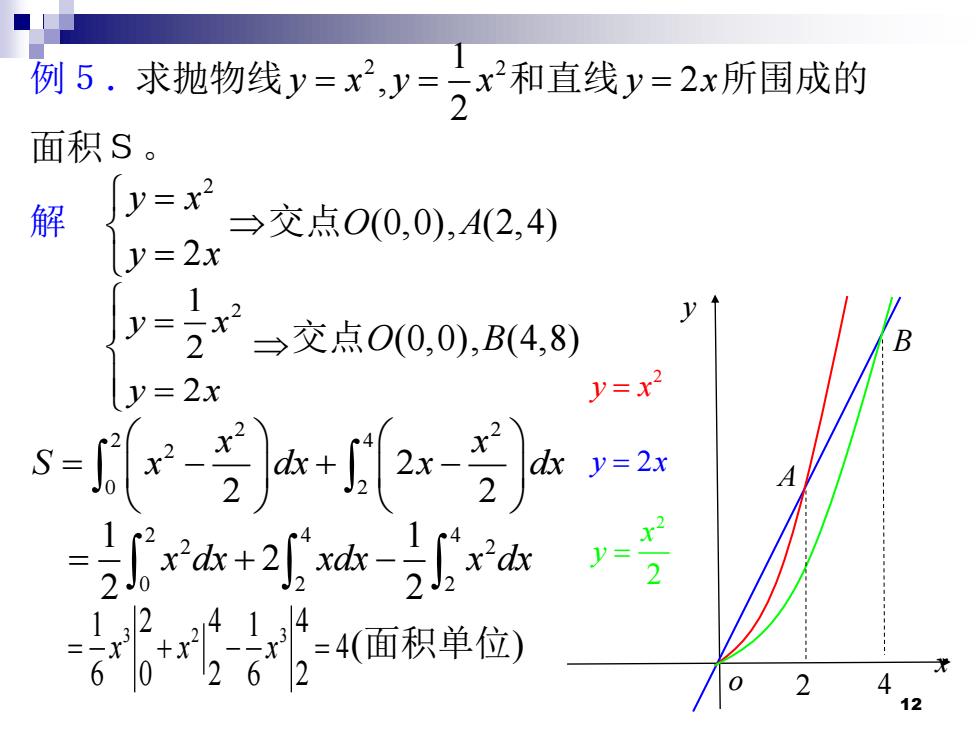
例5.求抛物线y=,y-2r和直线y=2x所围成的 面积S。 解 y=x2 →交点0(0,0),A(2,4) y=2x y= 12 X1 2 三交点O(0,0),B(4,8) y=2x y=x 2 y=2x dx+2Jxdx-Jx'dx 2 行面积单位) 13
12 例5.求抛物线 2 y x = , 1 2 2 y x = 和直线y x = 2 所围成的 面积S。 解 2 2 y x y x = = 交点O(0,0),A(2,4) 1 2 2 2 y x y x = = 交点O(0,0),B(4,8) 2 2 2 4 2 0 2 2 2 2 x x S x dx x dx = − + − 2 4 4 2 2 0 2 2 1 1 2 2 2 = + − x dx xdx x dx 3 2 3 1 1 2 4 4 4 6 6 0 2 2 = + − = x x x (面积单位) x y o 2 4 2 y x = y x = 2 2 2 x y = A B