
主讲摘要 1.复合函数求导法则; 2.隐函数求导法则,对数求导法。 3
3 主讲摘要 1.复合函数求导法则; 2.隐函数求导法则,对数求导法

第二节初等函数的导数 八、高阶导数 函数y=f(x)的导数y'=f'(x)仍然是x的函数。将 得 y'='(x)的导数,称为函数y=f(x)的二阶导数,记为 y,f"(x),9 dx2 类似,如果y”=f"(x)可导,则它的导数称为y=f(x) 的三阶数严或 dx3 若函数y=f(x)的n-1阶导数仍然可导,则它的导
4 第二节 初等函数的导数 八、高阶导数 函 数 y f x = ( )的导数 y f x = ( ) 仍然是 x 的函数。将 y f x = ( )的导数,称为函数y f x = ( )的二阶导数,记为 y , f x ( ), 2 2 d y dx 或 2 2 d f x( ) dx 类似,如果 y f x = ( )可导,则它的导数称为y f x = ( ) 的三阶导数,记为y , f x ( ), 3 3 d y dx 或 3 3 d f x( ) dx 。 若函数y f x = ( )的n −1阶导数仍然可导,则它的导

数,称为y=f(x)的n阶导数,记为 mf(x.42或f dx” x" 二阶及二阶以上的导数,统称为高阶导数。 二阶导数的物理意义 变速直线运动路程函数为S=s(t),v=s'(t)为瞬时 速度,a=v'(t)=s"(t)为加速度。 例1已知n次多项式D(x)=ax”+ax+…+an-2x2+an1x+an, 求Pn(x)的各阶导数。 解P(x)=nax+(n-1)a,x-2+…++2an-2x+a- P(x)=nn-1)a"-2+(n-10(n-2)a,x"-3+…+2an-2
5 数,称为y f x = ( )的n阶导数,记为 ( ) n y , ( ) ( ) n f x , n n d y dx 或 ( ) n n d f x dx 二阶及二阶以上的导数,统称为高阶导数。 二阶导数的物理意义 变速直线运动路程函数为s s t = ( ),v s t = ( )为瞬 时 速度,a v t s t = = ( ) ( )为加速度。 例1 已知n次多项式 1 2 0 1 2 1 ( ) n n P x a x a x a x a x a n n n n − = + + + + + − − , 求 ( ) P x n 的各阶导数。 解 1 2 0 1 2 1 ( ) ( 1) 2 n n P x na x n a x a x a n n n − − − − = + − + + + + 2 3 0 1 2 ( ) ( 1) ( 1)( 2) 2 n n P x n n a x n n a x a n n − − − = − + − − + +
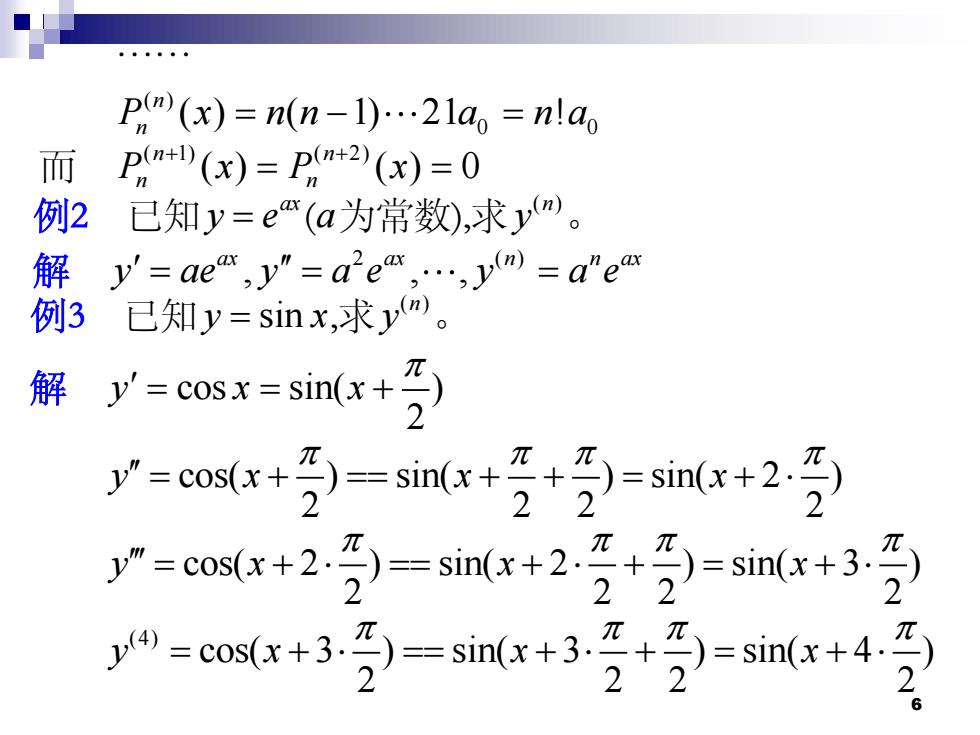
p((x)=n(n-1)...21ao=nlao 而pm+(x)=Pm2》(x)=0 例2已知y=e(a为常数),求ym。 解y'=aem,y"=ae“,…,ym=ae 例3已知y=sinx,求ym。 y=cosx=sin(x+) 解 =x+7=sm+经+=snx+2 y"=cos(x+2.7)=sin(x+2.7+7)=sin(x+3.7) π 2· =n+4 =cax+33=sn+3号+ 1
6 ……( ) 0 0 ( ) ( 1) 21 ! n P x n n a n a n = − = 而 ( 1) ( 2) ( ) ( ) 0 n n P x P x n n + + = = 例2 已知 ax y e = (a为常数),求 ( ) n y 。 解 2 ( ) , , , ax ax n n ax y ae y a e y a e = = = 例3 已知 y x = sin ,求 ( ) n y 。 解 cos sin( ) 2 y x x = = + cos( ) sin( ) sin( 2 ) 2 2 2 2 y x x x = + == + + = + cos( 2 ) sin( 2 ) sin( 3 ) 2 2 2 2 y x x x = + == + + = + (4) cos( 3 ) sin( 3 ) sin( 4 ) 2 2 2 2 y x x x = + == + + = +

y)=sin(x+n. 即nm=snx+n 同理可得(eosx=co(+n受 例4.y=ln(1+x),求y。 解 1+x (1+x)2 1.2 y"= 123 31 (1+x)3 (1+x)4 =(103 (1+x)4 7
7 …… ( ) sin( ) 2 n y x n = + 即 ( ) (sin ) sin( ) 2 n x x n = + 同理可得 ( ) (cos ) cos( ) 2 n x x n = + 例4.y x = + ln(1 ),求 ( ) n y 。 解 1 1 y x = + 2 1 (1 ) y x = − + 3 1 2 (1 ) y x = + (4) 3 4 4 1 2 3 3! ( 1) (1 ) (1 ) y x x = − = − + +

般地,有 y0=(-1)y1m-1 (1+x)” 即 nx+1o=(-1)-1n-) (1+x)” 例5已知y=ln(x+√1+x2),求y。 hz*i可 解 =apy 8
8 一般地,有 ( ) 1 ( 1)! ( 1) (1 ) n n n n y x − − = − + 即 ( ) 1 ( 1)! [ln( 1)] ( 1) (1 ) n n n n x x − − + = − + 例 5 已知 2 y x x = + + ln( 1 ) ,求 y 。 解 ( ) 2 2 1 1 1 y x x x x = + + + + 2 2 2 1 1 1 (1 ) 1 2 1 x x x x = + + + + +

中 rjj0a V(1+x2)3 例6.已知由方程y=1+x确定的函数y=f(x),求y。 解方程两边关于x求导,有 9
9 2 2 1 1 1 1 x x x x = + + + + 2 1 1 x = + y ( ) ( ) 1 3 2 2 2 2 2 1 1 1 1 2 1 2 x x x x − − = = + = − + + 2 3 (1 ) x x = − + 例6.已知由方程 1 y y xe = + 确定的函数y f x = ( ),求 y 。 解 方程两边关于x求导,有

y'=(1+xe)'=(x)'e'+xe'y =e"+xe"y' 解得y= o. 1-xe'2-y 对y'=e'+xe'y'两边关于x再求导, y"=e'y'+e"y'+xe"(y)2+xe"y" 解得y=2+yey 1-xex e (2+x, .)e y"= +1-xee1-xe_(2-xe)e2”_3-y)e2y 1-xe' (1-xe)3 (2-y)3 10
10 (1 ) ( ) y y y y y y xe x e xe y e xe y = + = + = + 解得 1 2 y y y e e y xe y = = − − 对 y y y e xe y = + 两边关于x再求导, 有 2 ( ) y y y y y e y e y xe y xe y = + + + 解得 (2 ) 1 y y xy e y y xe + = − (2 ) 1 1 1 y y y y y y e e x e xe xe y xe + − − = − 2 3 (2 ) (1 ) y y y xe e xe − = − 2 3 (3 ) (2 ) y y e y − = −

第三节微分 一。 微分的概念 (一)实例 例一边长为x的正方形的金属薄片,加热后边长由x变 到x。+△x,问此薄片的面积改变了多少? 解设此薄片的边长为x,则面积S=x2, AS=(x+△x)2-x=2x△x+(△x)月 Xo △x XoAr △x)2 △x 2x△x=AAx一△x的线性函数 lim (Ax)=limAx=0 S=62 xAx △x-→0 △x △x>0 则有(△x)2=o(△x)一△x的高阶无穷小 △S=AAx+O(△x)
11 第三节 微 分 一.微分的概念 (一)实例 例 一边长为 0 x 的正方形的金属薄片,加热后边长由 0 x 变 到 0 x x + ,问此薄片的面积改变了多少? 解 设此薄片的边长为x,则面积 2 S x = , 2 2 2 0 0 0 = + − = + S x x x x x x ( ) 2 ( ) 2 0 x x A x = —x的线性函数 2 0 0 ( ) lim lim 0 x x x x → → x = = 则有 2 ( ) x = o x ( )—x的高阶无穷小 = + s A x o x ( ) 0 x 0 x 2 S x = 0 0 x x 0 x x 2 ( ) x x x

二) 概念 定义2-2 设函数y=f(x)在x点的某邻域U(x)内有定 义,x及x+△x在该邻域U(x)内,若函数的增量可表示为 △y=A△x+o(△x) 其中A是不依赖于△x的常数,而o(△x)是当△x→0时,比 △x高阶的无穷小,则称函数那y=f(x)在点x可微,A△x 称为函数y=f(x)在x点的微分,记为dy,即dy=A△x。 实例中,△s=2x△x+(△x)2,d=2x△x=(x2)'lx=,△x (三)可导与可微的关系 定理2-3函数y=f(x)在x点可微的充分必要条件是函 数y=f(x)在点x可导,且A=f'(x)。 12
12 (二)概念 定义2-2 设函数y f x = ( )在x点的某邻域U x( )内有定 义,x及 x x + 在该邻域U x( )内,若函数的增量可表示为 = + y A x o x ( ) 其中A是不依赖于x的常数,而o x ( ) 是当 →x 0时,比 x高阶的无穷小,则称函数那 y f x = ( )在点x可微,A x 称为函数y f x = ( )在x点的微分,记为dy,即dy A x = 。 实例中, 2 2 ( ) 0 = + s x x x , 0 2 ds x x x x 2 ( ) | 0 x x = = = (三)可导与可微的关系 定理2-3 函数y = f x( )在x点可微的充分必要条件是函 数y f x = ( )在点x可导,且A f x = ( )