
第26卷第3期 萍乡高等专科学校学报 2009年6月 Vol 26 NO.3 Journal of Pingxiang College Jun 2009 小学数学奥赛试题解再评析 李幼年 (萍乡高等专科学校,江西萍乡337000) 摘要:指出小学数学奥林匹克党赛(全国联赛)试题解的一些错误并进行了补正,分析了试题解的某些不足之处。提 出了既能反映奥赛宗旨,又结合小学和初中数学教学实际的思路和方法。 关键词分析过程逻辑推理损益法相间插空法 中图分类号:G6245文献标识码A文章编号:1007.9149(2009)03.0001.07 1分析过程有误,解法缺乏新意 例如:2004年决赛试卷第11题。图1所示,在 B-S之HE-bE,NE-子×E- △ABC中,CD、AE,BF分别为BC,CAAB长的3 BE,∴SAN=7S△E=子X】SAC=,同理可得 那么S△MNP:S△BC= S△E=2SAc,∴Sa边形AEr=子】--2于 Sam=k子子子子故-221 笔者课“分析所述错误甚多①是-肥。子 即。子:这里就肯定CE-2,这就错了,因为只 知道氏=子,不一定CE等于2②如果“分析"中的 推导都成立的话.S2=1:子寸子又不对了, 应该是SaSa,因为试题说 的是任意三角形ABC,就是所有的三角形按照题目 的条件作出的△MNP与△ABC面积的比是个常数, 图1 要求出这个常数,所以为了简化推导是过程,不妨设 答案221. 这个三角形是边长为6的等边△4BC,如图2所示。 分析作DH/AC交BE于H,侧是肥-子 分别在ABBC、CA上取BF=CD=AE=6X=2, 即P=子所以DH=手在△DHN和△ANE中, 连BE、CF、AD且两两相交于PM、N,作FK⊥BC 于K,作PG⊥BC于G,连ED,则FK/PG/AH,令 DHE,R是-即子-NE=HE, AH=h,则KC-5,BD=4,FK-h,ED=h,有 收稿日期2008.10-10 作者简介:李幼年(1928一,男.江西丰城人,中师特级教师,中专高级讲师、主要从事数学教学方而的研究 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://vww.cnki.ne
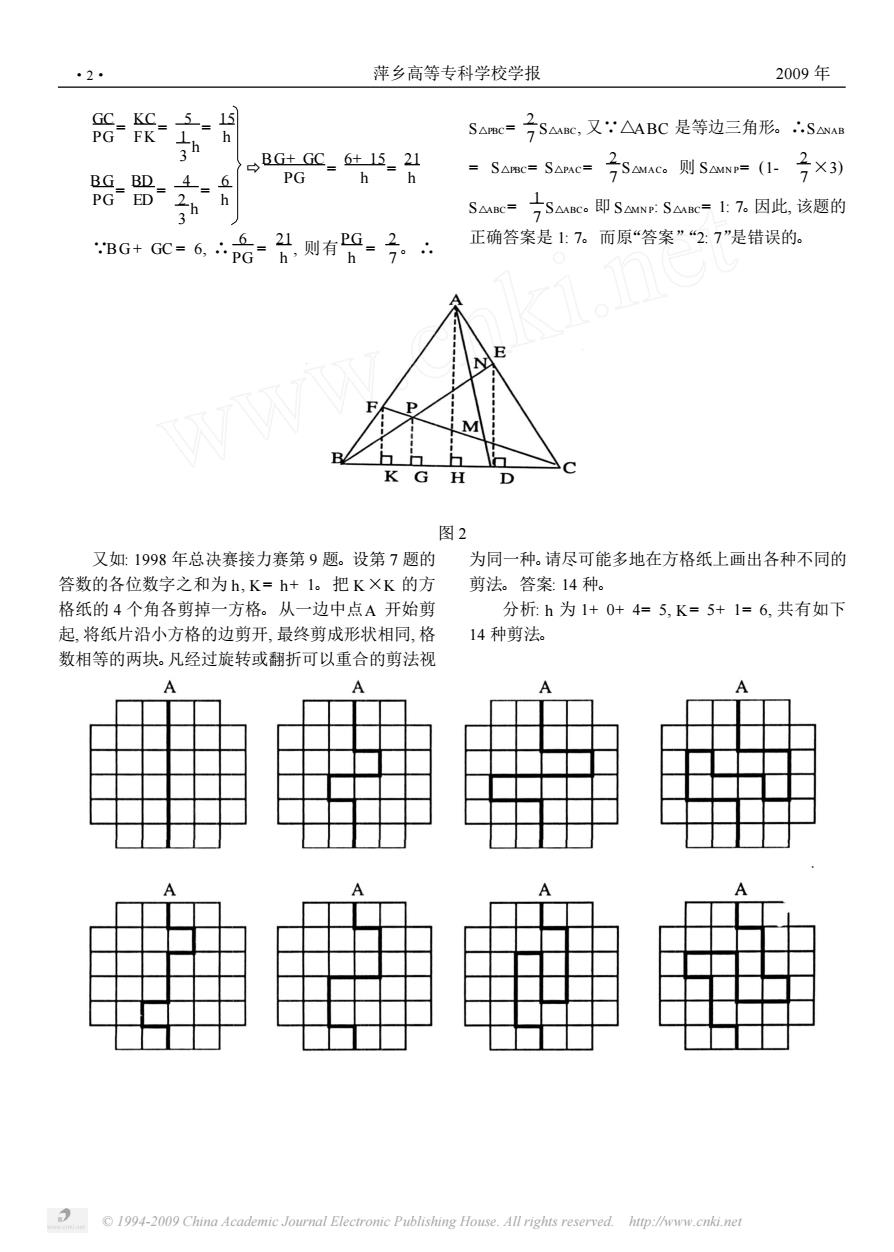
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 第 26 卷第 3 期 Vo l. 26 NO. 3 萍乡高等专科学校学报 Jou rnal of Pingx iang Co llege 2009 年 6 月 Jun. 2009 小学数学奥赛试题解再评析 李 幼 年 (萍乡高等专科学校, 江西 萍乡 337000) 摘 要: 指出小学数学奥林匹克竞赛(全国联赛) 试题解的一些错误并进行了补正, 分析了试题解的某些不足之处。提 出了既能反映奥赛宗旨, 又结合小学和初中数学教学实际的思路和方法。 关键词: 分析过程; 逻辑推理; 损益法; 相间插空法 中图分类号: G624. 5 文献标识码: A 文章编号: 1007- 9149 (2009) 03- 0001- 07 1 分析过程有误, 解法缺乏新意 例如: 2004 年决赛试卷第 11 题。图 1 所示, 在 △ABC 中, CD、A E、BF 分别为BC、CA、AB 长的 1 3 , 那么 S△MN P: S△ABC= : 。 图 1 答案: 2: 21。 分析: 作DHööA C 交BE 于H , 则 DH CE = BD BC = 2 3 , 即 DH 2 = 2 3 , 所以DH = 4 3 。在△DHN 和△AN E 中, DHööA E, ∴ DH A E = HN N E , 即 4 3 1 = N H N E , ∴N E = 3 7 H E, ∵ H E BH = DC BD = 1 2 , H E= 1 3 BE, ∴N E= 3 7 × 1 3 BE= 1 7 BE, ∴S△AN E = 1 7 S△ABE = 1 7 × 1 3 S△ABC = 1 21 , 同理可得 S△PBF = 1 21 S△ABC, ∴S四边形 A EPF = 1 3 - 1 21 - 1 21 = 5 21 , S△MN P= 1- 1 3 - 1 3 - 5 21 = 2 21 , 故 S△MN P: S△ABC= 2: 21。 笔者评:“分析”所述错误甚多: ①“ DH CE = BD BC = 2 3 即 DH 2 = 2 3 ”, 这里就肯定 CE= 2, 这就错了, 因为只 知道 CE EA = 2 1 , 不一定 CE 等于 2; ②如果“分析”中的 推导都成立的话, S△MN P= 1- 1 3 - 1 3 - 5 21 又不对了, 应该是 S△MN P= 1- 1 3 - 1 3 - 5 21 + S△MDC。因为试题说 的是任意三角形ABC, 就是所有的三角形按照题目 的条件作出的△M N P 与△ABC 面积的比是个常数, 要求出这个常数, 所以为了简化推导是过程, 不妨设 这个三角形是边长为 6 的等边△ABC, 如图 2 所示。 分别在AB、BC、CA 上取BF= CD = A E= 6× 1 3 = 2, 连BE、CF、AD 且两两相交于 P、M、N , 作 FK⊥BC 于 K, 作 PG⊥BC 于 G, 连 ED , 则 FKööPGööA H , 令 A H = h, 则 KC= 5,BD = 4, FK= 1 3 h, ED = 2 3 h, 有 收稿日期: 2008- 10- 10 作者简介: 李幼年(1928—) , 男, 江西丰城人, 中师特级教师, 中专高级讲师, 主要从事数学教学方面的研究
2 萍乡高等专科学校学报 2009年 h SAmc=子SAC,又:△ABC是等边三角形。SANA BG+.2 PG =S△c=SAA=SAAc。则S=(I.子X3) S△C=SAc,即=上,因此,该愿的 BG+GC=6亮=则有-子· 正确答案是上:7。而原“答案”“27”是错误的。 图2 又如1998年总决赛接力赛第9题。设第7题的 为同一种。请尽可能多地在方格纸上画出各种不同的 答数的各位数字之和为h,K=h+l。把KXK的方 剪法。答案14种。 格纸的4个角各剪掉一方格。从一边中点A开始剪 分析:h为1+0叶4=5,K=5+1=6,共有如下 起,将纸片沿小方格的边剪开,最终剪成形状相同,格 14种剪法。 数相等的两块。凡经过旋转或翻折可以重合的剪法视 A A 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.hup://ww.cnki.net
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net GC PG = KC FK = 5 1 3 h = 15 h BG PG = BD ED = 4 2 3 h = 6 h ⊥ BG+ GC PG = 6+ 15 h = 21 h ∵BG + GC = 6, ∴ 6 PG = 21 h , 则有 PG h = 2 7 。 ∴ S△PBC= 2 7 S△ABC, 又∵△ABC 是等边三角形。∴S△NAB = S△PBC= S△PAC= 2 7 S△MAC。则 S△MN P= (1- 2 7 ×3) S△ABC= 1 7 S△ABC。即 S△MN P: S△ABC= 1: 7。因此, 该题的 正确答案是 1: 7。而原“答案”“2: 7”是错误的。 图 2 又如: 1998 年总决赛接力赛第 9 题。设第 7 题的 答数的各位数字之和为 h, K= h+ 1。把 K×K 的方 格纸的 4 个角各剪掉一方格。从一边中点A 开始剪 起, 将纸片沿小方格的边剪开, 最终剪成形状相同, 格 数相等的两块。凡经过旋转或翻折可以重合的剪法视 为同一种。请尽可能多地在方格纸上画出各种不同的 剪法。答案: 14 种。 分析: h 为 1+ 0+ 4= 5, K= 5+ 1= 6, 共有如下 14 种剪法。 ·2· 萍乡高等专科学校学报 2009 年
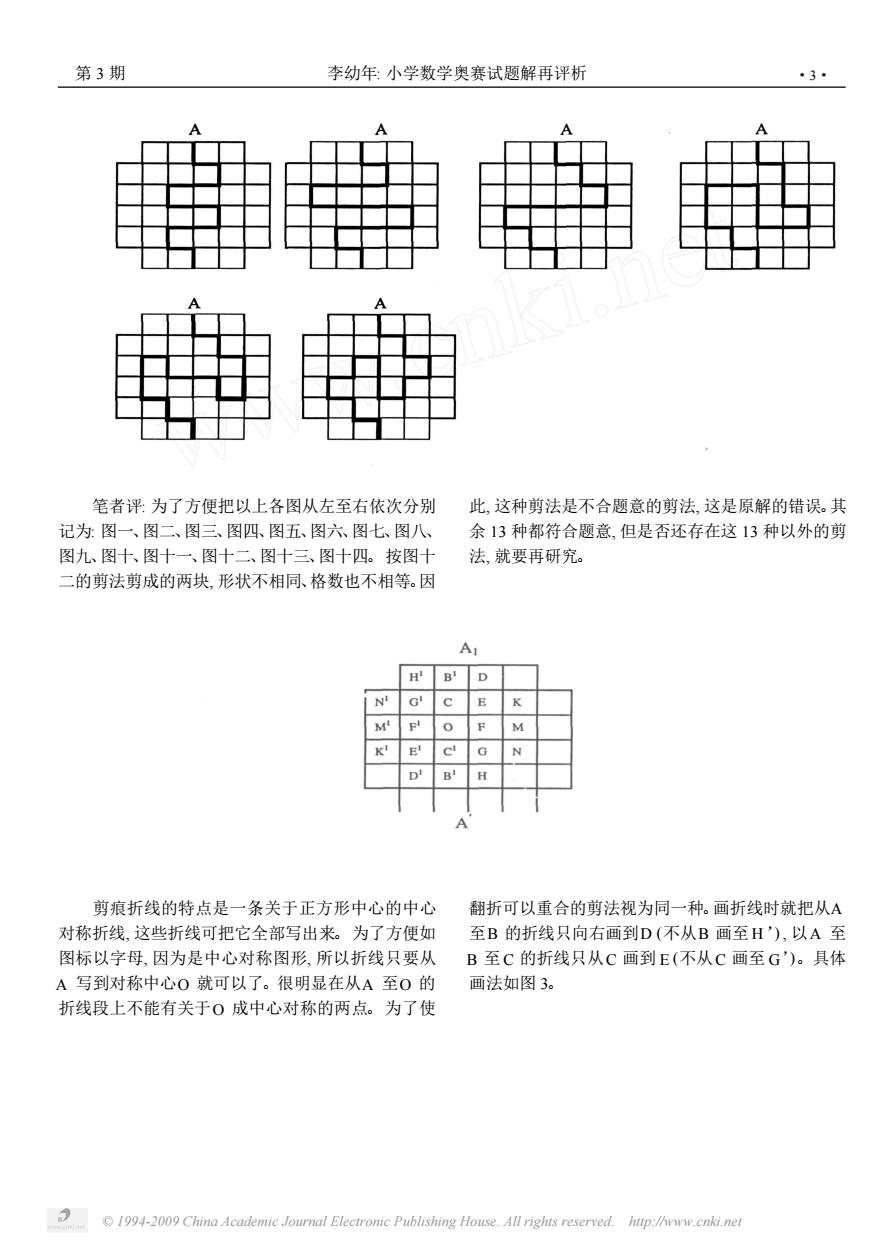
第3期 李幼年:小学数学奥赛试题解再评析 3· 笔者评为了方便把以上各图从左至右依次分别 此,这种剪法是不合题意的剪法,这是原解的错误。其 记为:图一、图二、图三、图四、图五、图六图七、图八、 余13种都符合题意,但是否还存在这13种以外的剪 图九、图十、图十一、图十二、图十三、图十四。按图十 法,就要再研究。 二的剪法剪成的两块,形状不相同、格数也不相等。因 N 剪痕折线的特点是一条关于正方形中心的中心 翻折可以重合的剪法视为同一种。画折线时就把从A 对称折线.这些折线可把它全部写出来。为了方便如 至B的折线只向右画到D(不从B画至H'),以A至 图标以字母,因为是中心对称图形,所以折线只要从 B至C的折线只从C画到E(不从C画至G')。具体 A写到对称中心0就可以了。很明显在从A至0的 画法如图3。 折线段上不能有关于0成中心对称的两点。为了使 14-09 Chn Academe ou Eerom Pbn Hollighs sedp
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 笔者评: 为了方便把以上各图从左至右依次分别 记为: 图一、图二、图三、图四、图五、图六、图七、图八、 图九、图十、图十一、图十二、图十三、图十四。按图十 二的剪法剪成的两块, 形状不相同、格数也不相等。因 此, 这种剪法是不合题意的剪法, 这是原解的错误。其 余 13 种都符合题意, 但是否还存在这 13 种以外的剪 法, 就要再研究。 剪痕折线的特点是一条关于正方形中心的中心 对称折线, 这些折线可把它全部写出来。为了方便如 图标以字母, 因为是中心对称图形, 所以折线只要从 A 写到对称中心O 就可以了。很明显在从A 至O 的 折线段上不能有关于O 成中心对称的两点。为了使 翻折可以重合的剪法视为同一种。画折线时就把从A 至B 的折线只向右画到D (不从B 画至 H’) , 以A 至 B 至C 的折线只从C 画到 E (不从C 画至 G’)。具体 画法如图 3。 第 3 期 李幼年: 小学数学奥赛试题解再评析 ·3·
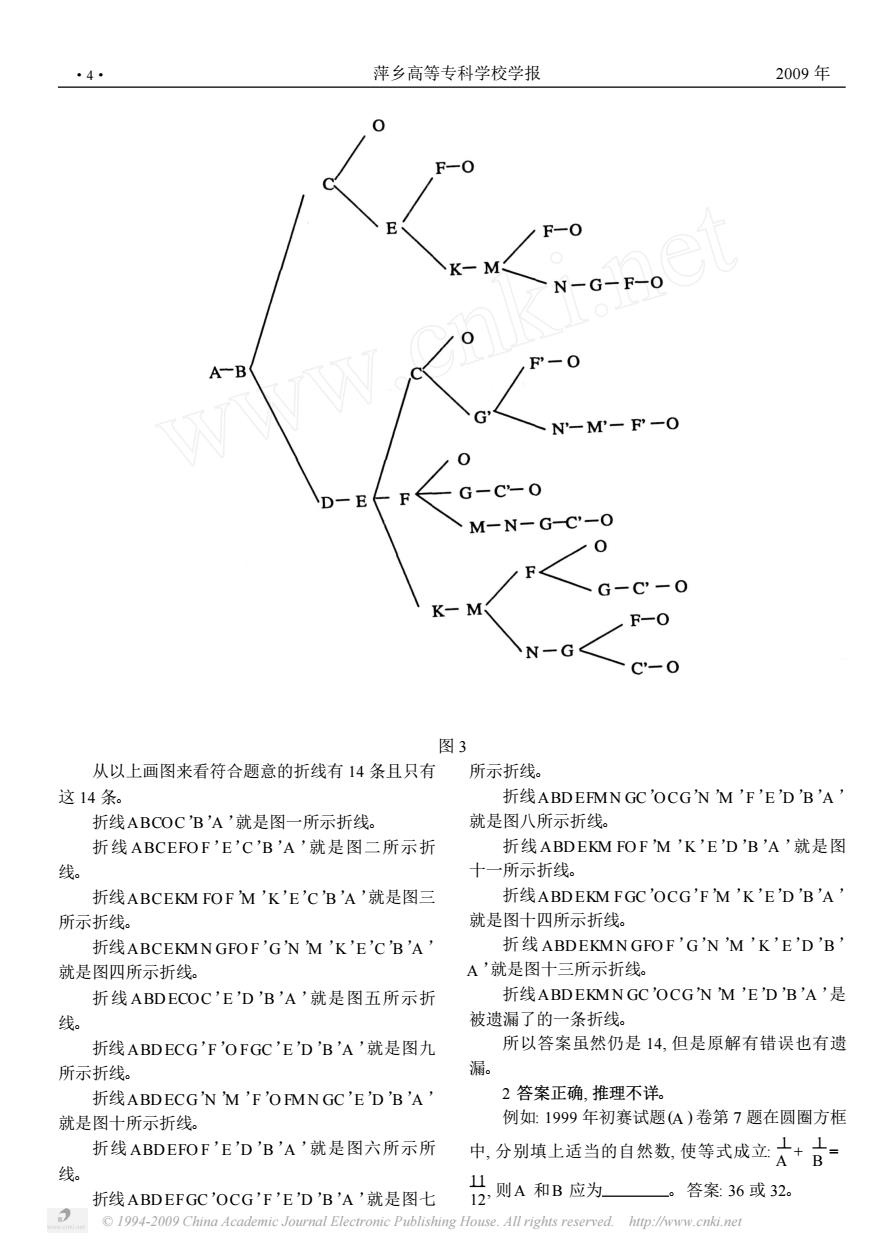
·4 萍乡高等专科学校学报 2009年 0 F-O A 、N-Mr-F'-O G-c-0 M-N-G-C-0 、G-C-0 .F-0 N-G< c-0 图3 从以上画图来看符合题意的折线有14条且只有 所示折线。 这14条。 折线ABDEFMN GC'OCG'N'M'F'ED'B'A' 折线ABCOC'B'A'就是图一所示折线。 就是图八所示折线。 折线ABCEFOF'E'CB'A'就是图二所示折 折线ABDEKM FOF'M'K'ED'B'A'就是图 线。 所示折线。 折线ABCEKM FOF'M'K'E'CB'A'就是图三 折线ABDEKMFGC'OCG'FM'K'EDB'A' 所示折线。 就是图十四所示折线。 折线ABCEKMN GFOF'G'NM'K'E'CB'A' 折线ABDEKMNGFOF'G'NM'K'E'D'B 就是图四所示折线 A'就是图十三所示折线。 折线ABDECOC'E'D'B'A'就是图五所示折 折线ABDEKMN GC'OCG'N'M'EDB'A'是 爱 被遗漏了的一条折线。 折线ABDECG'F'OFGC'EDB'A'就是图九 所以答案虽然仍是14,但是原解有错误也有遗 所示折线。 折线ABDECG'N 'M'F'OFMNGC'EDB'A' 2答案正确,推理不详。 就是图十所示折线。 例如:1999年初赛试题(A)卷第7题在圆圈方框 折线ABDEFOF'E'D'B'A'就是图六所示所 中,分别填上适当的自然数,使等式成立人+古 折线ABDEFGC'OCG'F'EDB'A'就是图七 片则A和B应为 。答案36或32。 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 图 3 从以上画图来看符合题意的折线有 14 条且只有 这 14 条。 折线ABCOC’B’A ’就是图一所示折线。 折线 ABCEFO F’E’C’B’A ’就是图二所示折 线。 折线ABCEKM FO F’M ’K’E’C’B’A ’就是图三 所示折线。 折线ABCEKM N GFO F’G’N ’M ’K’E’C’B’A ’ 就是图四所示折线。 折线 ABD ECOC’E’D ’B’A ’就是图五所示折 线。 折线ABD ECG’F’O FGC’E’D ’B’A ’就是图九 所示折线。 折线ABD ECG’N ’M ’F’O FM N GC’E’D ’B’A ’ 就是图十所示折线。 折线ABD EFO F’E’D ’B ’A ’就是图六所示所 线。 折线ABD EFGC’OCG’F’E’D ’B’A ’就是图七 所示折线。 折线ABD EFM N GC’OCG’N ’M ’F’E’D ’B’A ’ 就是图八所示折线。 折线ABD EKM FO F’M ’K’E’D ’B ’A ’就是图 十一所示折线。 折线ABD EKM FGC’OCG’F’M ’K’E’D ’B’A ’ 就是图十四所示折线。 折线 ABD EKM N GFO F’G’N ’M ’K’E’D ’B ’ A ’就是图十三所示折线。 折线ABD EKM N GC’OCG’N ’M ’E’D ’B’A ’是 被遗漏了的一条折线。 所以答案虽然仍是 14, 但是原解有错误也有遗 漏。 2 答案正确, 推理不详。 例如: 1999 年初赛试题(A ) 卷第 7 题在圆圈方框 中, 分别填上适当的自然数, 使等式成立: 1 A + 1 B = 11 12 , 则A 和B 应为 。答案: 36 或 32。 ·4· 萍乡高等专科学校学报 2009 年

第3期 李幼年:小学数学奥赛试题解再评析 5。 分析:令A=x,B=y,则有:11xy-12y=29× 3.“某数除以13余10”即某数比13的倍数少3.可 12x,y1x.2)=29×12x,y=%由于丈 知某数比1山和13的公倍数少3。令x为整数,则某 数可表示为11X13x.3=143x.3.又令v为整数 +29片那么y必大于30,经试算y可取32和36 可知某数为17y+12,于是143x-3=17y+12,y= 笔者评“分析”中提出“y必大于30,经试算y可 143 7 取32或36。” 5=81+,不难看出,当x=7时,y =58。∴,这个数的最小可能值是143×7.3=998。 要知道大于30的自然数多的是,但不知要经过 怎样的试算,也不知经过了多少次的试算才能确定这 又如1997年总决赛数学竞赛第10题。有一座山 32和36更不知除此以外是否还存在满足条件的自 里有若干个大和尚和若干个小和尚,已知7个大和治 然数?这里作如下探计由“分析可知y一品合 每天共吃41个馒头,29个小和尚每天共吃11个馒 头,而平均每个和尚每天恰好吃一个馒头,那么在这 座山里至少有和尚 个。答案556个。 11x-1 分析:(不定方程法)设有x个大和尚,y个小和 尚,每个大和尚吃馒头!个,每个小和尚吃馒头 知72必为自然数,且1x12必为4176的 个,x个大和尚和y个小和尚吃馒头的个数为号个, 个因数,然而4176=1×4176=2×2088=3×1392 每个小和尚吃馒头个,x个大和尚和y个小和尚吃 4×1044■6×696■8×522■9×464■12×348■16 ×261=18×232=24×174=29×14436×116=48 馒头的个数为)x+马y(个),因为每人恰好吃一个 ×87=58×72。即4176共有30个因数,即11x-12 的值只能是这30个因数中的一个或几个。经试算可 所以馒头个数等于和尚个数由此可列出方程x+ 知当11x-12=87时,x=9,y=36,当11x-12= 0=X+y解得x=站×,所以共有和尚数是x+ 1044时×=96,y=32。其余28个因数都不能得出满 足条件的解。故可确定A,B应填的只能是36或32。 y=8×+y=的,因为人数为整数所以x+y 3条件挖据不够,解法并非最简 例如:1998年初赛试题A)第6题。某数除以11 为整数,观察的y后,只有总为整数x+y才可能 余8,除以13余10,除以17余12,那么这个数的最小 为整数,所以推得y~493,进一步得到x~是×子× 可能值是 ,答案998。分析这类题一般用枚 493=63.所以和尚数为x+y=63+493=556(个)。 举法来解、其解题步骤是:(1)先列出多个“被几除余 笔者评“答案”正确“分析”合理,过程也不太繁。 几"的数串,(2)所有数串中第 一个公有的数就是符合 但“平均”这条件利用不充分,可用这条件求出大、小 条件的第一个数。但有时需要写出较长的数串比较 和尚人数比的“损益法”。 麻烦,这也正是枚举法的弱点,遇到较复杂的问题时, 如果平均每个和尚每天恰好吃一个馒头,那么, 可对枚举法作些改进先找出除以17余12的数29, 46,63,80,97,114,113,,(从除数较大的开始找, 每个大和尚每天都少吃(受损)号1=兰个,每个小 比较方便)。再找出除13余10的数23,36,49,62 和尚每天都多吃(受益)1。=8个。要满足平均 75,88,101,114,…,显然114满足被17除余12, 数,只须使多吃的个数等于少吃的个数,又只须取大 被13除余10。由于17和13的最小公倍数是221.所 小和尚人数的比等于大小和尚受损、受益个数的反比 以114+221×1,114+221×2,114+221×3,114 221×4,114+221×5,…,均满足被17除余12,被 号斗63493,而63493是最简的比,所以大小和 13除余10。只需在这串数中找到除以11余8的数就 尚至少有63+493=556个。 行了,显然114+221X4998符合题意。 又如:1997年初赛试题B)第8题两个杯中分 笔者评“分析”没有发现一个隐性条件,所以解 别装有浓度40%与10%的食盐水,倒在一起后混合 法比较麻烦 食盐水浓度为30%。若再加入300克20%的食盐水 因为“某数除以11余8”即某数比11的倍数少 则浓度变成25%,那么原有40%的食盐水
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 分析: 令A = x, B = y, 则有: 11xy - 12y= 29× 12x, y×(11x- 12) = 29×12x, y= 29 ×12x 11x- 12 , 由于 1 x + 29 y = 11 12 , 那么 y 必大于 30, 经试算 y 可取 32 和 36。 笔者评:“分析”中提出“y 必大于 30, 经试算 y 可 取 32 或 36。” 要知道大于 30 的自然数多的是, 但不知要经过 怎样的试算, 也不知经过了多少次的试算才能确定这 32 和 36, 更不知除此以外是否还存在满足条件的自 然数? 这里作如下探讨: 由“分析”可知 y= 29 ×12x 11x- 12 = 348x 11x- 12 = 31 + 7x+ 372 11x- 12 , 则 11y = 31 × 11 + 7x+ 372 11x- 12 ×11= 341+ 77x+ 4092 11x- 12 = 348+ 4176 11x- 12 。可 知 4176 11x- 12 必为自然数, 且 11x - 12 必为 4176 的一 个因数, 然而 4176= 1×4176= 2×2088= 3×1392= 4×1044= 6×696= 8×522= 9×464= 12×348= 16 ×261= 18×232= 24×174= 29×144= 36×116= 48 ×87= 58×72。即 4176 共有 30 个因数, 即 11x- 12 的值只能是这 30 个因数中的一个或几个。经试算可 知当 11x - 12= 87 时, x = 9, y = 36, 当 11x - 12= 1044 时 x= 96, y= 32。其余 28 个因数都不能得出满 足条件的解。故可确定A、B 应填的只能是 36 或 32。 3 条件挖掘不够, 解法并非最简 例如: 1998 年初赛试题(A ) 第 6 题。某数除以 11 余 8, 除以 13 余 10, 除以 17 余 12, 那么这个数的最小 可能值是 。答案 998。分析: 这类题一般用枚 举法来解, 其解题步骤是: (1) 先列出多个“被几除余 几”的数串, (2) 所有数串中第一个公有的数就是符合 条件的第一个数。但有时需要写出较长的数串, 比较 麻烦, 这也正是枚举法的弱点, 遇到较复杂的问题时, 可对枚举法作些改进: 先找出除以 17 余 12 的数: 29, 46, 63, 80, 97, 114, 113, ……, (从除数较大的开始找, 比较方便)。再找出除 13 余 10 的数: 23, 36, 49, 62, 75, 88, 101, 114, ……, 显然 114 满足被 17 除余 12, 被 13 除余 10。由于 17 和 13 的最小公倍数是 221, 所 以 114+ 221×1, 114+ 221×2, 114+ 221×3, 114+ 221×4, 114+ 221×5, ……, 均满足被 17 除余 12, 被 13 除余 10。只需在这串数中找到除以 11 余 8 的数就 行了, 显然 114+ 221×4= 998 符合题意。 笔者评:“分析”没有发现一个隐性条件, 所以解 法比较麻烦。 因为“某数除以 11 余 8”, 即某数比 11 的倍数少 3,“某数除以 13 余 10”, 即某数比 13 的倍数少 3, 可 知某数比 11 和 13 的公倍数少 3。令 x 为整数, 则某 数可表示为 11×13x - 3= 143x - 3, 又令 y 为整数, 可知某数为 17y+ 12, 于是 143x - 3= 17y+ 12, y= 143x- 15 17 = 8x- 1+ 7x+ 2 17 , 不难看出, 当 x= 7 时, y = 58。∴这个数的最小可能值是 143×7- 3= 998。 又如 1997 年总决赛数学竞赛第 10 题。有一座山 里有若干个大和尚和若干个小和尚, 已知 7 个大和尚 每天共吃 41 个馒头, 29 个小和尚每天共吃 11 个馒 头, 而平均每个和尚每天恰好吃一个馒头, 那么在这 座山里至少有和尚 个。答案: 556 个。 分析: (不定方程法) 设有 x 个大和尚, y 个小和 尚, 每个大和尚吃馒头 41 7 个, 每个小和尚吃馒头 11 29 个, x 个大和尚和 y 个小和尚吃馒头的个数为 41 7 个, 每个小和尚吃馒头 11 29 个, x 个大和尚和 y 个小和尚吃 馒头的个数为 41 7 x+ 11 29 y (个) , 因为每人恰好吃一个, 所以馒头个数等于和尚个数, 由此可列出方程 41 7 x+ 11 29 y= x+ y 解得 x= 11 29 × 7 17 y, 所以共有和尚数是x+ y= 11 29 × 7 17 y+ y= 556 493 y, 因为人数为整数, 所以 x+ y 为整数, 观察 556 493 y 后, 只有 556 493 y 为整数, x+ y 才可能 为整数, 所以推得 y= 493, 进一步得到 x= 9 29 × 7 17 × 493= 63, 所以和尚数为 x+ y= 63+ 493= 556 (个)。 笔者评:“答案”正确“分析”合理, 过程也不太繁。 但“平均”这条件利用不充分, 可用这条件求出大、小 和尚人数比的“损益法”。 如果平均每个和尚每天恰好吃一个馒头, 那么, 每个大和尚每天都少吃(受损) 41 7 - 1= 34 7 个, 每个小 和尚每天都多吃(受益) 1- 11 29 = 18 29 个。要满足平均 数, 只须使多吃的个数等于少吃的个数, 又只须取大 小和尚人数的比等于大小和尚受损、受益个数的反比 18 29 : 34 7 = 63: 493, 而 63: 493 是最简的比, 所以大小和 尚至少有 63+ 493= 556 个。 又如: 1997 年初赛试题 (B) 第 8 题 两个杯中分 别装有浓度 40% 与 10% 的食盐水, 倒在一起后混合 食盐水浓度为 30%。若再加入 300 克 20% 的食盐水, 则浓度变成 25% , 那么原有 40% 的食盐水 第 3 期 李幼年: 小学数学奥赛试题解再评析 ·5·

·6… 萍乡高等专科学校学报 2009年 克。答案200克。分析浓度为30%与20%的食盐水 30%.受益20%。为了使损与益相竿这两种量这出 应该是10%与20%的反比,即2:1。原有40%的食 盐为300×)=200克。“损益法"其实是一种口算 的食盐水有300克。设原有40%的食盐x克,则有 10%的食盐(300-x)克,依题意可列方程x×40% 法,有的题运用损益法非常简捷。 +(300-x)×10%=300×30%的解之得x=200.即 4“特殊”代替“一般”,逻辑推理错误 例如:2000年初赛试题(4)卷第12题,有8级台 原有40%的食盐水200克。 笔者评题中所述“浓度为30%”30%就是“平 阶,小明从下向上走,若每次只能跨一级或两级他走 均数”,因此也可用前例中所说的“损益法”解,其实 上去可有 一种不同方法。 答案34。 “分折”中所说的:“40%与10%的食盐水混合成30% 的食盐水有300克”就是用了“损益法得出的,就不 分析:先看一级、二级、三级台阶各有几种不同的 详叙了。只说用“损益法”求“原有40%的食盐水200 跨法 克”。40%的要降为30%,受损10%。10%的要升为 有二种不同跨法 只有一种跨法 ③再画出三级台阶,易发现有五种不同跨法,若 5=3+2,”两个特例就得出一般情况,即所谓“规律” 四级台阶呢?也不难发现有三种不同跨法,将台阶级 是很不够的,即使有更多的特例也只能说是个经验命 数与对应的不同跨法排成下表就会有所发现。 题或猜想命题、这类命题。在没有经过逻辑推论前是 台阶级数12345·8 不能作为论据的。所以“分析中所得出的答案是否可 不同跨法12358… 靠值得怀疑。因此,提出用相间插空法来解 规律已显现在眼前,1,2,3(=2+1),5(=3+2), 不同的跨法分为五类 8(=5+3),13(8+5),21-(13+8),34(=21+ (一)四次都跨两级走上去,只有1种跨法 13),即为1、2345678级台阶的不同跨法,所以 (二)三次跨两级二次跨一级走上去,为了方便这 有8级台阶,每跨一级域两级共有34种不同的方法。 里用一个“双”字表示一次跨两级,用一个“单”字表示 笔者评“分析”中所说的“规律”仅凭“3=2+1, 一次跨一级,这里又分两种情况 A:单单双 双 双 单单 双 双 双 单单 双 双 单单 B: 单 双 单 单 单 双双 单 双双 单 单 双双 双双 单 双 单 单 这一类两种情况共有4+6=10种跨法。 1994- 009 China Academic Journal Electronic Publishing House.All rights reserved. htp://www.cnki.net
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 克。答案: 200 克。分析: 浓度为 30% 与 20% 的食盐水 若混合成 25% 的食盐水, 则 30% 与 20% 的食盐水质 量应该相同, 所以 40% 与 10% 的食盐水混合成 30% 的食盐水有 300 克。设原有 40% 的食盐 x 克, 则有 10% 的食盐 (300- x) 克, 依题意可列方程: x×40% + (300- x) ×10% = 300×30% 的解之得 x= 200, 即 原有 40% 的食盐水 200 克。 笔者评: 题中所述“浓度为 30% ”, 30% 就是“平 均数”, 因此也可用前例中所说的“损益法”解, 其实 “分析”中所说的:“40% 与 10% 的食盐水混合成 30% 的食盐水有 300 克”。就是用了“损益法”得出的, 就不 详叙了。只说用“损益法”求“原有 40% 的食盐水 200 克”。40% 的要降为 30% , 受损 10%。10% 的要升为 30% , 受益 20%。为了使损与益相等, 这两种量这比 应该是 10% 与 20% 的反比, 即 2: 1。∴原有 40% 的食 盐为 300× 2 2+ 1 = 200 克。“损益法”其实是一种口算 法, 有的题运用损益法非常简捷。 4“特殊”代替“一般”, 逻辑推理错误 例如: 2000 年初赛试题(A ) 卷第 12 题, 有 8 级台 阶, 小明从下向上走, 若每次只能跨一级或两级, 他走 上去可有 种不同方法。 答案: 34。 分析: 先看一级、二级、三级台阶各有几种不同的 跨法 ③再画出三级台阶, 易发现有五种不同跨法, 若 四级台阶呢? 也不难发现有三种不同跨法, 将台阶级 数与对应的不同跨法排成下表, 就会有所发现。 台阶级数 1 2 3 4 5 … 8 不同跨法 1 2 3 5 8 … ? 规律已显现在眼前, 1, 2, 3 (= 2+ 1) , 5 (= 3+ 2) , 8 (= 5+ 3) , 13 (= 8+ 5) , 21= (13+ 8) , 34 (= 21+ 13) , 即为 1、2、3、4、5、6、7、8 级台阶的不同跨法, 所以 有8 级台阶, 每次跨一级或两级共有34种不同的方法。 笔者评:“分析”中所说的“规律”, 仅凭“3= 2+ 1, 5= 3+ 2, ”两个特例就得出一般情况, 即所谓“规律”, 是很不够的, 即使有更多的特例也只能说是个经验命 题或猜想命题, 这类命题, 在没有经过逻辑推论前是 不能作为论据的。所以“分析”中所得出的答案是否可 靠值得怀疑。因此, 提出用相间插空法来解。 不同的跨法分为五类: (一) 四次都跨两级走上去, 只有 1 种跨法; (二) 三次跨两级二次跨一级走上去, 为了方便这 里用一个“双”字表示一次跨两级, 用一个“单”字表示 一次跨一级, 这里又分两种情况: 这一类两种情况共有 4+ 6= 10 种跨法。 ·6· 萍乡高等专科学校学报 2009 年

第3期 李幼年:小学数学奥赛试题解再评析 。7. (三)二次跨两级四次跨一级走上去 双双单 单 ·双双4 单 双双 单 单 单 双双 效 单 单 双双 双 单 双 单 单 效 单 单 单单 什 单单 双 单 双 单单 双 双 单 双 ·单 单单 中 单单 双 单 双 15种跨法 (四)一次跨两级六次跨一级走上去 双 单 单 双 单单 单单 单 单 单 中 单单 单单 单单 效 单单 单单 单单单 单单 双 单 双 这一类共有7种跨法。 (五)全是跨一级的跨法走上去:显然只有1种跨 有出版社2004 法。综合以上五类共有不同的跨法。1+10+15+7+ 21 1=34种。 参考文献 债任编校王科) 【】蓝润,杨跃小学数学奥林匹克竞赛M】武汉:湖北教 On the Solution of Mathematics Olym piad Questions of Prmary School Li Younian (Pingx iang College,Pingxiang 337000.China) Abstract A fter po inting out and analyzing them istake and inadequate of the m athem aticsO lympiad question,this paper puts forward some new thoughts and ways which can fully reflect the am of O lympiad more directly. Key words O lympiad,analyzing process.ogical reasoning 1994-2009 China Academic Journal Electronie Publishing House.All rights reserved hup:/Awww.cnki.ne
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net (三) 二次跨两级四次跨一级走上去: 这一类共 5+ 10= 15 种跨法。 (四) 一次跨两级六次跨一级走上去: 这一类共有 7 种跨法。 (五) 全是跨一级的跨法走上去: 显然只有 1 种跨 法。综合以上五类共有不同的跨法。1+ 10+ 15+ 7+ 1= 34 种。 参 考 文 献 [1 ] 蓝涧, 杨跃. 小学数学奥林匹克竞赛[M ]. 武汉: 湖北教 育出版社, 2004. [2 ] 李幼年. 小学数学奥赛试题解评析[J ]. 萍乡高等专科学 校学报, 2008, 25 (3): 21~ 25. 〔责任编校: 王 科〕 On the Solution of M athematics O lym p iad Question s of Pr imary School L i Youn ian (Pingx iang Co llege, Pingx iang 337000, Ch ina) Abstract: A fter po in ting ou t and analyzing the m istake and inadequate of the m athem atics O lymp iad question, th is paper pu ts fo rw ard som e new though ts and w ays w h ich can fu lly reflect the aim of O lymp iad mo re directly. Key words: O lymp iad; analyzing p rocess; logical reason ing 第 3 期 李幼年: 小学数学奥赛试题解再评析 ·7·