
上讲提要 1.拉格朗日中值定理及其推论; 2洛比达法则: 3.单调性、极值
3 上讲提要 1.拉格朗日中值定理及其推论; 2.洛比达法则; 3.单调性、极值

第四节 导数的应用 三、函数的单调性和极值 3、最大值、最小值 函数f(x)在区间I上的全部函数 值中最大者(最小者),称为函数f(x)在I上的最大值(最 小值)。 求法 (1)f(x)在[a,b]上连续,先求出f(x)在[a,b]所有的驻点及导 数不存的点x,x2,…,xn,然后求出这些点及端点的函数值 f(),f(x),f(x2),…,f(xn),f(b),并比较,其最大者为最大 值,最小者为最小值。 (2)f(x)在[a,b]上单调,f(x)单调递增,最大值f(b),最小 值f(a);单调递减,最大值f(a),最小值f(b):
4 第四节 导数的应用 三、函数的单调性和极值 3、最大值、最小值 函数 f x( )在区间I上的全部函数 值中最大者(最小者),称为函数 f x( )在I上的最大值(最 小值)。 求法 (1) f x( )在[ , ] a b 上连续,先求出 f x( )在[ , ] a b 所有的驻点及导 数不存的点 1 2 , , , n x x x ,然后求出这些点及端点的函数值 1 2 ( ), ( ), ( ), , ( ), ( ) n f a f x f x f x f b ,并比较,其最大者为最大 值,最小者为最小值。 (2) f x( )在[ , ] a b 上单调,f x( )单调递增,最大值 f b( ),最小 值 f a( );单调递减,最大值 f a( ),最小值 f b( );

(3)f(x)在区间I上可导,且只有一个驻点x,且x是f(x) 的极值点,则f(x)为极大值时,就是I上的最大值; f(x)为极小值时,就是I上的最小值。 例1求函数f(x)=(x+4)(x-1)2在[-2,2]上的最大 值、最小值。 f)=6-+x+4Xx-)- 解 (x+1) x-1 令f'(x)=0,得驻点x=-1;x=1时,f'(x)不存在。 f(-2)=239≈4.16 f(-1)=3/4≈4.76, f(1)=0 f(2)=6 比较上述函数值,得f(x)的最大值为f(2)=6,最5
5 (3) f x( )在区间I上可导,且只有一个驻点 0 x ,且 0 x 是 f x( ) 的极值点,则 0 f x( )为极大值时,就是I 上的最大值; 0 f x( )为极小值时,就是I上的最小值。 例 1 求函数 3 2 f x x x ( ) ( 4) ( 1) = + − 在[ 2,2] − 上的最大 值、最小值。 解 1 3 2 3 3 2 5( 1) ( ) ( 1) ( 4)( 1) 3 3 1 x f x x x x x − + = − + + − = − 令 f x ( ) 0 = ,得驻点x = −1;x = 1时, f x ( )不存在。 3 f ( 2) 2 9 4.16 − = 3 f ( 1) 3 4 4.76 − = , f (1) 0 = f (2) 6 = 比较上述函数值,得 f x( )的最大值为 f (2) 6 = ,最

小值为f(①)=0。 例2.求f(x)=x-sinx在[0,2π]上的最大值,最小值 解f'(x)=1-cosx>0,x∈(0,2π) f(x)在[0,2π]上单调递增, 所以f(x)在[0,2π]上的最大值f(2π)=2π;最小值 f(0)=0。 例3.肌肉注射或皮下注射药物后,血中的药物浓度可表 为 A C= (eo-eo:) 02-01 其中A、o1、02是大于零的常数,且o2>o1,问时间t为 何值时,药物浓度为最大,最大浓度为多少? 6
6 小值为 f (1) 0 = 。 例2.求 f x x x ( ) sin = − 在[0,2 ] 上的最大值,最小值 解 f x co x ( ) 1 s 0 = − ,x(0,2 ) f x( )在[0,2 ] 上单调递增, 所 以 f x( ) 在[0,2 ] 上的最大值 f (2 ) 2 = ;最小值 f (0) 0 = 。 例3.肌肉注射或皮下注射药物后,血中的药物浓度可表 为 1 2 2 1 ( ) A t t C e e − − = − − 其 中A、1、 2是大于零的常数,且 2 1 ,问时 间t为 何值时,药物浓度为最大,最大浓度为多少?

解 A C= (o2e1-01ea4) 02-01 令C'=0,可得1=lno,-lno 02-01 A C”= (o1e-022e) 02-01 。A 1- 2:) 2 1 1(Ino2-Ino1) cwoa 02-01 <0 01 故1=no?-lno时,C取极大值为4 02-01 02-01 02 7
7 解 2 1 2 1 2 1 ( ) A t t C e e − − = − − 令C = 0,可得 2 1 2 1 ln ln t − = − 1 2 1 1 2 2 2 1 2 2 1 2 2 2 ( ) 1 2 2 1 1 ( ) 1 t t t t A C e e A e e − − − − = − − = − − 1 2 1 2 1 (ln ln ) 2 1 1 2 1 ln ln C A e 0 − − − − = − − 故 2 1 2 1 ln ln t − = − 时,C取极大值为 1 2 1 1 2 2 A −

由于C在[0,+o)上只有一个极大值点,且t→+∞ 时,c→0。 所以1=-na时,C达到最大值 02-01 01 02-01 即当时间t= lno2-lnC1时,血药浓 02-01 01 01 02-1 度为最大,其最大浓度为口 2 02 四、函数曲线的凹凸性和拐点 1.概念 定义2-4设函数y=f(x)在[a,b]上连续,如果对于 [a,b]上的任意两点x,x2,有 8
8 由 于C 在[0, ) + 上只有一个极大值点,且t → + 时,c → 0。 所 以 2 1 2 1 ln ln t − = − 时 , C 达 到 最 大 值 1 2 1 1 max 2 2 A C − = 。即当时间 2 1 2 1 ln ln t − = − 时,血药浓 度为最大,其最大浓度为 1 2 1 1 2 2 A − 。 四、函数曲线的凹凸性和拐点 1.概念 定 义 2-4 设函数 y f x = ( )在[ , ] a b 上连续,如果对于 [ , ] a b 上的任意两点 1 2 x x, ,有
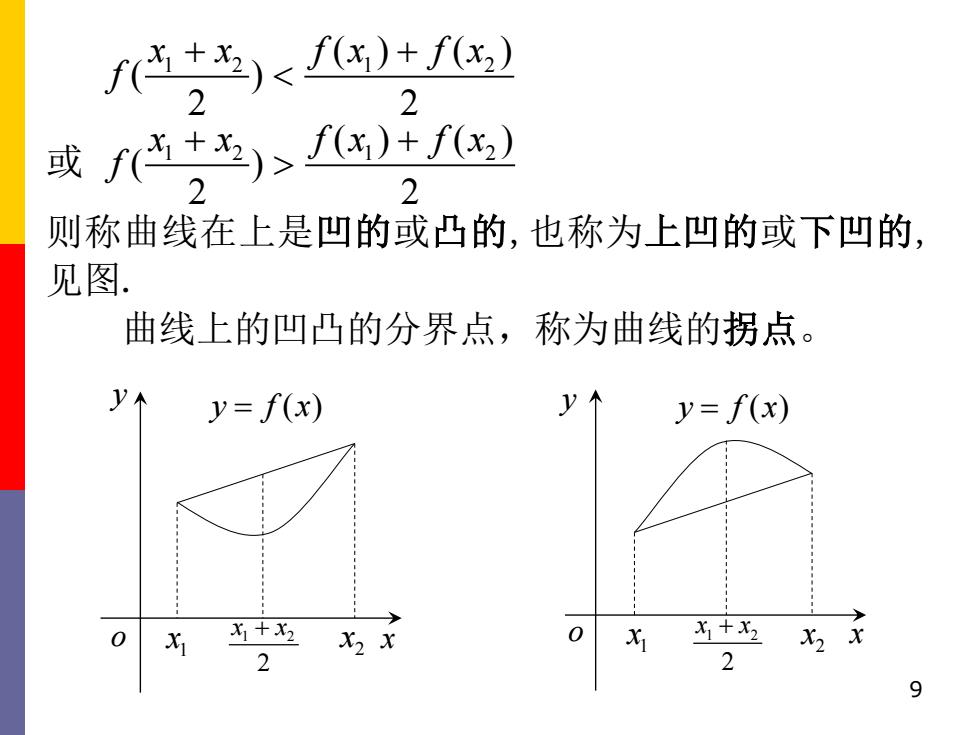
f)fx)+f) 2 则称曲线在上是凹的或凸的,也称为上凹的或下凹的, 见图. 曲线上的凹凸的分界点,称为曲线的拐点。 y=f(x) y=f(x) X 为十 X2 X X+x2 X2 x 2 2 9
9 1 2 1 2 ( ) ( ) ( ) 2 2 x x f x f x f + + 或 1 2 1 2 ( ) ( ) ( ) 2 2 x x f x f x f + + 则称曲线在上是凹 的或凸 的,也称为上凹的或下凹的, 见图. 曲线上的凹凸的分界点,称为曲线的拐点。 1 2 2 x x + y o x 1 x 2 x y f x = ( ) y o x 1 x 2 1 2 x 2 x x + y f x = ( )

2.凹凸性的判别法 定理2-10设函数y=f(x)在(a,b)内具有二阶导数f"(x), 则有 ①若对任意x∈(a,b),有f"(x)>0,则曲线f(x)在(a,b) 内是凹的: ②若对任意x∈(a,b),有f"(x)<0,则曲线f(x)在 (a,b)内是凸的: 例1.判别曲线f(x)=lnx的凹凸性。 解 函数f(x)=lnx定义域为(0,+o), /)-子)-<0. 10
10 2.凹凸性的判别法 定理2-10 设函数y f x = ( )在( , ) a b 内具有二阶导数 f x ( ), 则有 ①若对任意x a b ( , ),有 f x ( ) 0 ,则曲线 f x( )在( , ) a b 内是凹的; ②若对任意 x a b ( , ),有 f x ( ) 0 ,则曲线 f x( )在 ( , ) a b 内是凸的; 例 1.判别曲线 f x x ( ) ln = 的凹凸性。 解 函数 f x x ( ) ln = 定义域为(0, ) + , 1 f x( ) x = , 2 1 f x( ) 0 x = −

例2判别曲线f(x)=3x-x3的凹凸性。 解函数f(x)的定义域为(-o,+oo) f'(x)=3-3x2 f"(x)=-6x 在(-0,0)上,f"(x)>0,则此曲线在(-0,0)上是凹的; 在(0,+o)上,f"(x)0,由曲线f(x)在(-0,0)上是凹的, 在(0,+o)上,"(x)<0,则曲线f(x)在(0,+o)上是凸的, 又f(0)=0所以(0,0)点为曲线拐点。 11
11 例2 判别曲线 3 f x x x ( ) 3 = − 的凹凸性。 解 函数 f x( )的定义域为( , ) − + 2 f x x ( ) 3 3 = − f x x ( ) 6 = − 在( ,0) − 上, f x ( ) 0 ,则此曲线在( ,0) − 上是凹的; 在(0, ) + 上, f x ( ) 0 ,则此曲线在(0, ) + 上是凸的。 例3.判别曲线 3 f x x ( ) = 的凹凸性,并求拐点。 解 函数 f x( )的定义域为( , ) − + , 在( ,0) − 上, f x ( ) 0 ,由曲线 f x( )在( ,0) − 上是凹的, 在(0, ) + 上, f x ( ) 0 ,则曲线 f x( )在(0, ) + 上是凸的, 又 f (0) 0 = ,所以(0,0)点为曲线拐点

3.判别凹凸性求拐点方法 设曲线y=f(x)除有限个点外二阶导数存在 ①先求函数y=f(x)的定义域; ②在定义域内求f"(x)等于零的点和不存在的点 X13X22,Xn; ③用x1,x2,…,x将定义域分成若干个区间,每个区间 上二阶导数符号恒定,从而判别各个区间上曲线的凹 凸性,并可得(x,f(x》,i=1,2,…,n是否为拐点。 4讨论曲线f)-x+(x-的凸惟及拐点。 解函数f(x)的定义域为(-oo,+o), 12
12 3.判别凹凸性求拐点方法 设曲线y f x = ( )除有限个点外二阶导数存在 ①先求函数y f x = ( )的定义域; ②在定义域内求 f x ( )等于零的点和不存在的点 1 2 , , , n x x x ; ③用 1 2 , , , n x x x 将定义域分成若干个区间,每个区间 上二阶导数符号恒定, 从而判别各个区间上曲线的凹 凸性,并可得( , ( )) i i x f x ,i n =1,2, , 是否为拐点。 例4.讨论曲线 5 2 3 5 ( ) ( 1) 9 f x x x = + − 的凹凸性及拐点。 解 函数 f x( )的定义域为( , ) − +