
上讲提要 1.函数的概念、性质 2.极限、无穷小、无穷大的概念及有关性质
上 讲 提 要 1. 函数的概念、性质 2. 极限、无穷小、无穷大的概念及有关性质

第二节, 极限 三、极限的四则运算 定理 若1imf(x)=A,Iimg(x)=B,则 (I)lim[f(x)±g(x)】=limf(x)±limg(x)=A±B (2)lim[f(x)g(x)]=lim f(x)limg(x)=4B 特别limlef(x】=climf(x)=cA,c∈R limf(x)]”=[limf(x)'=A",n∈N (3)limf(x)=limf()4 (B≠0) g(x)limg(x)B
第二节 极限 三、极限的四则运算 定理 若lim ( ) f x A = ,lim ( ) g x B = ,则 ⑴ lim[ ( ) ( )] lim ( ) lim ( ) f x g x f x g x A B = = ⑵ lim[ ( ) ( )] lim ( )lim ( ) f x g x f x g x AB = = 特别 lim[ ( )] lim ( ) cf x c f x cA = = ,c R lim[ ( )] [lim ( )] n n n f x f x A = = ,n N ⑶ ( ) lim ( ) lim ( 0) ( ) lim ( ) f x f x A B g x g x B = =

证明 (1) 因为1imf(x)=A,limg(x)=B 所以 f(x)=A+a,8(x)=B+B 其中 lima=0,lim B=0 f(x)±8(x)=(A+)±(B+B)=(A±B)+(C±B) 而 lim(a±B)=0 故 lim[f(x)±g(x)]=A±B (2)(3)同理可证 结论(1)limC=C,(c为常数) (2) limx=xo,limx”=x,” x→x0 X→x0 1 (3) lim=0,(a>0) x→0X (4) limq=0,(1qk1) x→+o0
证明 (1) 因为lim ( ) f x A = ,lim ( ) g x B = 所以 f x A ( ) = + ,g x B ( ) = + 其中 lim 0 = ,lim 0 = f x g x A B A B ( ) ( ) ( ) ( ) ( ) ( ) = + + = + 而 lim( ) 0 = 故 lim[ ( ) ( )] f x g x A B = (2)(3)同理可证 结 论 (1) limC C= ,(C为常数) (2) 0 0 lim x x x x → = , 0 0 lim n n x x x x → = (3) 1 lim 0 x x → = ,( 0) (4) lim 0 x x q →+ = ,(| | 1 q )

例1.求1imx-I 2x2-1 x-1 lim(x-1) limx-liml 解 x→2 →2 2-11 lim- x→2 x2-1 lim(x2-1)lim x2-lim1 22-13 x→2 X→2 X→2 例2.求1im x-1 1x2-1 解 x-1 lim- x-1 =lim =lim xx2-1 1(x-1)(x+1) x+1) 例3.求im 1+x-2 x→3 x-3 解 +x-2=lim (W1+x-2)W1+x+2) x-3 (x-3)(W1+x+2) x-3 1 lim- lim x3(x-3(√1+x+2)x1+x+24
例1.求 2 2 1 lim x 1 x → x − − 解 2 2 2 2 2 2 2 2 2 2 lim( 1) lim lim1 1 lim 1 lim( 1) lim lim1 x x x x x x x x x x x x x → → → → → → → − − − = = − − − 2 2 1 1 2 1 3 − = = − 例2.求 2 1 1 lim x 1 x → x − − 解 2 1 1 1 1 1 1 1 lim lim lim x x x 1 ( 1)( 1) 1 2 x x → → → x x x x − − = = = − − + + 例3.求 3 1 2 lim x 3 x → x + − − 解 3 3 1 2 ( 1 2)( 1 2) lim lim 3 ( 3)( 1 2) x x x x x → → x x x + − + − + + = − − + + 3 3 3 1 1 lim lim x x ( 3)( 1 2) 1 2 4 x → → x x x − = = = − + + + +
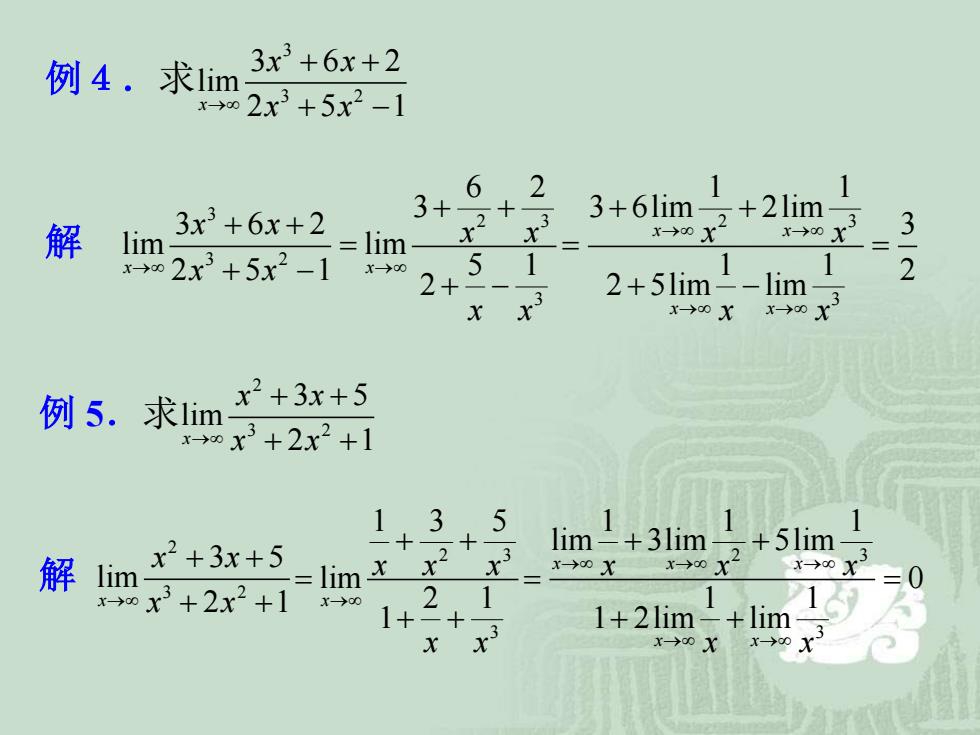
例4.求lim 3x3+6x+2 02x3+5x2-1 6 2 1 3+ 3+6lim+2lim3 解 3x3+6x+2 3 lim 2lim2大】 x→0X r-→0X x02x3+5x2-1x→ 2+5 1 1 2+5lim--lim 2 x x3 x→0X x→0X1 例5.求1im x2+3x+5 xx3+2x2+1 1,3 1 一十 lim+3lim+5lim 解 lim x2+3x+5 1:xx2 x→0X x-→00X1 x→0X =0 x0x3+2x2+1 21 1人 1+-+ 1+2lim+lim x-→0X x-→0X
例4.求 3 3 2 3 6 2 lim x 2 5 1 x x → x x + + + − 解 3 2 3 3 2 3 6 2 3 3 6 2 lim lim 2 5 1 5 1 2 x x x x x x x x x x → → + + + + = + − + − 2 3 3 1 1 3 6lim 2lim 3 1 1 2 2 5lim lim x x x x x x x x → → → → + + = = + − 例 5.求 2 3 2 3 5 lim x 2 1 x x → x x + + + + 解 2 3 2 3 5 lim x 2 1 x x → x x + + + + 2 3 3 1 3 5 lim 2 1 1 x x x x x x → + + = + + 2 3 3 1 1 1 lim 3lim 5lim 0 1 1 1 2lim lim x x x x x x x x x x → → → → → + + = = + +

例6. 求im 2+2x+5 x→00 x+3 1.3 一十 解 因为 x+3 lim- -=0 →0x2+2x+5 lim-x x? x→0 .5 1+ 十 所以 x2+2x+5 lim =00 x→0 x+3 0 nm 其中,a,b≠0
例 6.求 2 2 5 lim x 3 x x → x + + + 解 因为 2 3 lim x 2 5 x → x x + + + 2 2 1 3 lim 0 2 5 1 x x x x x → + = = + + 所以 2 2 5 lim x 3 x x → x + + = + 结 论 1 0 1 1 0 1 lim n n n m m x m a x a x a b x b x b − → − + + + = + + + 0 0 0 n m a n m b n m = 其中, 0 0 a b, 0

例7.求limx(Wx2+2-x) 解1imxN2+2-)=1mV+2-x+2+ x)+0 √x2+2+x 2x 2 lim- -lim -=1 x+0√x2+2+ x→+0 2 ++ 例8.求1im 解】 3 x2-x-2 lim- x-2 x(x+1(x2-x+0,1x2-x+1 lim x-lim 2 x→-1 x→-1 -1-2为 lim x2-limx+lim 1 (-1)2-(-1)+1 x→-1 x→>-1 x→-1
例 7.求 2 lim ( 2 ) x x x x →+ + − 解 2 lim ( 2 ) x x x x →+ + − 2 2 2 ( 2 )( 2 ) lim 2 x x x x x x x x →+ + − + + = + + 2 2 2 2 lim lim 1 2 2 1 1 x x x x x x →+ →+ = = = + + + + 例 8.求 3 1 1 3 lim x→− x x 1 1 − + + 解 3 1 1 3 lim x→− x x 1 1 − + + 2 2 1 2 lim ( 1)( 1) x x x →− x x x − − = + − + 2 1 2 lim x 1 x →− x x − = − + 1 1 2 2 1 1 1 lim lim 2 1 2 1 lim lim lim1 ( 1) ( 1) 1 x x x x x x x x →− →− →− →− →− − − − = = = − − + − − − +

x2-1 例9.f(x)=了x-1 x1f x-1 x-→1 f(1+0)=lim(x2+1)=2 故 f(1-0)=f(1+0)=2 所以 lim f(x)=2
例 9. 2 2 1 1 ( ) 1 1 1 x x f x x x x − = − + ,求 1 lim ( ) x f x → 解 2 1 1 (1 0) lim x 1 x f x → − − − = − 1 1 ( 1)( 1) lim lim( 1) 2 x x 1 x x x x → → − − − + = = + = − 2 1 (1 0) lim( 1) 2 x f x → + + = + = 故 f f (1 0) (1 0) 2 − = + = 所以 1 lim ( ) 2 x f x → =

四.两个重要的极限 1. lim sinx =1 x→0 X 例1.求1im tanx x→0 解 tan x inx lim lim( 1 )=lim sin x.limc 一=1 x→0 x x0 COSX 1 例2.求limxsin X→00 解 令1=1,x→o时,t→0,于是 1 sin- 1 limxsin=lim- x=lim si 1=1 x→0 Xx-→∞ 1 t→0 x
四.两个重要的极限 1. 0 sin lim 1 x x → x = 例1.求 0 tan lim x x → x 解 0 0 0 0 tan sin 1 sin 1 lim lim( ) lim lim 1 cos cos x x x x x x x → → → → x x x x x = = = 例2.求 1 lim sin x x → x 解 令 1 t x = ,x →时,t → 0,于是 0 1 sin 1 sin lim sin lim lim 1 x x t 1 t x x x t x → → → = = =
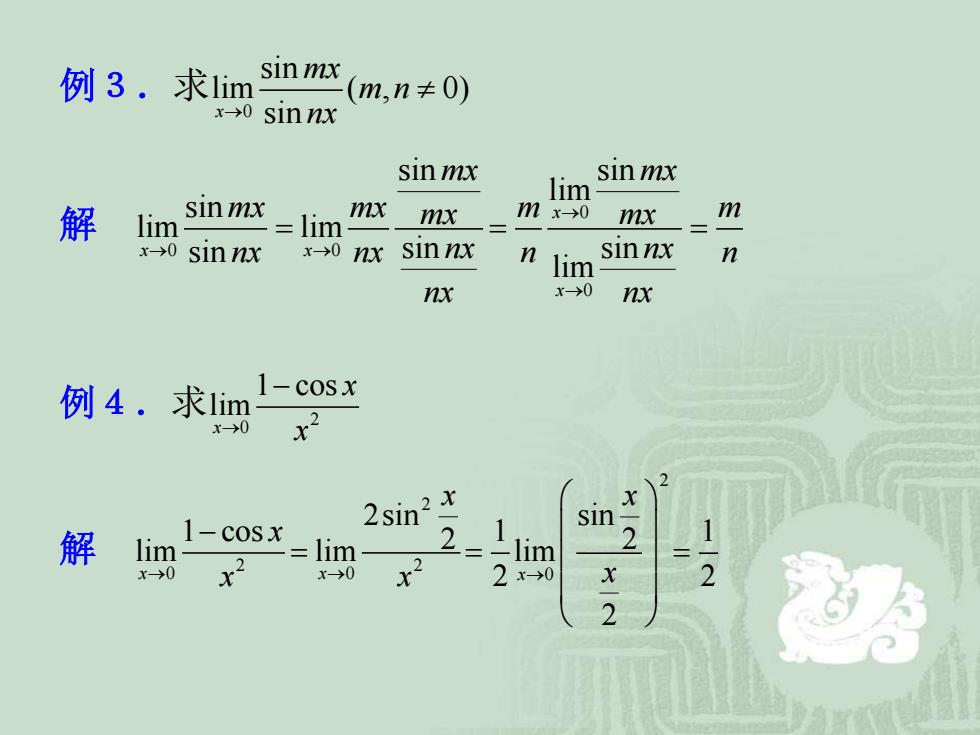
例3.求1im sin mx(m,n≠0) x-→0 sinnx sinmx lim sinmx 解 lim sinmx =lim mx= m x0 mx m x→0 sin nx x0 nx sinnx n lim sinnx n nx x→0 nx 例4.求1im 1-cosx x→>0 2 2sin2 解 1-cosx 1 sin- 1 lim lim 21 lim 2 x-→0 x→0 x0 X -2 2
例3.求 0 sin lim ( , 0) x sin mx m n → nx 解 0 0 sin sin lim lim x x sin sin mx mx mx mx nx nx nx nx → → = 0 0 sin lim sin lim x x mx m m mx n n nx nx → → = = 例4.求 2 0 1 cos lim x x → x − 解 2 0 1 cos lim x x → x − 2 2 0 2sin 2 lim x x → x = 2 0 sin 1 2 lim 2 2 x x → x = 1 2 =