
一元函数微分学小结 一、 导数 概念、几何意义、 公式、求导法则 二、微分 概念、几何意义、可导与可微、 一阶微分形式的不变性
3 一元函数微分学小结 一、导数 概念、几何意义、 公式、求导法则 二、微分 概念、几何意义、可导与可微、 一阶微分形式的不变性
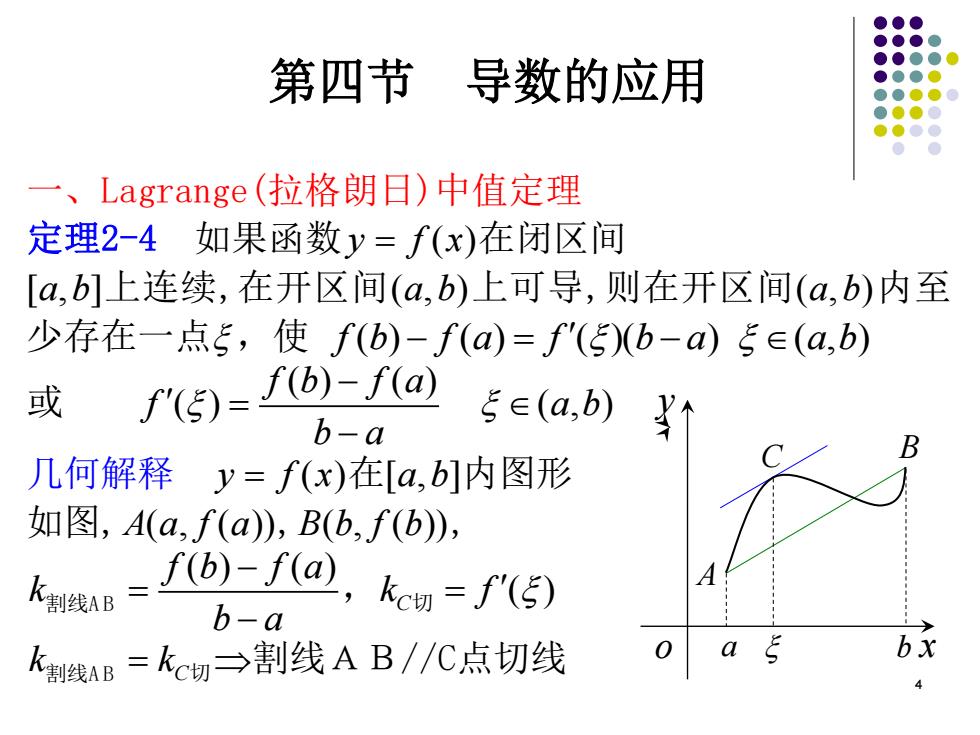
第四节 导数的应用 一、Lagrange(拉格朗日)中值定理 定理2-4如果函数y=f(x)在闭区间 [a,b]上连续,在开区间(a,b)上可导,则在开区间(a,b)内至 少存在一点5,使f(b)-f(a)=f'(5)b-a5∈(a,b) 或 f(5)=f6)-fa b-a 5∈(a,b) 21 B 几何解释y=f(x)在[a,b]内图形 如图,A(a,f(a),B(b,f(b), k(b)-f(a),kes=f() b-a k制线AB=kc切→割线AB/C点切线 a bx
4 第四节 导数的应用 一、Lagrange(拉格朗日)中值定理 定理2-4 如果函数y f x = ( )在闭区间 [ , ] a b 上连续,在开区间( , ) a b 上可导,则在开区间( , ) a b 内 至 少存在一点,使 f b f a f b a a b ( ) ( ) ( )( ) ( , ) − = − 或 ( ) ( ) ( ) ( , ) f b f a f a b b a − = − 几何解释 y f x = ( )在[ , ] a b 内图形 如图,A a f a ( , ( )),B b f b ( , ( )), f b f a ( ) ( ) k b a − = − 割线A B , ( ) C k f 切 = C k k 割线A B = 切 割线AB//C点切线 y o x A C B a b

●●● 推论1x∈(a,b),若有f'(x)=0,则f(x)=c(c为常数3 证明、 x<x2∈(a,b),则f(x)在[x,x2]上可导 故f(x)在[x,x2]上连续,在(x,x2)可导 于是,由Lagrange中值定理。有 f(x2)-f(x)=f"(5)x2-x),5∈(xx2) 由f'(5)=0,则f(x2)-f(x)=0 即 f(x)=f(x2) 所以 f(x)=c 推论2、 x∈(a,b),若有f'(x)=g'(x),则f(x)=g(x)+c (c为常数) 证明 令 F(x)=f(x)-8(x) 则 F'(x)=f'(x)-g'(x)=0 由推论1 F(x)=c,即 f(x)=8(x)+c
5 推论1 x a b ( , ),若有 f x ( ) 0 = ,则 f x c ( ) = (c为常数)。 证明 1 2 x x a b ( , ),则 f x( )在 1 2 [ , ] x x 上可导 故 f x( )在 1 2 [ , ] x x 上连续,在 1 2 ( , ) x x 可导 于是,由Lagrange中值定理。有 2 1 2 1 1, 2 f x f x f x x x x ( ) ( ) ( )( ), ( ) − = − 由 f ( ) 0 = ,则 2 1 f x f x ( ) ( ) 0 − = 即 1 2 f x f x ( ) ( ) = 所以 f x c ( ) = 推论2 x a b ( , ),若有 f x g x ( ) ( ) = ,则 f x g x c ( ) ( ) = + (c为常数) 证明 令 F x f x g x ( ) ( ) ( ) = − 则 F x f x g x ( ) ( ) ( ) 0 = − = 由推论1 F x c ( ) = ,即 f x g x c ( ) ( ) = +

例1.验证f(x)=lnx在[L,e]上Lagrange中值定理的正确件 证明 因为f(x)=lnx为基本的初等函数,其定义域为 (0,+o0),故f(x)在(0,+0)上连续, 从而在L,e上连续,f(x)=】,故fx)在Le)上可导, f(e)-f)=f'(5)e-1) 即 e-=1枚=e-1ee. 所以,f(x)=lnx在[l,e]上Lagrange中值定理是正确 的
6 例 1.验证 f x x ( ) ln = 在[1, ] e 上 Lagrange 中值定理的正确性。 证 明 因 为 f x x ( ) ln = 为基本的初等函数,其定义域为 (0, ) + ,故 f x( )在(0, ) + 上连续, 从而在[1, ] e 上连续, 1 f x( ) x = ,故 f x( )在(1, ) e 上可导, f e f f e ( ) (1) ( )( 1) − = − 即 1 ( 1) 1 e − = ,故 = − e e 1 (1, ), 所以, f x x ( ) ln = 在[1, ] e 上 Lagrange 中值定理是正确 的

例2.试证x>0时,x0时,,x<nl+)<x 1+x
7 例 2.试证 x 0时, ln(1 ) 1 x x x x + + 证明 设 f x x ( ) ln(1 ) = + , 因为 f x( )为初等函数,其定义域为 ( 1, ) − + ,故 f x( )在[0, ] x 上连续。 又 1 ( ) 1 f x x = + ,故 f x( )在(0, x)上可导,则 f x f f x x ( ) (0) ( )( 0), (0, ) − = − 即 1 ln(1 ) 1 x x + = + , 所以 1 1 1 0 x x x x x = + + + 从而,x 0时, ln(1 ) 1 x x x x + +

例3.试证明x≠0时, 1π arctanx arctan-= x 2 证明设f(x)=arctanx+arctan X x≠0时,f'(x)= 1+ 由推论1,x≠0时,f(x)=c(c为常数) 取x=1,f0)=+==c 442
8 例 3.试证明x 0时, 1 arctan arctan 2 x x + = 。 证明 设 1 f x x ( ) arctan arctan x = + x 0时, 2 2 2 1 1 1 ( ) ( ) 1 1 1 f x x x x = + − + + 2 2 1 1 0 1 1 x x =−= + + 由推论 1,x 0时, f x c ( ) = (c为常数) 取 x = 1, (1) 4 4 2 f c = + = =

二、L'Hospital(洛必达)法则 若当x→x,(或x→士0)时极 1imfx)=limg)=0或o,那么极限1im叫做不定 8(x) 式(未定式),分别记作9或2。还有00,,0,0°,0- 000 等五种类型不定式。 定理2-5若函数f(x)与g(x)满足下列条件: (1)当x→x(或x→∞)时,f(x)与g(x)都趋于0或0; (2)在U(x)(或x>N)内,f'(x),g'(x)都存在,且g'(x)≠0; (3)lim '(x存在或无穷大: g'(x) 则 lim f(x) lim f'(x) 8(x) g'(x)
9 二、L′Hospital(洛必达)法则 若 当 0 x x → ( 或 x → ) 时 极 限 lim ( ) lim ( ) 0 f x g x = = 或,那么极限 ( ) lim ( ) f x g x 叫做不定 式(未定式), 分别记作0 0 或 。还有 0 0 0 ,1 ,0 , , − 等五种类型不定式。 定理2-5 若函数 f x( )与g x( )满足下列条件: (1)当 0 x x → (或x → )时, f x( )与g x( )都趋于0或; (2)在 0 U x( )(或| | x N )内, f x ( ),g x ( )都存在,且g x ( ) 0 ; (3) ( ) lim ( ) f x g x 存在或无穷大; 则 ( ) ( ) lim lim ( ) ( ) f x f x g x g x =

使用L'Hospital法则时,若1m)仍为 (或 g'(x) 0 不定式,而极限mC四存在或无穷大, "(x) 则 lim f(x) =lim=lim f() 8(x) g'(x) g"(x) 一般情况,若 lim f(x)lim= (x) g'(x) g(n-D(x) 皆是 (或”) 0 不定式,而极限1inm(y 存在或无穷大, 00 g(x) 则mf)=1imf-lim-=lim 8x) 8'(x) g"(x) g(x) 10
10 使用LHospital法则时,若 ( ) lim ( ) f x g x 仍为0 0 (或 ) 不定式,而极限 ( ) lim ( ) f x g x 存在或无穷大, 则 ( ) ( ) lim lim ( ) ( ) f x f x g x g x = ( ) lim ( ) f x g x = 一般情况,若 ( 1) ( 1) ( ) ( ) ( ) lim ,lim , ,lim ( ) ( ) ( ) n n f x f x f x g x g x g x − − 皆是 0 0 (或 )不定式,而极限 ( ) ( ) ( ) lim ( ) n n f x g x 存在或无穷大, ( ) ( ) ( ) ( ) ( ) ( ) lim lim lim lim ( ) ( ) ( ) ( ) n n f x f x f x f x g x g x g x g x = = = = 则

例1.求lim x-sinx x→0 inx 解 x-sinx 1-cosx=lim- lim 比J =lim x→0 x-0 3x2 x→0 6x lim cosx 1 x-→0 6 6 x3-3x+2 例2.求lim 1x3-x2-X+1 解 x3-3x+2 3x2-3 6x 3 --x+1四3x2-2x-196x-22 =lim- =lim- 11
11 例1.求 3 0 sin lim x x x → x − 解 3 2 0 0 sin 1 cos lim lim x x 3 x x x → → x x − − = 0 sin lim x 6 x → x = 0 cos 1 lim x 6 6 x → = = 例2.求 3 3 2 1 3 2 lim x 1 x x → x x x − + − − + 解 3 2 3 2 2 1 1 1 3 2 3 3 6 3 lim lim lim x x x 1 3 2 1 6 2 2 x x x x → → → x x x x x x − + − = = = − − + − − −

Inx 例3.求lim (a>0) 术-→+0Xa 1 Inx 1 解 lim 气=maa-寸m -=0 x>xa 例4.求1imX” oe(n∈N,>0) x" lim nxm-1 *e在slim (n-1)x"-2 解 xrlim xto 12eir n! =…=lim +∞"ei 0 12
12 例3.求 ln lim ( 0) a x x a →+ x 解 1 1 ln 1 lim lim lim 0 a a a x x x x x x ax ax →+ →+ →+ − = = = 例4.求 lim n x x x e →+ (n N , 0) 解 1 2 2 ( 1) lim lim lim ! lim 0 n n n x x x x x x n x x x nx n n x e e e n e − − →+ →+ →+ →+ − = = = = =