
第三章一元函数积分学 第一节不定积分 一、不定积分的概念 (引例 例1.己知自由落体运动在t时刻的速度v=ft)=gt,当 t=0时,物体所在的位置s=0,求物体下落的路 程s与下落时间t的关系? 解 设所求的路程s与下落时间t的关系为s=F(t) 于是 s'=F'(t)=v=f(t)=8t 3
3 第三章 一元函数积分学 第一节 不定积分 一、不定积分的概念 ㈠引例 例1. 已知自由落体运动在t时刻的速度v f t gt = = ( ) ,当 t = 0时,物体所在的位置s = 0,求物体下落的路 程s与下落时间t的关系? 解 设所求的路程s与下落时间t的关系为s F t = ( ) 于是 s F t v f t gt ' '( ) ( ) = = = =

显然 5=F(t)= 2872+c 将s(0)=0代入得 c=0 故所求函数 s=F0=28r 例2.设某曲线上任意一点(x,y)处的切线斜率 k=f(x)=2x,求曲线方程。 解设所求的曲线方程y=F(x) 于是(x,y)点处的切线斜率为y'=F'(x)=f(x)=2x 显然 y=x2+c F'(x)=fx)台Fx)
4 显然 1 2 ( ) 2 s F t gt c = = + 将s(0) 0 = 代入得 c = 0 故所求函数 1 2 ( ) 2 s F t gt = = 例 2. 设某曲线上任意一点 ( , ) x y 处的切线斜率 k f x x = = ( ) 2 ,求曲线方程。 解 设所求的曲线方程y F x = ( ) 于是( , ) x y 点处的切线斜率为 y F x f x x ' '( ) ( ) 2 = = = 显然 2 y x c = + F x f x F x '( ) ( ) ( ) =

白概念 定义3-1 若在区间I上F'(x)=f(x),则称F(x)为f(x)在区 间1上的一个原函数。 F0-方号+c的为f0=g的原函数: F(x)=x2,x2+1,x2+c均为f(x)=2x的原函数。 结论1若函数f(x)在区间1上连续,那么在区间I上f(x)存 在原函数,即在区间1上存在可导函数F(x),使 F'(x)=f(x),x∈I 5
5 ㈡概念 定义 3-1 若在区间I上F x f x '( ) ( ) = ,则称F x( )为 f x( )在区 间I上的一个原函数。 1 1 2 2 ( ) , 2 2 F t gt gt c = + 均为 f t gt ( ) = 的原函数; 2 2 2 F x x x x c ( ) , 1, = + + 均为 f x x ( ) 2 = 的原函数。 结论 1 若函数 f x( )在区间I上连续,那么在区间I上 f x( )存 在原函数,即在区间I上存在可导函数F x( ),使 F x f x x I '( ) ( ), =

结论2若函数F(x)为f(x)在区间I上的一个原函数, 则 F(x)+c (c为任意常数) 也是f(x)在区间I上的原函数,且f(x)在区间的每一 个原函数都可表示成F(x)+c的形式。 证因为F(x)为f(x)的一个原函数,则F'(x)=f(x)。 (F(x)+c)'=F'(x)=f(x)(c任意常数) 因此,F(x)+c亦为f(x)的一个原函数。 设G(x)为f(x)的任一原函数,则G'(x)=f(x)。 6
6 结论 2 若函数F x( )为 f x( )在区间I 上的一个原函数, 则 F x c ( ) + (c为任意常数) 也 是 f x( )在区间I 上的原函数,且 f x( )在区间I 的每一 个原函数都可表示成F x c ( ) + 的形式。 证 因为F x( )为 f x( )的一个原函数,则F x f x '( ) ( ) = 。 ( ( ) )' '( ) ( ) F x c F x f x + = = (c任意常数) 因此,F x c ( ) + 亦为 f x( )的一个原函数。 设G x( )为 f x( )的任一原函数,则G x f x '( ) ( ) =

[G(x)-F(x]'=G'(x)-F'(x)=f(x)-f(x)=0 由Lagrange定理推论 G(x)-F(x)=c 即 G(x)=F(x)+c 定义3-2函数f(x)的全体原函数称为f(x)的不定积分, 又称为f(x)的原函数族,记作f(x)dx。 其中""为积分号,f(x)为被积函数,fx)为被积 表达式,x为积分变量。 若F'(x)=f(x),则f(x)d=F(x)+c。 7
7 [ ( ) ( )]' '( ) '( ) ( ) ( ) 0 G x F x G x F x f x f x − = − = − = 由Lagrange定理推论 G x F x c ( ) ( ) − = 即 G x F x c ( ) ( ) = + 定义 3-2 函数 f x( )的全体原函数称为 f x( )的不定积分, 又称为 f x( )的原函数族,记作 f x dx ( ) 。 其中" " 为积分号, f x( )为被积函数, f x dx ( ) 为被积 表达式,x为积分变量。 若F x f x '( ) ( ) = ,则 f x dx F x c ( ) ( ) = +
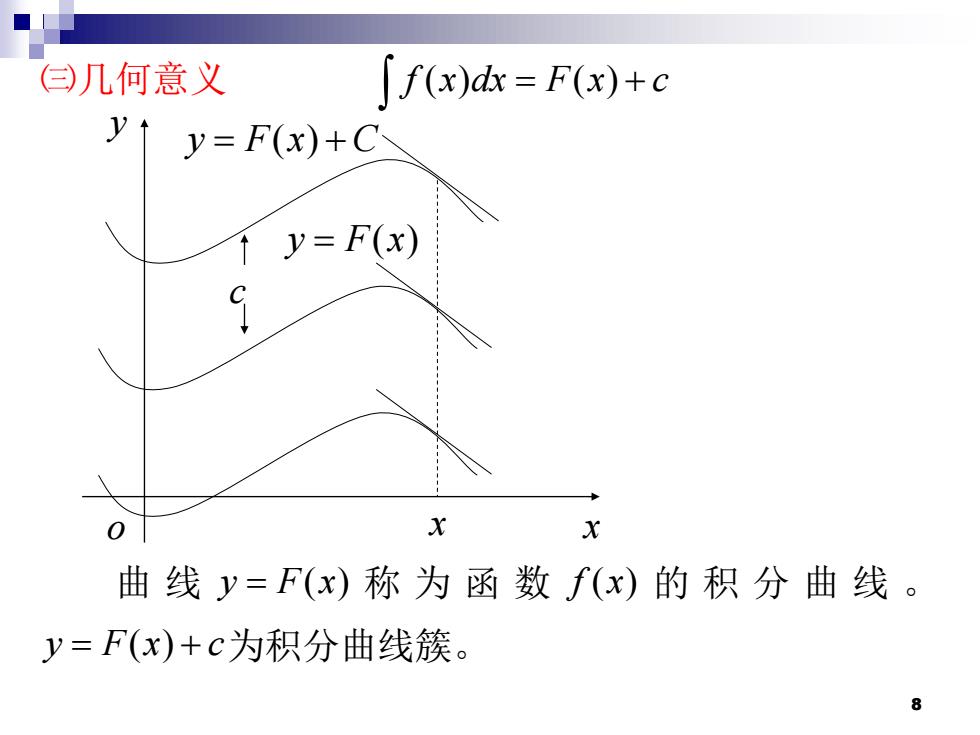
白)几何意义 「f(x)d=F(x)+c y↑ y=F(x)+C ↑y=F(x) X 曲线y=F(x)称为函数f(x)的积分曲线。 y=F(x)+c为积分曲线簇。 8
8 ㈢几何意义 f x dx F x c ( ) ( ) = + 曲 线 y F x = ( ) 称 为 函 数 f x( ) 的 积 分 曲 线 。 y F x c = + ( ) 为积分曲线簇。 y o x y F x C = + ( ) y F x = ( ) c x

例1.求sinxd。 解 因为 (-cosx)'=sinx 所以 [sinxdx=-cosx+c 例2.求经过(1,3)点,且其任意一点(x,y)处的 切线的斜率为3x2的曲线方程。 解设曲线方程y=F(x),则F'(x)=3x2 因为 (x3)'=3x2 所以F(x)=「3x2d=x3+c 得曲线族y=x3+c 将x=1,y=3代入得C=2。故所求曲线为y=x3+2。 9
9 例1. 求 sin xdx 。 解 因为 ( cos )' sin − = x x 所以 sin cos xdx x c = − + 例2. 求经过(1,3)点,且其任意一点( , ) x y 处的 切线的斜率为 2 3x 的曲线方程。 解 设曲线方程y F x = ( ),则 2 F x x ( ) 3 = 因为 3 2 ( )' 3 x x = 所以 2 3 F x x dx x c ( ) 3 = = + 得曲线族 3 y x c = + 将x y = = 1, 3代入得c = 2。故所求曲线为 3 y x = + 2

二、不定积分的性质和基本积分公式 性质1(f(x)ax)'=f(x) 或 d f(x)dx=f(x)dx 证 设F'(x)=f(x),则 f(x)dx=F(x)+c 故 (f(x))'=(F(x)+c)'=F'(x)=f(x) 而 d f(x)dx=(f(x)dx)'dx=f(x)dx 性质2」∫'(x)c=f(x)+c或d(x)=f(x)+c 证因(f(x)'='(x)故f(x)为f'(x)的原函数。则 ∫f'(x)=f(x)+c,从而∫df(x)=∫f(x)dk=f(x)+c 10
10 二、不定积分的性质和基本积分公式 性质 1 ( ( ) )' ( ) f x dx f x = 或 d f x dx f x dx ( ) ( ) = 证 设F x f x '( ) ( ) = ,则 f x dx F x c ( ) ( ) = + 故 ( ( ) )' ( ( ) )' '( ) ( ) f x dx F x c F x f x = + = = 而 d f x dx f x dx dx f x dx ( ) ( ( ) )' ( ) = = 性质 2 f x dx f x c '( ) ( ) = + 或 df x f x c ( ) ( ) = + 证 因 ( ( ))' '( ) f x f x = 故 f x( ) 为 f x'( ) 的 原 函 数 。 则 f x dx f x c '( ) ( ) = + ,从而 df x f x dx f x c ( ) '( ) ( ) = = +

性质3∫f(x)d=k∫f(x)d(飞≠O) 证 因为时(a)y=对(x), (k[f(x)dx)'=kf(x) 故 (kf(x)dx)=(k f(x)dx) 所以 「f(x)d=kf(x)d 性质4f)±gxdk=∫f)d可gx)d 证因为(fx)±8(xy=f(,±8) (∫f(x)dk±∫g(x)dy=fx)±g(x) 故 (fa)±gxdy=(fx)d±gx)) 11
11 性质 3 kf x dx k f x dx ( ) ( ) = ( 0) k 证 因为 ( ( ) ) ( ) kf x dx kf x = , ( ( ) ) ( ) k f x dx kf x = 故 ( ( ) ) ( ( ) ) kf x dx k f x dx = 所以 kf x dx k f x dx ( ) ( ) = 性质 4 [ ( ) ( )] ( ) ( ) f x g x dx f x dx g x dx = 证 因为 ( [ ( ) ( )] ) ( ) ( ) f x g x dx f x g x = ( ( ) ( ) ) ( ) ( ) f x dx g x dx f x g x = 故 ( [ ( ) ( )] ) ( ( ) ( ) ) f x g x dx f x dx g x dx =

公式: (I)∫0d=c (2) xd= *1 +C a+1 (3) ∫片dk=in+c (4) a'dx= a -+C lna (5) le"dx=e*+c (6) sinxdx =-cosx+c (7) cosxdx sinx+c (8) sec2xdk=tanx+c (9) csc2xdx =-cotx+c (0) 1-x2 -dx arcsinx+c=-arccosx+c =aretanx+c=-arccotx+o (D 12
12 公式: ⑴ 0dx c = ⑵ 1 1 x x dx c + = + + ⑶ 1 dx x c ln x = + ⑷ ln x x a a dx c a = + ⑸ x x e dx e c = + ⑹ sin cos xdx x c = − + ⑺ cos sin xdx x c = + ⑻ 2 sec tan xdx x c = + ⑼ 2 csc cot xdx x c = − + ⑽ 2 1 arcsin arccos 1 dx x c x c x = + = − + − ⑾ 2 1 arctan cot 1 dx x c arc x c x = + = − + +