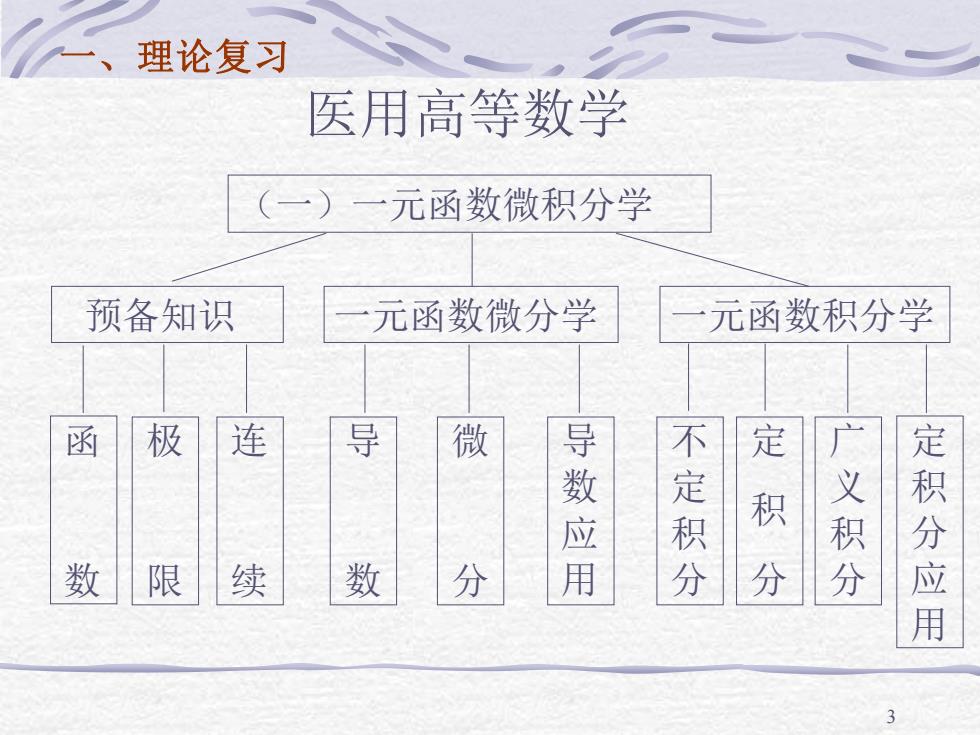
理论复习 医用高等数学 (一)一元函数微积分学 预备知识 元函数微分学 元函数积分学 函 极 连 导 微 定 不定积分 广 数 限 续 数 分 数应用 积分 义积分 定积分应用
3 医用高等数学 (一)一元函数微积分学 预备知识 一元函数微分学 一元函数积分学 函 数 极 限 连 续 导 数 微 分 导 数 应 用 定 积 分 不 定 积 分 广 义 积 分 定 积 分 应 用 一、理论复习
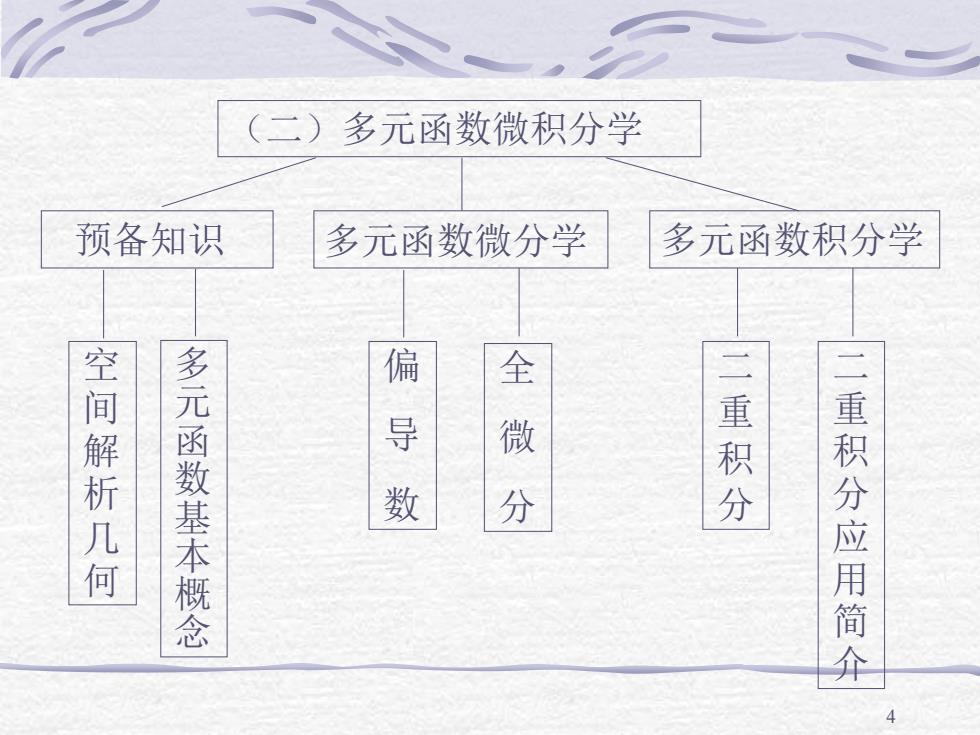
(二)多元函数微积分学 预备知识 多元函数微分学 多元函数积分学 偏 空间解析几何 多元函数基本概念 导数 分 二重积分 二重积分应用简介
4 (二)多元函数微积分学 预备知识 多元函数微分学 多元函数积分学 空 间 解 析 几 何 多 元 函 数 基 本 概 念 偏 导 数 全 微 分 二 重 积 分 应 用 简 介 二 重 积 分
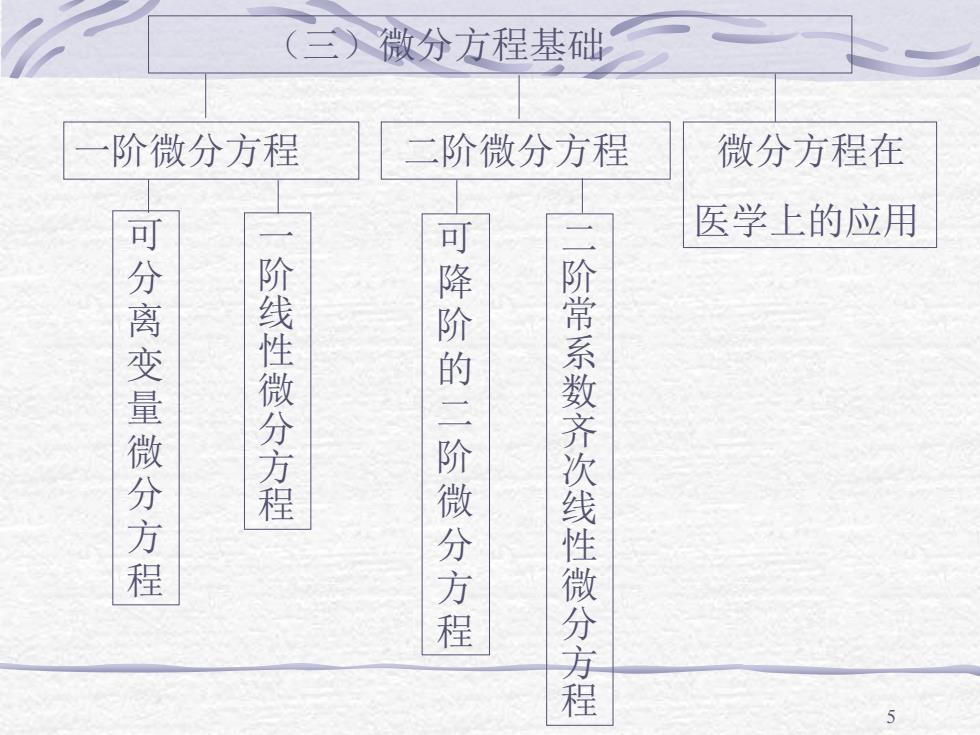
(三)微分方程基础 阶微分方程 二阶微分方程 微分方程在 医学上的应用 可分离变量微分方程 阶线性微分方程 可降阶的二阶微分方程 阶常系数齐次线性微分方程
5 (三)微分方程基础 一阶微分方程 可 分 离 变 量 微 分 方 程 一 阶 线 性 微 分 方 程 二 阶 常 系 数 齐 次 线 性 微 分 方 程 可 降 阶 的 二 阶 微 分 方 程 二阶微分方程 微分方程在 医学上的应用

二、例题分析 期末考试模拟试卷(一) (一)选择题(每小题给出选择只有一项符合题目要求) 1.设函数f(x)的定义域为(0,1], p(x)=1-lnx,则复合函数f[p(x)]的定义域为()。 A.(0,1)B.(0,+∞)C.(1,e]D.[1,e) 解因为f(x)的定义域为(0,] 故0<p(x)=1-lnx≤1 所以lnx≥0,且lnx<1 即x≥1且x<e 因此f(x]的定义域为H,e),选D
6 二、例题分析 期末考试模拟试卷(一) (一)选择题(每小题给出选择只有一项符合题目要求) 1.设函数 f x( )的定义域为(0,1], ( ) 1 ln x x = − ,则复合函数 f x [ ( )] 的定义域为( )。 A.(0,1) B.(0,+∞) C.(1,e] D.[1,e) 解 因为 f x( )的定义域为(0,1] 故 0 ( ) 1 ln 1 = − x x 所以 ln 0 x ,且ln 1 x 即 x 1且x e 因此 f x [ ( )] 的定义域为[1,e),选 D

2.设f(x)=ex,则 nh等于() A-1+c B.+c X X C.-Inx+c D.Inx+c 解「f'(Inx)dlnx=flnx)+c 因f(x)=e,f0nx)=enx=1 放/0n"=+c,选B
7 2.设 ( ) x f x e− = ,则 f x (ln )dx x 等于( ) A. 1 c x − + B. 1 c x + C.− + ln x c D.ln x c + 解 f x d x f x c (ln ) ln (ln ) = + 因 ( ) x f x e− = , ln 1 (ln ) x f x e x − = = 故 f x (ln ) 1 dx c x x = + ,选 B

3.下列广义积分收敛的是(一。) A C.dD.∫k 广f22wm 解 厂w2r 故选B 说明:可子xr=r= 广,在p时收领,在p<级敌
8 3.下列广义积分收敛的是( ) A. 1 1 dx x + B. 1 1 dx x x + C. 1 xdx + D. 1 3 2 1 dx x + 解 1 1 1 dx x 2 | x + + = = + 1 2 1 1 1 dx x2 | 2 x x + − + = − = 故 选 B 说明:实际 1 xdx + 3 2 1 2 | 3 x + = = 1 3 2 1 dx x + 1 3 1 3 | x + = = 1 1 p dx x + ,在 p 1时收敛,在 p 1时发散

4. 微分方程y”+2y+y=0的通解为( A.y=c+ce x B.y=ce C.y=e *(c+cx) D.y=ce *+c,e* 解特征方程 λ2+2元+1=0 即(九+1)2=0 特征根 2=元=-1 故通解 y=ce +cxe*=(c+cx)e x 所以 选C 9
9 4.微分方程y y y + + = 2 0的通解为( ) A. 1 2 x y c c e − = + B. 1 x y c e − = C. 1 2 ( ) x y e c c x − = + D. 1 2 x x y c e c e − = + 解 特征方程 2 + + = 2 1 0 即 2 ( 1) 0 + = 特征根 1 2 = = −1 故通解 1 2 x x y c e c xe − − = + 1 2 ( ) x c c x e − = + 所以 选 C

5.设函数f在x点可导,则1m-)-/ h>0 h A.与x,h都有关 B.仅与h有关,而与x无关 C.与x,h都无关 D.仅与x有关,而与h无关 解mf-)-f)-mf--f)=-fx) h-→0 h h-→0 -h 此极限只与x有关,而与h无关 故选D。 10
10 5.设函数 f x( )在 0 x 点可导,则 0 0 0 ( ) ( ) lim h f x h f x → h − − ( ) A.与 0 x h, 都有关 B.仅与h有关,而与 0 x 无关 C.与 0 x h, 都无关 D.仅与 0 x 有关,而与h无关 解 0 0 0 ( ) ( ) lim h f x h f x → h − − 0 0 0 0 ( ) ( ) lim ( ) h f x h f x f x → h − − = − = − − 此极限只与 0 x 有关,而与h无关 故选 D

、填空题(把答案填在题目中的横线上) 6.函数fx)=V4-+1 在连续区间为 √x-1 解f(x)为初等函数,故定义区间为连续区间 4-x2≥0,且x2-1>0 即-2≤x≤2,且1<x和x<-1 即 -2≤x<-1和1<x≤2 故定义域[-2,-1)U(1,2],也为定义区间 所以连续区间为[-2,-1)U(1,2] 11
11 二、填空题(把答案填在题目中的横线上) 6.函数 2 2 1 ( ) 4 1 f x x x = − + − 在连续区间为_______ 解 f x( )为初等函数,故定义区间为连续区间 2 4 0 − x ,且 2 x − 1 0 即 − 2 2 x ,且1 x和x −1 即 − − 2 1 x 和1 2 x 故定义域[ 2, 1) (1,2] − − ,也为定义区间 所以连续区间为 [ 2, 1) (1,2] − −

解 2 1+x+x2-3 =-lim- (x-1)(x+2) x1(x-1)(1+x+x2) x+2 =-lim x11+x+x2 =-1 所以, 填-1 12
12 7. 3 1 1 3 lim( ) x→ 1 1 x x − = − − ________ 解 2 3 2 1 1 1 3 1 3 lim( ) lim 1 1 (1 )(1 ) x x x x → → x x x x x + + − − = − − − + + 2 1 ( 1)( 2) lim ( 1)(1 ) x x x → x x x − + = − − + + 2 1 2 lim 1 1 x x → x x + = − + + = − 所以, 填 −1