
上讲提要 1.换元积分法; 2.分部积分法: 3.有理函数积分。 3
3 上 讲 提 要 1. 换元积分法; 2. 分部积分法; 3.有理函数积分
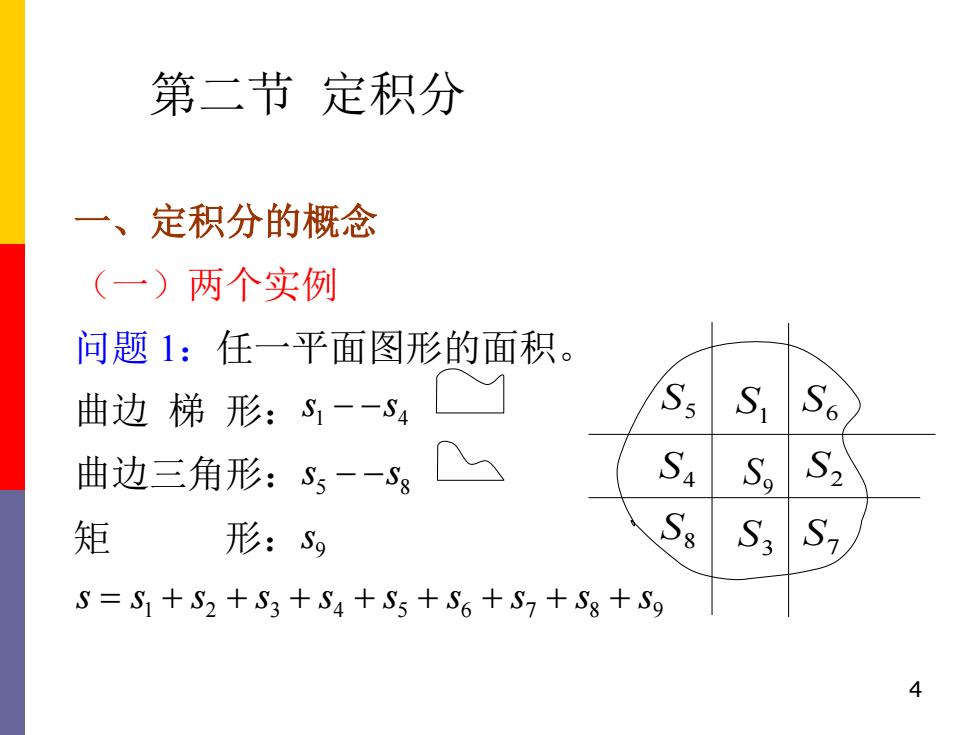
第二节定积分 一、定积分的概念 (一)两个实例 问题1:任一平面图形的面积。 曲边梯形:S,--S4 Ss S S6 曲边三角形:S--Sg So S2 矩 形:Sg Se S3 S=S1+S2+S3+S4+S5+S6+S7+S8+Sg 4
4 第二节 定积分 一、定积分的概念 (一)两个实例 问题 1:任一平面图形的面积。 曲边 梯 形: 1 4 s s − − 曲边三角形: 5 8 s s − − 9 S 矩 形: 9 s 1 2 3 4 5 6 7 8 9 s s s s s s s s s s = + + + + + + + + S2 S1 S3 S4 S5 S6 S7 S8
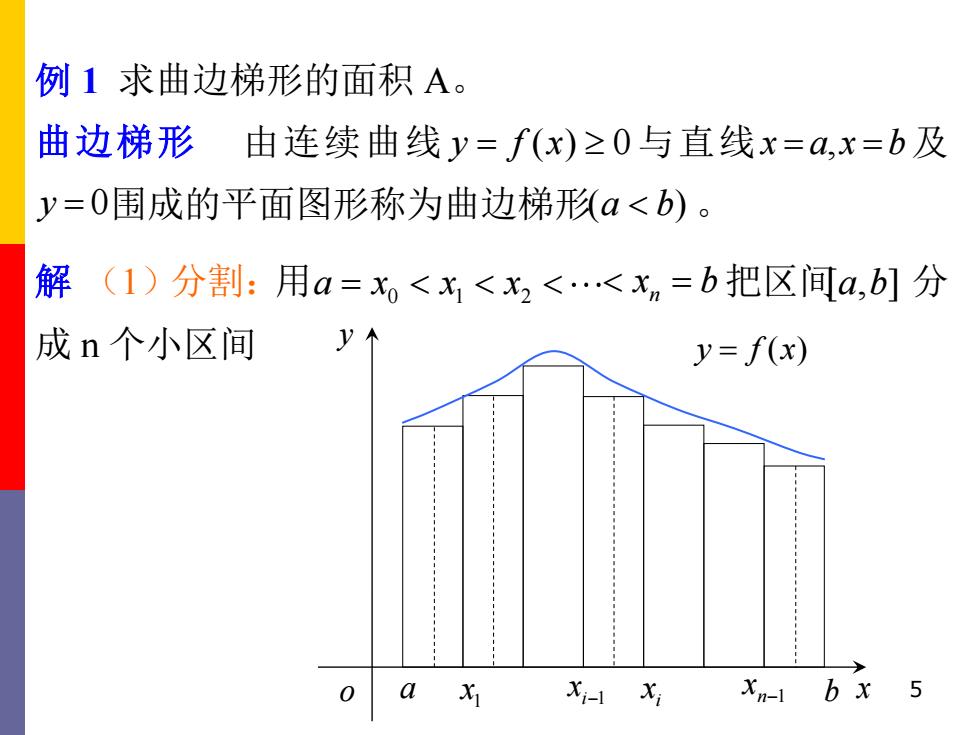
例1求曲边梯形的面积A。 曲边梯形 由连续曲线y=f(x)≥0与直线x=a,x=b及 y=0围成的平面图形称为曲边梯形队a<b)。 解(1)分割:用a=x。<x<x2<<xn=b把区间a,b]分 成n个小区间 y=f(x) a X-1 Xn-1 b x 5
5 例 1 求曲边梯形的面积 A。 曲边梯形 由连续曲线 y f x = ( ) 0与直线x a x b = = , 及 y = 0围成的平面图形称为曲边梯形( ) a b 。 解 (1)分割:用 0 1 2 a x x x = n = x b 把区间[ , ] a b 分 成 n 个小区间 y f x = ( ) y o a b x 1 x i 1 x − i x n 1 x −

[xo,],…,[x-1,x],…,[xn-1,xn]。小区间长度 △x,=x,-x1。得n个小曲边梯形面积,记为 △4,i=1,2,…,n (2)近似代替: y=f(x) V5∈[x-,x], △4≈f(5)△xi=1,2,5,n (3)求和: A=2a4f54 X-15X Xn-15nbx
6 0 1 1 1 [ , ], ,[ , ], ,[ , ] i i n n x x x x x x − − 。 小 区 间 长 度 i i i 1 x x x = − − 。 得 n 个小曲边梯形面积,记为 Ai ,i n =1,2, , (2)近似代替: 1 [ , ] i i i x x − , ( ) 1,2, , = A f x i n i i i (3)求和: 1 1 ( ) n n i i i i i A A f x = = = y f x = ( ) y o a b x 1 x i 1 x − i x n 1 x − 1 i n

(4)求和的极限 A=lm∑f(5Ay -0 其中=max{△x,} 1<i<n 问题2.变速直线运动的路程 例2.直线运动的速度v=v(t)≥0,在[T,T,]上连续, 求在时间间隔[T,T,]内物体所经过的路程S。 解(1)分割:用n+1个分点T=t<t<t,2<…<tn=T, 把区间[T,T,]分割成n个小区间 7
7 (4)求和的极限 0 1 lim ( ) n i i i A f x → = = 其中 1 max i i n x = 问题 2.变速直线运动的路程 例 2. 直线运动的速度v v t = ( ) 0,在 1 2 [ , ] T T 上连续, 求在时间间隔 1 2 [ , ] T T 内物体所经过的路程 S。 解(1)分割:用n +1个分点T t t t t T 1 0 1 2 2 = =n , 把区间 1 2 [ , ] T T 分割成n个小区间

[T,T],…,[T,T],[T,Tn] 小区间长度△t,=t,-41i=1,2,…,n,得n个小段路程, 记为 △S,i=1,2,…,n (2)近似替代 Vt,∈[t-1,t,] AS,≈v(t)△ti=1,2,…,n (3)求和 S=AS,=Ev(r.)AL i-1 i-1 (4)求和的极限 S=lim∑(z,)At 2-→0 i=l 其中=max{At} l≤i≤n 8
8 0 1 1 1 [ , ], ,[ , ], [ , ] T T T T T T i i n n − − 小区间长度 1 1,2, , i i i t t t i n = − = − ,得 n 个小段路程, 记为 Si,i n =1,2, , (2)近似替代 1 [ , ] i i i t t − ( ) 1,2, , i i i = S v t i n (3)求和 1 1 ( ) n n i i i i i S S v t = = = (4)求和的极限 0 1 lim ( ) n i i i S v t → = = 其中 1 max i i n t =

(二)概念 定义3-3设函数f(x)在区间[a,b]上有定义,任取分点 a=Xo<x1<X2<…<Xn=b 将[a,b]分成n个小区间,在每个小区间[x1,x]上任取 一点(x1≤,≤x),作和式∑f(5)△x,(其中 i=l △x,=x,-x,1),如果不论对[a,b]如何分法,以及5如何取 法,只要当元=max{}→0时,和式∑f(怎Ax的极 限存在,则称此极限为f(x)在[a,b]上的定积分,记为 fx)d。 9
9 (二)概念 定义 3-3 设函数 f x( )在区间[a,b]上有定义,任取分点 a x x x x b = = 0 1 2 n 将[a,b]分成 n 个小区间,在每个小区间 1 [ , ] i i x x − 上任取 一 点 1 ( ) i i i i x x − ,作和式 1 ( ) n i i i f x = (其中 i i i 1 x x x = − − ),如果不论对[a,b]如何分法,以及i如何取 法,只要当 1 max 0 i i n x = → 时,和式 1 ( ) n i i i f x = 的极 限存在,则称此极限为 f x( )在[a,b]上的定积分,记为 ( ) b a f x dx

即心=m∑f八A,其中称fx)为被积函数, i=l f(x)dc为被积表达式,x为积分变量,a和b分别为积分 下限和积分上限,[a,b]为积分区间,∑f(5△x为积分和。 实例1,A=f(x)d;实例2,S=∫)d: 补充定义心fd=-心f(x),f(xk=0 结论1f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。 结论2f(x)在区间[a,b]上有界,且只有有限个间断点, 则f(x)在[a,b]上可积。 10
10 即 0 1 ( ) lim ( ) n b i i a i f x dx f x → = = ,其中称 f x( )为被积函数, f x dx ( ) 为被积表达式,x为积分变量,a 和 b 分别为积分 下限和积分上限,[a,b]为积分区间, 1 ( ) n i i i f x = 为积分和。 实例 1, ( ) b a A f x dx = ;实例 2, ( ) b a S v t dt = ; 补充定义 ( ) ( ) b a a b f x dx f x dx = − , ( ) 0 a a f x dx = 结论 1 f x( )在区间[a,b]上连续,则 f x( )在[a,b]上可积。 结论 2 f x( )在区间[a,b]上有界,且只有有限个间断点, 则 f x( )在[a,b]上可积
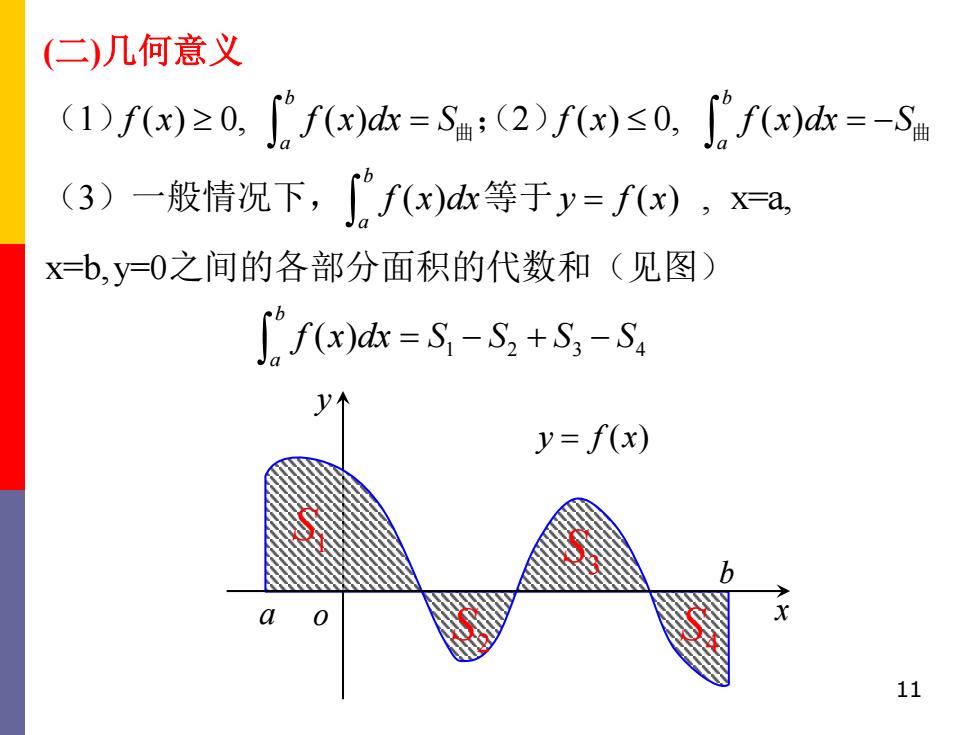
(二)几何意义 (1)f(x)≥0,Cfx)dr=S猫:(2)fx)≤0,Cfx)d=-S (3)一般情况下,fx)dk等于y=f(x),x=a x=b,y=O之间的各部分面积的代数和(见图) [f(x)dx=S,-S:+S,-Sa y=f(x) 11
11 (二)几何意义 (1)f x( ) 0, ( ) b a f x dx S = 曲;(2) ( ) 0, ( ) b a f x f x dx S = − 曲 (3)一般情况下, ( ) b a f x dx 等于y f x = ( ) , x=a, x=b,y=0之间的各部分面积的代数和(见图) 1 2 3 4 ( ) b a f x dx S S S S = − + − y a o x b y f x = ( ) S1 S2 3 S 4 S

例1用定义计算xd 解f(x)=x2在[0,1]上连续,故f(x)在[0,1]上可积, 将[0,1]分成n等分,分点 x= (i=0,1,2,…n) n 每个小区间长度 x=1取511,2,m n n 故r-m2号m2r i=1 nn n-→on =lim n(n+1)(2n+1)_1 6n 3 12
12 例 1 用定义计算 1 2 0 x dx 解 2 f x x ( ) = 在[0,1]上连续,故f x( ) 在[0,1]上可积, 将[0,1]分成 n 等分,分点 (i=0,1,2, ) i i x n n = 每个小区间长度 1 , = (i=1,2, ) i i i x n n n = 取 故 1 2 2 2 3 0 1 1 1 1 lim ( ) lim n n n n i i i x dx i → → = = n n n = = ( )( ) 3 1 2 1 1 limn 6 3 n n n → n + + = =