
第三章 多维随机变量及其分布 第一节二维随机变量 一、二维随机变量及其分布函数 定义设随机试验的基本空间为2,和是定义在2上的两个随 机变量,由它们构成的向量(X,)叫做二维随机变量. 二维随机变量(X,)可以看作是xOy面上的随机点,它们的取值是 xoy面上的一个定点(x,y)·X,Y)可能落在xoy面上的有限个点处, 也可能落在xOy面上某个区域内的所有点上.我们把二维随机变量分成 离散型和连续型两类
定义 设随机试验E的基本空间为Ω,X和Y是定义在Ω上的两个随 机变量,由它们构成的向量(X,Y)叫做二维随机变量. 第三章 多维随机变量及其分布 第一节 二维随机变量 一、二维随机变量及其分布函数 二维随机变量 (X,Y) 可以看作是 xoy 面上的随机点,它们的取值是 xoy 面上的一个定点(x,y).(X,Y) 可能落在 xoy 面上的有限个点处, 也可能落在 xoy 面上某个区域内的所有点上.我们把二维随机变量分成 离散型和连续型两类.

x,y) 定义设(X,)为二维随机变量,对任意实数x,y,二元函数 F(x,y)=P{X≤x,Y≤y以 称为二维随机变量X,)的分布函数,或称为X与Y的联合分布函 数. 注:1°规定{X≤x,Y≤y}表示事件{X≤x}与Y≤y}的积事 件. 2°分布函数Fx,y)在点(x,y)处的值,就是(X,Y)的取 值落在矩形一0<X≤x,一o<Y≤y上的概率
y x o (x, y) 定义 设 (X,Y) 为二维随机变量,对任意实数x,y,二元函数 称为二维随机变量 (X,Y) 的分布函数,或称为X与Y的联合分布函 数.. F(x, y) = P{X x,Y y} 注:1°规定{ X ≤x , Y ≤ y }表示事件 { X ≤x }与{Y ≤ y }的积事 件. 2°分布函数 F(x,y) 在点(x,y) 处的值,就是(X,Y)的取 值落在矩形 -∞< X ≤ x , -∞<Y ≤ y 上的概率.

二维随机变量(X,)的分布函数F(x,y)具有性质: 1°O≤Fx,y),且对任意x,y有 F(-0,y)=0,F(x,-0∞)=0, F(-00,-00)=0,F(+00,+o0)=1 2°F(x,y)是变量x和y的单调不减函数. 3°x,y)关于x右连续,关于y也右连续 4°(X,Y)落在矩形区域x1<Xx2,y,<Y≤y2上的概率为 P{x1<X≤x2,y1<Y≤y2}=F(x2,y2)-F(x1,y2)-F(x2,y1)+F(x1,y1) y2 X2
二维随机变量(X,Y)的分布函数F(x,y)具有性质: 1°0≤F(x,y),且对任意x,y有 . 2°F(x,y)是变量x和y的单调不减函数. 3°F(x,y)关于x右连续,关于y也右连续 4°(X,Y)落在矩形区域x1<X≤x2,y1<Y≤y2上的概率为 . F(−, y) = 0, F(x,−) = 0, F(−,−) = 0, F(+,+) =1 { , } ( , ) ( , ) ( , ) ( , ) 1 2 1 2 2 2 1 2 2 1 1 1 P x X x y Y y = F x y − F x y − F x y + F x y y x o 2 y 1 y 1 x 2 x

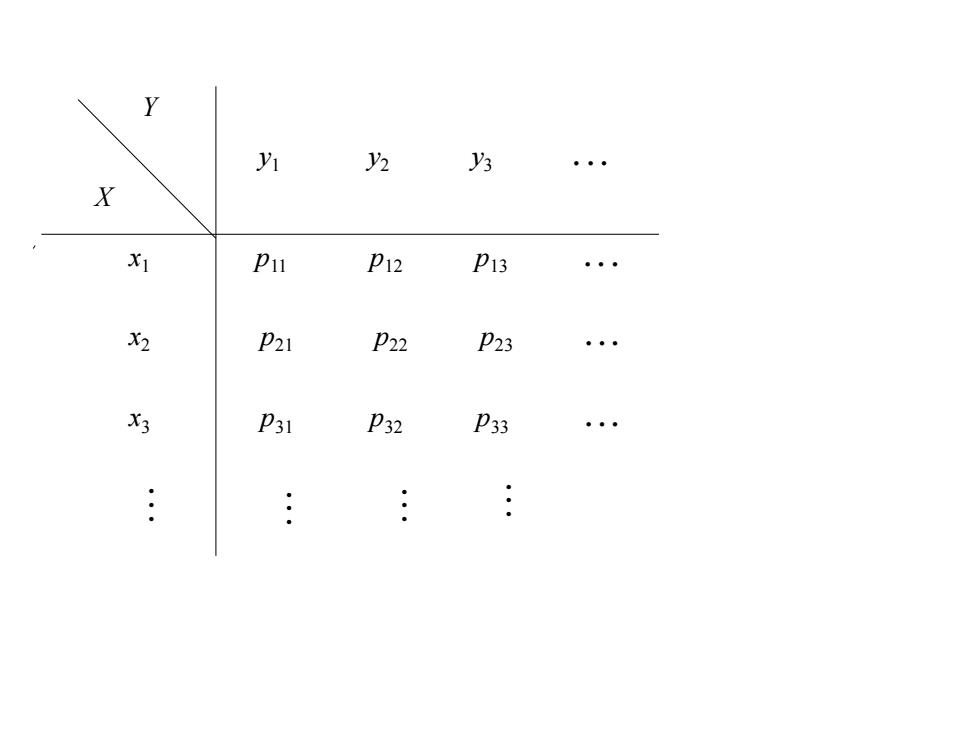
二、二维离散型随机变量 定义若二维随机变量(X,)所有可能取的值是有限 对或可列无穷多对,则称(X,)为二维离散型随机变 量。设二维离散型随机变量(X,)所有可能取值为 (x,yji=1,2,…,j=1,2,… 记 P=P{X=x,Y=y}i,j=1,2,… (*) 且有 P≥0,∑P,=1 则称(*)式为(X,)的概率分布或X与Y的联合分布律
定义 若二维随机变量(X,Y) 所有可能取的值是有限 对或可列无穷多对,则称(X,Y) 为二维离散型随机变 量. 设二维离散型随机变量(X,Y) 所有可能取值为 记 (*) 且有 则称(*)式为(X,Y)的概率分布或X与Y的联合分布律. (xi , y j ), i =1,2, , j =1,2, pi j = P{X = xi ,Y = y j } i, j =1,2, = i j ij ij p p , 0, 1 二、二维离散型随机变量
y 2 3 X1 P11 P12 P13 X2 P21 P22 P23 X3 P31 p32 P33 …:
Y y1 y2 y3 . . . X x1 p11 p12 p13 . . . x2 p21 p22 p23 . . . x3 p31 p32 p33 . . . . . . . . . . . . . .

例1设试验E为掷一颗骰子,观察出现的点数,定 义两个随机变量如下 X表示骰子出现的点数 Y=. 1,当出现奇数点时 2,当出现偶数点时 试求X与Y的联合分布律. 解(X,)可能取值为(1,1)、(1,2)、(2,1)、(2,2)、(3,1)人(3,2)、 (4,1)、(4,2)、(5,1)、(5,2)、(6,1)、(6,2). P=P(X-LY-B-P(X-BP(Y-IIX-1-1x1-1 66 p12=P{X=1,Y=2}=P{X=1}P{Y=2|X=1}=二×0, 6
例1 设试验E为掷一颗骰子,观察出现的点数,定 义两个随机变量如下 X 表示骰子出现的点数. 试求X与Y的联合分布律. = 2, . 1, , 当出现偶数点时 当出现奇数点时 Y 解 (X,Y)可能取值为(1,1)、(1,2)、(2,1)、(2,2)、(3,1)、(3,2)、 (4,1)、(4,2)、(5,1)、(5,2)、(6,1)、(6,2). , 6 1 1 6 1 { 1, 1} { 1} { 1| 1} p11 = P X = Y = = P X = P Y = X = = = 0, 6 1 { 1, 2} { 1} { 2 | 1} p12 = P X = Y = = P X = P Y = X = =

同理 1 p2=p31=P42=P51=P62=6 P21=P32=P41=P52=P61=0 1 2 1/6 0 2 0 1/6 3 1/6 0 W 0 1/6 5 1/6 0 6 0 1/6 二维离散型随机变量(X,)的分布函数为F(x,y)=∑P, x≤x y≤y
同理 , 6 1 p22 = p31 = p42 = p51 = p62 = 0 p21 = p32 = p41 = p52 = p61 = Y X 1 2 1 1 / 6 0 2 0 1 / 6 3 1 / 6 0 4 0 1 / 6 5 1 / 6 0 6 0 1 / 6 二维离散型随机变量(X,Y)的分布函数为 . = y y x x ij j i F(x, y) p

三、二维连续型随机变量 定义设二维随机变量(X,)的分布函数为Fx,y), 如果存在非负函数fx,y),使对任意xy有 F(x,)=∫∫fx,dd (=∫∫'f,vdid 则称(X,)为二维连续型随机变量,称x,y)为X,)的概率密度或X、Y的 联合概率密度 性质1 f(x,y)≥0. 性质2 ∫fxy=1
三、二维连续型随机变量 定义 设二维随机变量(X,Y)的分布函数为F(x,y), 如果存在非负函数f(x,y),使对任意x,y有 . 则称(X,Y)为二维连续型随机变量,称f(x,y)为(X,Y)的概率密度或X、Y的 联合概率密度. − − = x y F(x, y) f (x, y)dxdy = − − x y f (u, v)dudv f (x, y) 0 + − + − f (x, y)dxdy =1 性质1 . 性质2

性质3在x的连续点处有fK,)=0Fx》 Oxoy 性质4设G为xOy面上一个区域,点(X,)落在G内的概 率为 P((X.Y)EG)=[[f(x.y)dxdy. 例2设二维随机变量(X,)的概率密度为 x≥0,y≥0, 0, 其它 (1)求k:(2)求分布函数Fxy):(3)求P{X> 解(1)由∫∫fx,ydy=1.而 ∫∫fax,y)ddy=∫。∫ke2+drdy
性质3 在f(x,y)的连续点处有 . 性质4 设G为xoy面上一个区域,点(X,Y)落在G内的概 率为 . x y F x y f x y = ( , ) ( , ) 2 = G P{(X,Y) G} f (x, y)dxdy 例2 设二维随机变量(X,Y)的概率密度为 (1)求k;(2)求分布函数F(x,y);(3)求P{X> Y}. = − + 0, . , 0, 0, ( , ) (2 3 ) 其它 k e x y f x y x y 解 (1)由 .而 + − + − f (x, y)dxdy =1 + + − + + − + − = 0 0 (2 3 ) f (x, y)dxdy k e dxdy x y

则有k=6. (2)当x>0,y>0时 F(x,y)=∫∫'fx,y)dxdy=∫J6e2x+drd =(1-e2x)1-e-3y). 对于其它点x,y),由于fxy)=0,则F(x,y)=0. 于是 小0--n2 0,其它
6 d d 0 3 0 2 k k e x e y x y = = + − + − 则有k =6. (2)当 x>0,y>0时 . 对于其它点(x,y),由于f (x,y)=0,则F(x,y)=0. 于是 − + − − = = x y x y x y F x y f x y x y e x y 0 0 (2 3 ) ( , ) ( , )d d 6 d d (1 )(1 ) 2x 3y e e − − = − − − − = − 0, . (1 )(1 ), 0, 0, ( , ) 2 3 其它 e e x y F x y x y y x o G1