
第一章随机事件与概率 自然界中各种现象可以区分为两种:确定性现象与随机现象, 确定性现象:在一定条件下必然会出现的现象 随机现象:在一定的条件下,可能出现多种结果,而在试验之前无法预知其 确切的结果,也无法控制, 概率论与数理统计是研究和揭示随机现象统计规律性的一门数学学科, 第一节随机事件及其运算 随机试验与随机事件 随机试验:具有以下特点的试验称为随机试验: 1°试验可以在相同条件下重复进行: 2°试验可能出现的结果不只一个,在试验之前知道所有可能的结果: 3°试验结束后会出现哪一个结果是随机的(无法事先知道,也无法控制 通常用字母E表示随机试验(以后简称试验) 例如:
第一章 随机事件与概率 自然界中各种现象可以区分为两种:确定性现象与随机现象. 确定性现象:在一定条件下必然会出现的现象. 随机现象:在一定的条件下,可能出现多种结果,而在试验之前无法预知其 确切的结果,也无法控制. 概率论与数理统计是研究和揭示随机现象统计规律性的一门数学学科. 第一节 随机事件及其运算 一、随机试验与随机事件 随机试验:具有以下特点的试验称为随机试验: 1°试验可以在相同条件下重复进行; 2°试验可能出现的结果不只一个,在试验之前知道所有可能的结果; 3°试验结束后会出现哪一个结果是随机的(无法事先知道,也无法控制). 通常用字母E表示随机试验(以后简称试验). 例如:

例如: E,:抛一枚硬币,观察正、反面出现的情况, E,:掷一颗骰子,观察出现的点数 E:向一个靶子发射一颗子弹,观察打中的环数: E:检查一大批灯泡的寿命. 基本事件(样本点,或0):一次试验可能出现的每一个直接的结果。也就 是随机试验不能够再分解的结果, 如E,有两个基本事件={出现正面},e2{出现反面} E2有六个基本事件:e,={出现i点},i=12,…,6 基本空间(样本空间2或S或U):全体基本事件的集合
例如: :抛一枚硬币,观察正、反面出现的情况. :掷一颗骰子,观察出现的点数. :向一个靶子发射一颗子弹,观察打中的环数. :检查一大批灯泡的寿命. E1 E2 E3 E4 基本事件(样本点,或 ): 一次试验可能出现的每一个直接的结果.也就 是随机试验不能够再分解的结果. 如 有两个基本事件:={出现正面},={出现反面}. 有六个基本事件: ={出现 点}, . e E1 1 e E2 i e i i =1,2, ,6 2 e 基本空间(样本空间, 或 S 或 U ): 全体基本事件的集合.

如E的基本空间为2={e1,e2}:E,的基本空间为 2={ee2,e3,e4e5e6}或2={1,2,3,4,5,6}. 随机事件:试验的每一个可能结果.用大写字母A,B,C等表示, 随机事件也就是基本空间的子集,即若干基本事件做成的集合. 如在E2中,“出现偶数点”的事件可表示=2,4,6}, “出现奇数点”的事件可表示为B={1,3, 而C={1,2,3表示事件“出现的点数不超过3. 事件发生:当事件A所包含的基本事件有一个出现,就说事件4发生了,香 则就说事件4未发生 必然事件:一定发生的事件,也就是基抱空 不可能事件:一定不发生的事件.记 二、事件的关系与运算 试验E的基本空间为2,A、B、A(k=1,2,)为E中的事件 1.包含:如果事件A发生必然导致事件8发生.则称事件B包含事件A, 记作ACB或B⊙A
不可能事件:一 定 不 发 生 的 事 件 . 记 为 . 如 的基本空间为 ; 的基本空间为 = {e1 ,e2 ,e3 ,e4 ,e5 ,e6 } 或 {1,2,3,4,5,6}. { , } 1 2 = e e E1 E2 = 随机事件:试验的每一个可能结果.用大写字母 A,B,C 等表示. 随机事件也就是基本空间的子集,即若干基本事件做成的集合. 如在 中,“出现偶数点”的事件可表示为 {2,4,6}, “出现奇数点”的事件可表示为 ={1,3, 5}, B 而 C = {1,2,3}表示事件“出现的点数不超过3”. E2 A = 一定发生的事件 , 也就是基本空 间 . 必然事件: 事件发生:当事件 所包含的基本事件有一个出现,就说事件 发生了,否 则就说事件 未发生. A A A 试验 的基本空间为 , 、 、 ( =1,2,…)为 中的事件. 1.包含:如果事件 发生必然导致事件 发生.则称事件 包含事件 , 记作 或 . E A B Ak k E A B B A A B B A 二、事件的关系与运算

ACB就是在A中的基本事件,一定都含在B中.对任一事件A都 有中cAC2. 2.相等:如果有ACB,BA同时成立,则称事H与事件B相等,记作 A=B·A=B就是事件A与事件B所包含的基本事件完全相同. 3。事件的和:“事制与事件B至少有一个发生”,这样的一个事件称 为 A B AUB 事件白喜就科科1件B所包含的基本事件放在一起作成的事 件。 在E,中,A={2,4,6},C={1,2,3}.AUC={1,2,3,4,6} 对于任一事件A,有 AUA=AAU中=A AU2=2 4.事件的积:“事件4与事件同时发生”,这样的事件称为事件4与事件 B的积或交,记为A∩B或AB AB就是把事件A与事件B所公有的基本事件放在一起作成的事件. 在B2中,AC{2},BC={1,3},AB=中 对于任一事件A,有 AA三A AQ=A A中=小
就是在 中的基本事件,一定都含在 中.对任一事件 都 有 . A B B A A A 2.相等:如果有 , 同时成立,则称事件 与事件 相等,记作 A = B .A = B 就是事件 与事件 所包含的基本事件完全相同. A B B A B A B A AB 就是把事件 A 与事件 B 所公有的基本事件放在一起作成的事件. 4.事件的积: “事件 与事件 同时发生” ,这样的事件称为事件 与事件 的积或交,记为 或 . A B A B AB A B 在 E2 中, AC ={2}, BC ={1,3}, AB = . 对于任一事件A,有 AA = A A = A A = 3.事件的和: “事件 与事件 至少有一个发生”,这样的一个事件称 为 事件 与事件 的和或并,记为 . A B A B B 就是把事件 与事件 所包含的基本事件放在一起作成的事 件. A B A B 在 中, ={2,4,6}, ={1,2,3}. ={1,2,3,4,6}. 对于任一事件 ,有 E2 A A C AC A A = A A = A A = A

事件的和与事件的积可以推广到多个事件的情形: 事件A,A2,…,A,的和事件记作AU4,U.UAn或U4 表示事件纠,42,…,A,中至少有一个事件发生”日 事件A,42,,4n的积事件记作A∩4∩∩An或∩4, 表示事件生,A2…,A,同时发生” 可数无穷多个事件4,4,,4,…的和与积分别记作U4与∩4,U4表 示“事件,4,,4,…中至少有一个发生”4,表示“事件4,4,… 同 时发生” 5.事件的差:事件A发生而事件B环发生”,这样的事件称为事4与事 件B的差,记为A-B. 如在E2中,A-C={4,6 对于任一事件A,有 A-A=中,A-中=A,A-2=0 A一B就是A的基本事件中去掉含在B中的,余下的基本事件作成的事 件,6.互不相容(互斥):若事件与事件B不能同时发生(即AB=中),则称事 件A与事件B互不相容或互斥. A与B互不相容,就是A与B不含有公共基本事件
事件的和与事件的积可以推广到多个事件的情形: 事件 的和事件记作 或 , 表示事件“ 中至少有一个事件发生”. A A An , , , 1 2 A1 A2 An A A An , , , 1 2 n i Ai =1 事件 的积事件记作 或 , 表示事件“ 同时发生”. n i Ai =1 A A An , , , 1 2 A1 A2 An A A An , , , 1 2 可数无穷多个事件 的和与积分别记作 与 , 表 示“事件 A1 , A2 , , Ai , i=1 Ai i=1 Ai i=1 Ai 中至少有一个发生”; 表示“事件 同 时 发生”. A1 , A2 , , Ai , i=1 Ai A1 , A2 , , Ai , AB = A 6.互不相容(互斥): 若事件 与事件 不能同时发生(即 ),则称事 件 与事件 B 互不 相容或互斥. A 与 B 互不相容,就是 A 与B 不含有公共基本事件. B A “事件 发生而事件 不发生” ,这样的事件称为事件 与事 件 的差,记为 A− B . 就是 的基本事件中去掉含在 中的,余下的基本事件作成的事 件. A− B A B 如在 E2 中, A − C = {4,6}. 对于任一事件 A ,有 A− A = , A− = A , A− = . 5.事件的差: A B A B

当事件A与B互不相容时,AUB记作A+B: 7.对立(互逆):若A事件与事件B有且仅有一个发生, 即AUB=2且AB=·,则称事件A与事件B为对立事件或互逆事件,其 中事件B叫做事件A的逆事件,记作B=A,事件A叫做事件B的逆事 件,记作A=B 如在E,中,A与B互逆 8.运算规律: 1)AUB=BUA,A∩B=BnA· (2)(AUB)C=ACUBC,(AB)UC=(AUC)(BUC). (3)AUB=AnB,U4=∩4 (4)AnB=AUB,∩4=UA (5)A-B=A-AB=AB
当事件 A 与 B 互不相容时, A B 记作 A+ B . 8.运算规律: (1) A B = B A , A B = B A . (2) (A B)C = AC BC , (AB)C = (AC)(B C) . (3) AB = A B , . = = = 1 k 1 k k Ak A (4) AB = A B , . = = = 1 k 1 k k Ak A (5) A− B = A− AB = AB . 7.对立(互逆):若 事件与事件 有且仅有一个发生, 即 且 ,则 A B 称事件 与事件 为对立事件或互逆事件,其 中事件 叫做事件 的逆事件,记作 ,事件 叫做事件 的逆事 件,记作 . A B = AB = B A B A A B = A B A= B 如在 E2 中, A 与 B 互逆.

例某工人加工三个零件,设4,表示事件 “第i个零件是合格品”式=1,2,3),试用4243表示下列事件: (I)只有第一个零件是合格品: 2)只有一个零件是合格品: (3)至少有一个零件是合格品: (4)最多有一个零件是合格品. 解四个事件分别设为A,B,C,D,则有 (1)A=4424: (2)B=4424U4424,U44249 (3)C=4U4U4(C=AA4月 4)D=A443UB =4424U444U444U4424 或 D=A4 UA4 UA4
“第 个零件是合格品”( =1,2,3),试用 , , 表示下列事 件: 例 某工人加工三个零件,设 Ai 表示事件 i i A1 A2 A3 (1) 只有第一个零件是合格品; (2) 只有一个零件是合格品; (3) 至少有一个零件是合格品; (4) 最多有一个零件是合格品. 解 四个事件分别设为 A , B , C , D ,则有 (1) A = A1 A2 A3 ; (2) B = A1 A2 A3 A1 A2 A3 A1 A2 A3 ; (3) ( ) C = A1 A2 A3 C = A1 A2 A3 ; (4) D = A1 A2 A3 B 或 . = A1 A2 A3 A1 A2 A3 A1 A2 A3 A1 A2 A3 D = A1 A2 A1 A3 A2 A3

第二节概率的古典定义 在一个试验中,有许多随机事件。一个事件在一次试验中可能发生,也 可能不发生.有的事件发生的可能性大,有的事件发生的可能性小。概率就 是用来刻划事件发生的可能性大小的数量指标。 一、概率的统计定义 1.频率 定义1设A为试验E中的一个事件,把试验E在相同条件下重复进行次,如 果事件4发生的次数为”4,则称”4为事件A在n次试验中发生的频率,记为 fn(A),即 h n(4)=”4 设试验B的基本空间为2,A为E中的随机事件,4,42,,4为E中两两 互不相容的事件,则由定义1易知频率具有下述性质: 性质10≤fn(4小≤1. 性质2∫n(2)=1 性质3fn(4U4UU4n)=fn(4)+fn(4)++fn(4m)
在一个试验中,有许多随机事件.一个事件在一次试验中可能发生,也 可能不发生.有的事件发生的可能性大,有的事件发生的可能性小.概率就 是用来刻划事件发生的可能性大小的数量指标. 一、概率的统计定义 设试验 的基本空间为 , 为 中的随机事件, 为 中两两 互不相 E A E A1 , A2 , , Am E 容的事件,则由定义1易知频率具有下述性质: 性质1 0≤ ≤1 f n (A) . 性质2 f n ( ) = 1 . 性质3 f n (A1 A2 Am ) = f n (A1 ) + f n (A2 ) ++ f n (Am ) . 1.频率 定义1 设 A 为试验 E 中的一个事件,把试验 E 在相同条件下重复进行 n 次,如 果事件 发生的次数为 ,则称 为事件 在 次试验中发生的频率,记为 即 A A n n nA A n f (A) n . n n f A A n ( ) = , 第二节 概率的古典定义
上述性质依次称为频率的非负性、规范性、(有限)可 性。堡验证明,当试验进行的次数很大时,事件利的频率 f(4)具有一定的稳定性:即当试验次数n充分大时,频率 (4)总在一个确定的数字附近摆动 例1古代学者摩根(Morgan)、蒲丰(Buffon)和皮尔逊(Peason),分别做 了多次抛掷硬币的试验,观察正面出现的次数,记录结果如表1-1所示 其中n是抛掷硬币的次数,H表示事件“出现正面”,是在次 试验中正面出现的次数)表乐次试验中正面出现的频率. 表1-1 实验者 试验次数 正面出现次数 频率 摩根 2048 1010 0.4932 蒲丰 4040 2048 0.5069 皮尔逊 0.5016 12000 6019 皮尔逊 24000 12012 0.5005
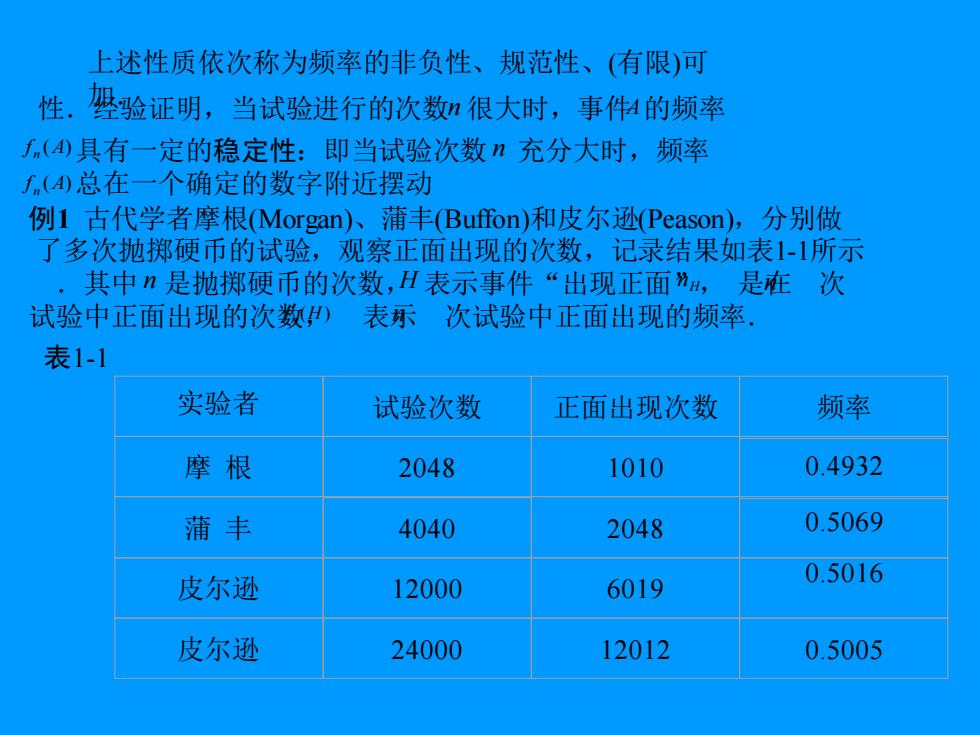
上述性质依次称为频率的非负性、规范性、(有限)可 性.加.经验证明,当试验进行的次数 n 很大时,事件 A 的频率 具有一定的稳定性:即当试验次数 充分大时,频率 f n (A) 总在一个确定的数字附近摆动 f n (A) n 例1 古代学者摩根(Morgan)、蒲丰(Buffon)和皮尔逊(Peason),分别做 了多次抛掷硬币的试验,观察正面出现的次数,记录结果如表1-1所示 .其中 是抛掷硬币的次数, 表示事件“出现正面”, 是在 次 试验中正面出现的次数, 表示 次试验中正面出现的频率. n H H n f n (H ) n n 表1-1 实验者 试验次数 正面出现次数 频率 摩 根 2048 1010 蒲 丰 2048 0.5069 皮尔逊 12000 6019 皮尔逊 24000 12012 0.5005 4040 0.5016 0.4932

从表1-1可以看到,当试验次数n很大以后,频 率fn()在0.5附近摆动,并逐渐稳定于0.5. 我们把频率,(A)围绕摆动的稳定值P,就叫做事件 A的概率,即有概率的统计定义如下: 2,概率的统计定义 定义2在相同的条件下重复进行n次试验,如果当n增大时, A事件的频率,()=”稳定地在某一常数p附近摆动, 则称常数P为事件A的概率,记P(A)三p 为根据这一定义,可以把由大量重复试验所得到的事件的频率作为事 件概率的近似值. 二、古典概型 1.等可能概型(也叫做古典概型):具有以下特点的试验称为 等可能概型: (①)只有有限个基本事件,即基本空间为有限空间, 2={01,023,0n};
从表1-1可以看到,当试验次数 很大以后,频 率 在0.5附近摆动,并逐渐稳定于0.5. n f (H ) n 我们把频率 围绕摆动的稳定值 ,就叫做事件 的概率,即有概率的统计定义如下: f (A) n p A 2.概率的统计定义 定义2 在相同的条件下重复进行 次试验,如果当 增大时, 事 件 的 频 率 n n A 稳 定 地 在 某 一 常 数 附近摆动, n n f A A n ( ) = p 则称常数 为事件 的概率,记 为 . p A P(A) = p 根据这一定义,可以把由大量重复试验所得到的事件的频率作为事 件概率的近似值. 二、古典概型 1.等可能概型(也叫做古典概型):具有以下特点的试验称为 等可能概型: (i) 只有有限个基本事件,即基本空间为有限空间, = {1 , 2 , , n };