
第二章随机变量及其分布 第一节随机变量及其分布函数 一、随机变量 用数量来表示试验的基本事件 定义1设试验E的基本空间为2,2={o),如果对试验E的每一个基 本事件0,规定一个实数记作X()与之对应,这样就得到一个定义在基本空 间2上的一个单值实函数X=X(o),称变量X=X(o)为随机变量. 随机变量常用字母X、Y、Z等表示.或用5、)等表示
第二章 随机变量及其分布 第一节 随机变量及其分布函数 一、随机变量 用数量来表示试验的基本事件 定义1 设试验 的基本空间为 , ,如果对试验 的每一个基 本事件 ,规定一个实数记作 与之对应,这样就得到一个定义在基本空 间 上的一个单值实函数 ,称变量 为随机变量. E = {} E X () X = X() X = X() 随机变量常用字母 X 、 Y 、 Z 等表示.或用 、 等表示.

注:1°随机变量X=X(o)是基本事件的函数, 具体间题里具体规定 2°对于不同的基本事件,X的取值亦要不同. 3°每一基本事件都可用随机变量的取值来表示.如X(®)=xk, 则Dk={X=Xk} 4°当xk≠X,时,事件{X=}与{X=x,}互不相容 5°{X≤x}表示X取小于等于x的每一个值所对应的基本事件的 和事件 二、随机变量的分布函数
注:1°随机变量 是基本事件的函数, 具体问题里具体规定. 2°对于不同的基本事件, 的取值亦要不同. 3°每一基本事件都可用随机变量的取值来表示.如 , 则 . 4°当 时,事件 与 互不相容. 5° 表示 取小于等于 的每一个值所对应的基本事件的 和事件 X = X() X k k X ( ) = x { } k k = X = x k r x x { }k X = x { }r X = x {X x} X x 二、随机变量的分布函数

定义2设X是一个随机变量,对任意实数X,令 F(x)=P(X<x),(-o<x<+o) 称F)为随机变量X的分布函数, 分布函数是定义在(一0,十©)上的函数.具有如下性质: 1°0≤F(x1且F(-o0)=0F(+o∞)=1 2°F(x)是单调不减函数. 3°F(x)是右连续的,即F(x)=Fx)· 4°对任意a<b,有
定义2 设 X 是一个随机变量,对任意实数 x ,令 F(x) = P{X x}, (− x +) 称 F(x) 为随机变量 X 的分布函数. 分布函数是定义在 (−,+) 上的函数.具有如下性质: 1° ≤ ≤1且 , . 2° 是单调不减函数. 3° 是右连续的,即 . 0 F(x) F(x) F(−) = 0 F(+) =1 F(x) F(x ) = F(x) + 4°对任意 a b ,有

P{a<X≤b}=F(b)-F(a) Pia<X<b:=F(b)-F(a)-PX=b P{a≤X≤b}=F(b-F(a)+P{X=a} 第二节离散型随机变量及其概率分布 一、离散型随机变量及其分布律 定义3设E是一个试验,X为E中的随机变量,如果X只取有限个 数值或可数无穷多个数值,则称X为离散型随机变量. 定义4分布律:PX=}=卫k,k=1,2,,即
{ } ( ) ( ) { }. { } ( ) ( ) { }. { } ( ) ( ). P a X b F b F a P X a P a X b F b F a P X b P a X b F b F a = − + = = − − = = − 第二节 离散型随机变量及其概率分布 定义3 设 E 是一个试验,X 为 E 中的随机变量,如果 X 只取有限个 数值或可数无穷多个数值,则称 X 为离散型随机变量. 一、离散型随机变量及其分布律 定义4 分布律:P{X = xk } = pk , k = 1, 2, … , 即

X X1 X2 P p1p2· Pk 例如抛硬币的试验 P 1/2 1/2 掷骰子的试验 X 2 3 4 5 6 P 1/61/61/61/61/61/6
X 1 x 2 x k x P 1 p 2 p k p … … … … 例如抛硬币的试验 X P 1/2 1/2 1 0 掷骰子的试验 X P 1/6 1/6 1/6 1/6 1/6 1/6 1 2 3 4 5 6

分布律的性质: 1°Pk0,k=1,2,; 2。 k= 例1某人射击命中率为p,不断地独立射击目标,直到命中为止, 求发射子弹数X的分布律(概率分布). 解X可取值为1,2,…,k,,{X=k表示事件“前k-1 次不中,第k次击中”,则P=PX=k;=I一p)p=gp ,因此 (q=1-p)
分布律的性质: 1° pk ≥0, k =1,2,…; 2° . = = 1 1 k pk 例1 某人射击命中率为 ,不断地独立射击目标,直到命中为止, 求发射子弹数 的分布律(概率分布). p X 解 可取值为1,2,…, ,…, 表示事件“前 次不中,第 次击中” ,则 . ,因此 X k {X = k} k −1 k p P X k p p q p k k k 1 1 { } (1 ) − − = = = − = (q =1− p)

2 p gp X 0 例2设 求X为分布函 F(x) P 1/2 1/2 数 F(x) 0 x<0 解 F(x) 1/2, 0≤x< 1 x≥1
X k P p qp q p 2 q p k−1 1 2 3 … … … … 例2 设 P 1/2 1/2 X 1 0 ,求 为分布函 数 . X F(x) 解 = 1, 1 1/ 2 , 0 1 0 , 0 ( ) x x x F x · · F(x) x 2 1 1 · 。 1 o
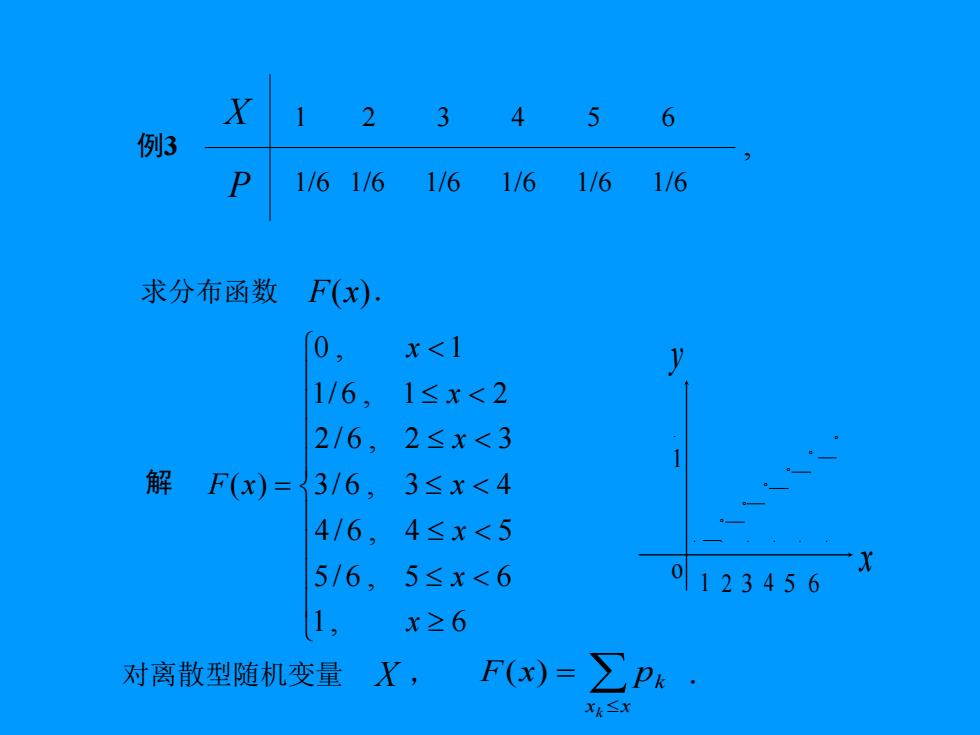
X 234 5 6 例3 1/61/6 1/6 1/6 116 1/6 求分布函数F(x). 0 x<] 1/6,1≤x<2 2/6,2≤x<3 解 F(x)=3/6, 3≤x≤4 4/6, 4≤x<5 5/6,5≤x<6 01123456 1 X≥6 对离散型随机变量X, F()=∑P
例3 , 1 2 3 4 5 6 1/6 1/6 1/6 1/6 1/6 1/6 X P 求分布函数 F(x). 解 = 1 , 6 5/ 6 , 5 6 4 / 6 , 4 5 3/ 6 , 3 4 2 / 6 , 2 3 1/ 6 , 1 2 0 , 1 ( ) x x x x x x x F x · · · · · · · y x 1 1 o 2 3 4 5 6 。 。 。 。 。 。 对离散型随机变量 X , . = x x k k F(x) p

二、几种常用的离散型随机变量及其概率分布 1.(0-1)分布 若随机变量X只取0与1两个值,其概率分布为 P{X=0}=1-p,P{X=1}=p,0<p< X 0 或写成PX=x}=p(①-p)P,x=01 1-p 则称X服从参数为P的(0-1)分布或两点分布 0 x<0 分布函数F(x) 1-p0≤x<1. x≥1
二、几种常用的离散型随机变量及其概率分布 1.(0-1)分布 若随机变量 X 只取0与1两个值,其概率分布为 P{X = 0}=1− p, P{X =1}= p, 0 p 1 或写成 { } (1 ) , 0,1 1 = = − = − P X x p p x x x 则称 X 服从参数为 p 的(0-1)分布或两点分布. 分布函数 − = 1, 1 1 , 0 1 0 , 0 ( ) x p x x F x . X 0 1 P 1-p p

2.二项分布 如果随机变量X的取值为0,1,2,…,n, 其分布律为 PX=k)= p1-p)-k,k=0,1,2,,n:0<p<1 则称X服从参数为n,p的二项分布,证作X~b(n,p) B(n,p) (或 当n=1时,二项分布BL,p)就是(0-1)分布. 在n重贝努利概型中,事件A发生的次数X就服从B(n,pP), p=P(A)
2.二项分布 如果随机变量 的取值为0,1,2,…, , 其分布律为 X n , 0,1,2,…, ; k n k p p k n P X k − − { = } = (1 ) k = n 0 p 1. 则称 服从参数为 , 的二项分布,证作 ~ (或 ). X n p X b(n, p) B(n, p) 当 =1时,二项分布 就是(0-1)分布. 在 重贝努利概型中,事件 发生的次数 就服从 , . n B(1, p) n A X B(n, p) p = P(A)