
课程概况 《线性代数》是工学类、管理类和经济类各专业本科生最重 要的基础课之一。它不仅是培养抽象思维能力、逻辑推理能力、 数学建模能力、运算能力与综合运用所学知识分析问题和解决问 题的能力的重要途径,还是学习后继课程以及参加具有选拔功能 的水平考试(如研究生入学考试)的必备基础。 本课程的主要工具是矩阵和初等变换的理论。其主要内容可 用下面的框图来表示。 2
2 课程概况 《线性代数》是工学类、管理类和经济类各专业本科生最重 要的基础课之一。它不仅是培养抽象思维能力、逻辑推理能力、 数学建模能力、运算能力与综合运用所学知识分析问题和解决问 题的能力的重要途径,还是学习后继课程以及参加具有选拔功能 的水平考试(如研究生入学考试)的必备基础。 本课程的主要工具是矩阵和初等变换的理论。其主要内容可 用下面的框图来表示
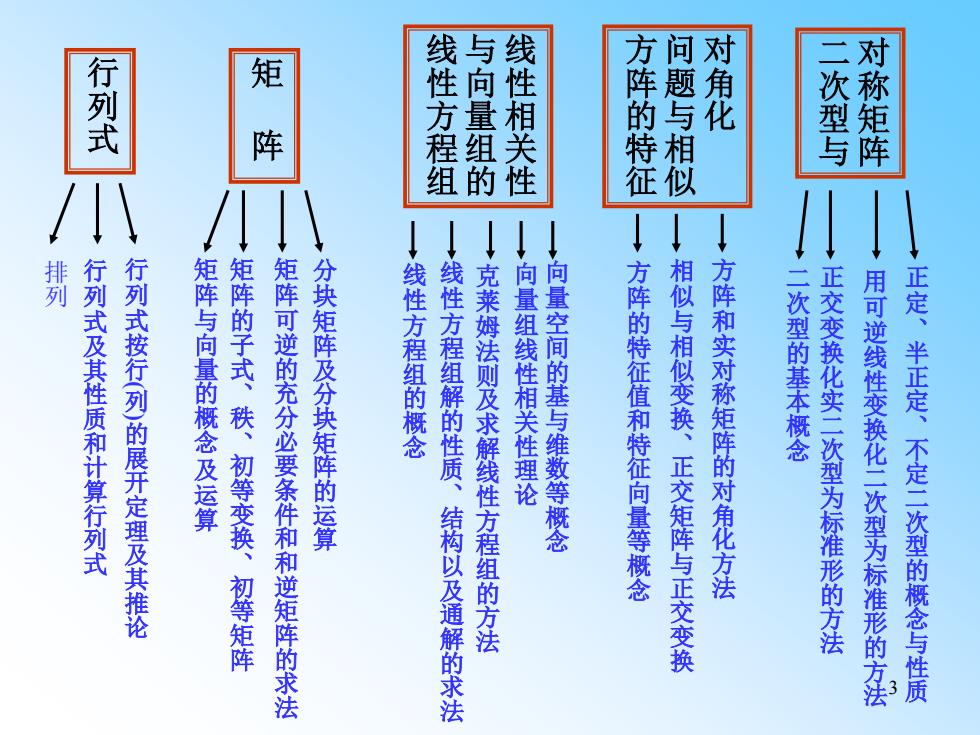
J对 行列式 矩 阵 线性方程组 与向量组 线性相关性 方阵的特征 问题与相似 鹿 二次型与 对称矩阵 排列 行列式及其性质和计算行列式 行列式按行列)的展开定理及其推论 矩阵与向量的概念及运算 矩阵的子式、秩、初等变换、 矩阵可逆的充分必要条件和和逆矩阵的求法 分块矩阵及分块矩阵的运算 线性方程组的概念 线性方程组解的性质、 克莱姆法则及求解线性方程组的方法 向量组线性相关性理论 向量空间的基与维数等概念 方阵的特征值和特征向量等概念 结构以及通解的求法 相似与相似变换、正交矩阵与正交变换 方阵和实对称矩阵的对角化方法 二次型的基本概念 正交变换化实二次型为标准形的方法 初等矩阵 用可逆线性变换化二次型为标准形的方法 正定、半正定、不定二次型的概念与性质
3 行列式 矩阵 矩阵与向量的概念及运算 矩阵的子式、秩、初等变换、初等矩阵 矩阵可逆的充分必要条件和和逆矩阵的求法 分块矩阵及分块矩阵的运算 线性相关性 与向量组的 线性方程组 线性方程组的概念 克莱姆法则及求解线性方程组的方法 向量组线性相关性理论 向量空间的基与维数等概念 线性方程组解的性质、结构以及通解的求法 对角化 问题与相似 方阵的特征方阵的特征值和特征向量等概念 相似与相似变换、正交矩阵与正交变换 方阵和实对称矩阵的对角化方法 对称矩阵 二次型与 二次型的基本概念 正交变换化实二次型为标准形的方法 用可逆线性变换化二次型为标准形的方法 正定、半正定、不定二次型的概念与性质 排列 行列式及其性质和计算行列式 行列式按行( 列) 的展开定理及其推论

第一章行列式 行列式是一种常用的数学工具,在数学和其他应用学科以及工 程技术中,有着广泛的应用。本章主要介绍行列式的概念、性质和 计算方法.为了研究行列式理论的需要,首先介绍排列的一些知识 第一节排列及其逆序数 前n个自然数1,2,…,n按照任何一种次序排成一列,称为这n 个数的一个全排列, 例如前三个自然数1,2,3的全排列共有31=6种不同的排法: 123,132,213,231,312,321。 定义1前n个自然数每一种有次序的全排列称为一个n级 排列,简称排列
4 第一节 排列及其逆序数 例如前三个自然数1,2,3的全排列共有3!=6种不同的排法: 123,132,213,231,312,321。 前 个自然数 按照任何一种次序排成一列,称为这 个数的一个全排列. n 1,2, ,n n 第一章 行 列 式 行列式是一种常用的数学工具,在数学和其他应用学科以及工 程技术中,有着广泛的应用.本章主要介绍行列式的概念、性质和 计算方法.为了研究行列式理论的需要,首先介绍排列的一些知识. 定义1 前 个自然数每一种有次序的全排列称为一个 级 排列,简称排列. n n

两个级排列,只要排在某个位置的对应数字不同(如123n 与213),就视为不同的排列.那么,排在第一个位置的数字 有种不同的排法,当第一个数字排定后,第二个位置的数字只有 n-1种不同的排法,依次下去,第n个位置的数字只有1种排法,由 此可知,所有不同的n级排列的总数为: n(n-1)…3·2.1=nl 按数字从小到大的顺序所产生的n级排列:l23…n称为顺序排 列或标准排列. 在一个非标准排列中,一定有某个大数排在小数之前的情况, 此时就说该排列出现了一个逆序.一个排列中所有逆序的总个数 称为该排列的逆序数 排列PP2…Pn的逆序数记为t(PP2…Pn) 逆序数为奇数的排列叫做奇排列,逆序数为偶数的排列叫做偶 排列
5 按数字从小到大的顺序所产生的 级排列: 称为顺序排 列或标准排列. n 123 n 两个 级排列,只要排在某个位置的对应数字不同(如 与 ),就视为不同的排列.那么,排在第一个位置的数字 有 种不同的排法,当第一个数字排定后,第二个位置的数字只有 种不同的排法,依次下去,第 个位置的数字只有1 种排法,由 此可知,所有不同的 级排列的总数为: n 123 n 213 n n n−1 n n n n n ( 1) 3 2 1 !. − = 在一个非标准排列中,一定有某个大数排在小数之前的情况, 此时就说该排列出现了一个逆序.一个排列中所有逆序的总个数 称为该排列的逆序数. 排列 p1 p2 pn 的逆序数记为 1 2 ( ). n p p p 逆序数为奇数的排列叫做奇排列,逆序数为偶数的排列叫做偶 排列.

例1判定下列排列的奇偶性(1)31542;(2)1726453。 解(1)这是一个五级排列,先求排列的逆序数.显然 x(31542)=0+1+0+1+3=5, 可见五级排列31542是一个奇排列。 (2)这是一个七级排列,求排列的逆序数,易知 (1726453)=0+0+1+1+2+2+4=10, 所以,七级排列1726453是一个偶排列。 定义2把一个排列中某两个数字的位置互相对调,称为对排列 的一次对换.特别地,相邻位置上两个数字的对换称为邻换. 对换和邻换都是对排列的运算,对排列进行一次对换或邻换, 排列的奇偶性必改变,即如果原来是奇排列,变为偶排列;如果原 来是偶排列,变为奇排列.为证明这一结论,有下面的定理和引理。 6
6 例1 判定下列排列的奇偶性(1)31542;(2)1726453。 定义2 把一个排列中某两个数字的位置互相对调,称为对排列 的一次对换.特别地,相邻位置上两个数字的对换称为邻换. 解(1)这是一个五级排列,先求排列的逆序数.显然 (31542) 0 1 0 1 3 5, = + + + + = 可见五级排列31542是一个奇排列。 (2)这是一个七级排列,求排列的逆序数,易知 (1726453)=0+0+1+1+2+2+4=10, 所以,七级排列1726453是一个偶排列。 对换和邻换都是对排列的运算,对排列进行一次对换或邻换, 排列的奇偶性必改变,即如果原来是奇排列,变为偶排列;如果原 来是偶排列,变为奇排列.为证明这一结论,有下面的定理和引理

引理一次邻换改变排列的奇偶性. 证不失一般性,设排列pP2…P,j9929:经一次邻换变为 P1P2…p,jiq192…93 ☒无法显示该图片。 卫P2…p,和q92…9,的各数字间的 相互位置以及它们分别与i或j的相互位置并无改变,因此它们的 逆序个数不变.由于i,j相互调换位置后,使排列 PP2…P,jiq92…9的逆序数比原来排列PP2…p,jq192…9 增1或减1,故排列P1P2…P,j992…9,与P1P2…Pjiq92…9的 奇偶性不同命题得证 7
7 1 2 1 2 s t p p p q q q 和 的各数字间的 相互位置以及它们分别与 或 的相互位置并无改变,因此它们的 逆序个数不变. i j 引理 一次邻换改变排列的奇偶性. 证 不失一般性,设排列 经一次邻换变为 1 2 1 2 , s t p p p jiq q q 1 2 1 2 s t p p p ijq q q 增1或减1, 故排列 与 的 奇偶性不同.命题得证 1 2 1 2 s t p p p ijq q q i j , 1 2 1 2 s t p p p jiq q q 由于 相互调换位置后,使排列 的逆序数比原来排列 1 2 1 2 s t p p p ijq q q 1 2 1 2 s t p p p jiq q q

定理1一次对换必改变排列的奇偶性. 证设排列 p1…pig…fmj91…9% (1)》 经一次对换化为排列 卫1…PJr…Tm1q19 (2) 根据引理,只要证明由(1)到(2)的一次对换可以经过奇 数次邻换来实现就可以了. 事实上,在排列(1)中将数字i依次向右做m+1次邻换, 得排列 p1…ph1mjiq1…9 再将上述排列中的数字j依次向左做m次邻换,得到的排列 即为(2). 总之,(1)可经2m+1)次邻换化为(2).证毕. 8
8 根据引理,只要证明由(1)到(2)的一次对换可以经过奇 数次邻换来实现就可以了. 事实上,在排列(1)中将数字 依次向右做 次邻换, 得排列 i m +1 l m qk p1 p r1 r jiq1 再将上述排列中的数字 依次向左做 次邻换,得到的排列 即为(2). j m 总之,(1)可经( 2m +1 )次邻换化为(2).证毕. 定理1 一次对换必改变排列的奇偶性. 证 设排列 (1) 经一次对换化为排列 (2) l m qk p1 p ir1 r jq1 l m qk p1 p jr1 r iq1

例2已知3口452☐为一个六级排列,将数字1和6填入口内,使 其成为奇排列 解我们可以将数字1和6随意填入两个口内,然后求此排列的 逆序数.如果逆序数是奇数,该排列即为所求;如果逆序数为偶 数,由定理1,将数字1和6的位置对调,便得所求的排列. 今将数字1填入第一个口内,将数字6填入第二个口内,得排列 314526,则该排列的逆序数为 x(314526)=0+1+0+0+3+0=4, 即排列314526为偶排列,由定理1,将数字1和6的位置对调,得 奇排列364521. 最后我们指出,本节讨论的前个自然数的排列问题可以推广 到任意n个不同元素的全排列中去, 9
9 由定理1,将数字1和6的位置对调,得 奇排列364521. 例2 已知3□452□为一个六级排列,将数字1和6填入□内,使 其成为奇排列. 解我们可以将数字1和6随意填入两个□内,然后求此排列的 逆序数.如果逆序数是奇数,该排列即为所求;如果逆序数为偶 数,由定理1,将数字1和6的位置对调,便得所求的排列. 今将数字1填入第一个□内,将数字6填入第二个□内,得排列 314526,则该排列的逆序数为 (314526) 0 1 0 0 3 0 4, = + + + + + = 即排列314526为偶排列, 最后我们指出, 本节讨论的前 n 个自然数的排列问题可以推广 到任意 n 个不同元素的全排列中去
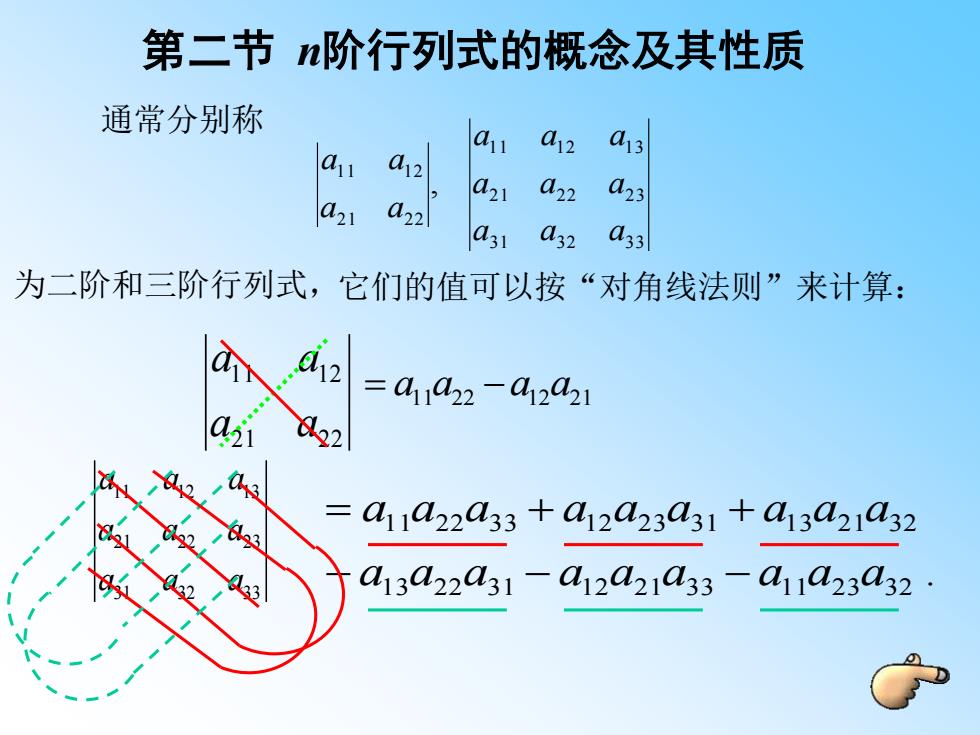
第二节n阶行列式的概念及其性质 通常分别称 412a413 a21 a22 a23 a21 22 a31 43233 为二阶和三阶行列式,它们的值可以按“对角线法则”来计算: =411422-412421 2 = 411022a33+a12a23a31+413Q21032 013022031-a12021a33-a11023032 ①
11 11 12 13 21 22 23 31 32 33 a a a a a a a a a 第二节 n阶行列式的概念及其性质 它们的值可以按“对角线法则”来计算: 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 2 1 2 2 1 1 1 2 , a a a a a a a a a a a a a 为二阶和三阶行列式, 通常分别称 . 1 3 2 2 3 1 1 2 2 1 3 3 1 1 2 3 3 2 1 1 2 2 3 3 1 2 2 3 3 1 1 3 2 1 3 2 a a a a a a a a a a a a a a a a a a − − − = + + 21 22 11 12 a a a a = a11a22 −a12a21

定义3将n2个数 a(i,j=1,2,…,n) 排成如下形式 412 ain a21 2 (3) am an2 ar 称为一个阶行列式.“|”是行列式的记号.行列式中每个横排 称为一行,每个竖排称为一列,数a,称为该行列式的第行第j列 的元素,i和j分别称为元素a,的行标和列标. ★ 定义4n阶行列式(3)中取自不同行又不同列的n个元素的乘 积aaan称为该行列式的一个均匀分布乘积项,简称为均布项 排列i2…in称为它的行标排列,j2…j称为它的列标排列. 我们规定:一个均布项中诸元素互换位置得到的所有均布项都 视为同一个均布项, 12
12 定义3 将 n 2 个数 a i j n ij ( , 1,2, , ) = 排成如下形式 11 12 1 21 22 2 1 2 (3) n n n n nn a a a a a a a a a 积 称为该行列式的一个均匀分布乘积项,简称为均布项. 定义4 n 阶行列式(3)中取自不同行又不同列的 n 个元素的乘 n n ai j ai j ai j 1 1 2 2 排列 i 1 i 2 i n 称为它的行标排列, j 1 j 2 j n 称为它的列标排列. 我们规定:一个均布项中诸元素互换位置得到的所有均布项都 视为同一个均布项. 称为一个 阶行列式.“| |”是行列式的记号.行列式中每个横排 称为一行,每个竖排称为一列,数 称为该行列式的第 行第 列 的元素, 和 分别称为 元素 的行标和列标. n ij a i j i j aij