
上讲提要 1.定积分的概念、性质; 2.积分上限函数及其导数; 3.Newton-Leibniz公式。 3
3 上讲提要 1.定积分的概念、性质; 2.积分上限函数及其导数; 3.Newton-Leibniz公式

第二节定积分 三、Newton-Leibnize公式 函数f(x)在[a,b]上连续,且F'(x)=f(x),则 if达=F=F-F(a 四、定积分的计算 1.直接积分法 利用代数恒等变换或三角恒等变换,以及定积分的 性质,将定积分化为若干个易求的定积分之和,这种定 积分的计算方法称为直接积分法。 4
4 第二节 定积分 三、Newton-Leibnize 公式 函数 f x( )在[ , ] a b 上连续,且F x f x ( ) ( ) = ,则 ( ) ( ) ( ) ( ) b a b f x dx F x F b F a a = = − 四、定积分的计算 1.直接积分法 利用代数恒等变换或三角恒等变换,以 及定积分的 性质,将定积分化为若干个易求的定积分之和,这种定 积分的计算方法称为直接积分法
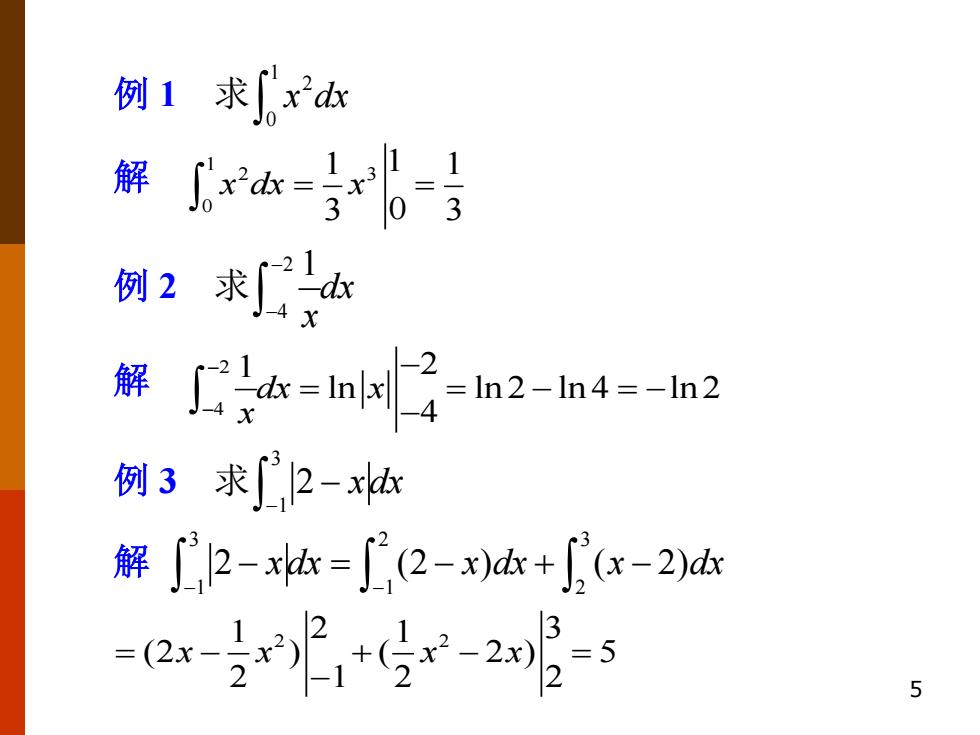
例1求∫xd 解 例2求 解 =la子 In2-In4=-In2 例3求2-x 解」2-x=∫2-x)dk+x-2)dk =2x21+-2-5 5
5 例 1 求 1 2 0 x dx 解 1 2 3 0 1 1 1 3 3 0 x dx x = = 例 2 求 2 4 1 dx x − − 解 2 4 1 2 ln ln 2 ln 4 ln 2 4 dx x x − − − = = − = − − 例 3 求 3 1 2 x dx − − 解 3 2 3 1 1 2 2 (2 ) ( 2) x dx x dx x dx − − − = − + − 2 2 1 1 2 3 (2 ) ( 2 ) 5 2 2 1 2 = − + − = x x x x −

例4求 2 2 解 sn0-oswa π1 例5求 1+ 解 4xs--1+a --.:)61 6
6 例 4 求 2 2 0 sin 2 x dx 解 2 2 2 0 0 1 sin (1 cos ) 2 2 x dx x dx = − 2 0 1 1 ( sin ) 2 4 2 x x = − = − 例 5 求 2 1 2 0 1 x dx + x 解 2 1 1 2 2 0 0 1 (1 ) 1 1 x dx dx x x = − + + 1 ( arctan ) 1 0 4 x x = − = −

例6求∫tan2xdx 解tan'xdx=∫在(sc2x-1)d (tanx-x)4 =1- 0 2.换元积分法 公式设函数f(x)在[a,b]上连续,而x=p(t)在区间[,] 或[B,o]上单值且有连续导数,当t在[α,B]或[B,]上变 化时,x在[a,b]上变化,且p(a)=,p(b)=B,则 2fax)ak=「2foup'u)dt 7
7 例 6 求 4 2 0 tan xdx 解 4 4 2 2 0 0 tan (sec 1) xdx x dx = − (tan ) 1 4 4 0 x x = − = − 2.换元积分法 公式 设函数 f x( )在[a,b]上连续,而x t =( )在区间[ , ] 或[ , ] 上单值且有连续导数,当 t 在[ , ] 或[ , ] 上变 化时,x 在[a,b]上变化,且 ( ) , ( ) a b = = ,则 ( ) ( ( )) ( ) b a f x dx f t t dt =

上式反过来看,∫fo(x)()=fuh为凑分法公 式。 例1求(x2+1xd 解r+=2cx+x+1y达 令x2+1=t,x=0,t=1,x=1,t=2 er+h-rh=g-点 或刘ra2+广ar--gr+r6 8
8 上 式反过来看, ( ( )) ( ) ( ) b a f x x dx f t dt = 为凑分法公 式。 例 1 求 1 2 3 0 ( 1) x xdx + 解 1 1 2 3 2 3 2 0 0 1 ( 1) ( 1) ( 1) 2 x xdx x x dx + = + + 令 2 x t x t x t + = = = = = 1 , 0, 1; 1, 2 1 2 2 3 3 4 0 1 1 1 15 2 ( 1) 2 8 8 1 x xdx t dt t + = = = 或 1 1 2 3 2 3 2 2 4 0 0 1 1 15 1 ( 1) ( 1) ( 1) ( 1) 2 8 8 0 x xdx x d x x + = + + = + =
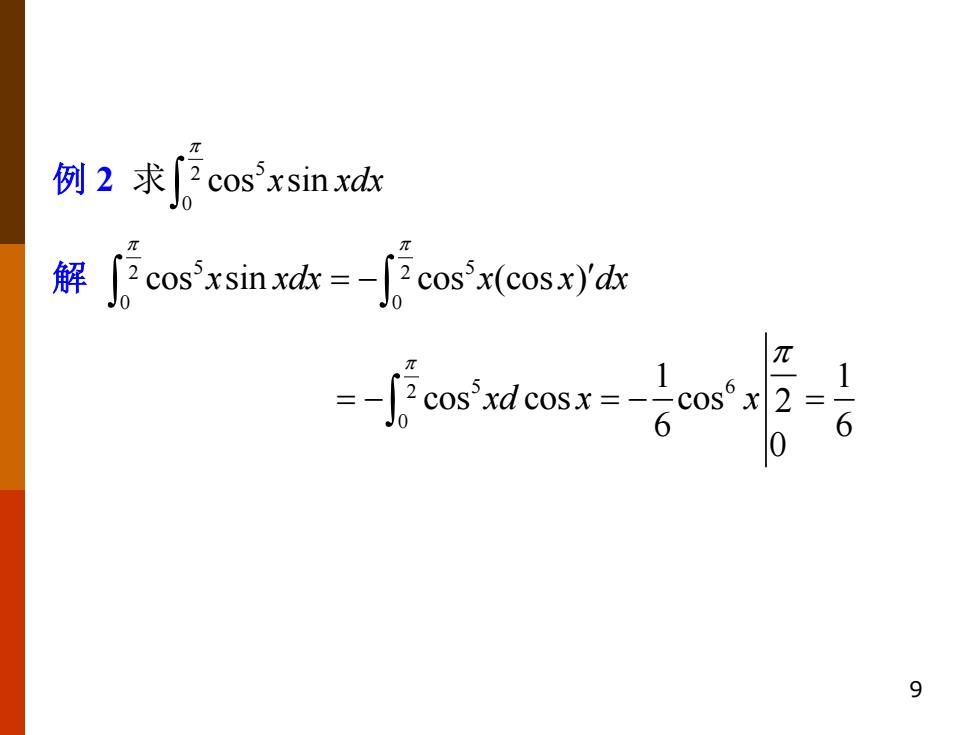
例2求2 cos'xsin xdx cos'xsinxdcos(cos x) -2 1-6 0 9
9 例 2 求 2 5 0 cos sin x xdx 解 2 2 5 5 0 0 cos sin cos (cos ) x xdx x x dx = − 2 5 6 0 1 1 cos cos cos 2 6 6 0 xd x x = − = − =
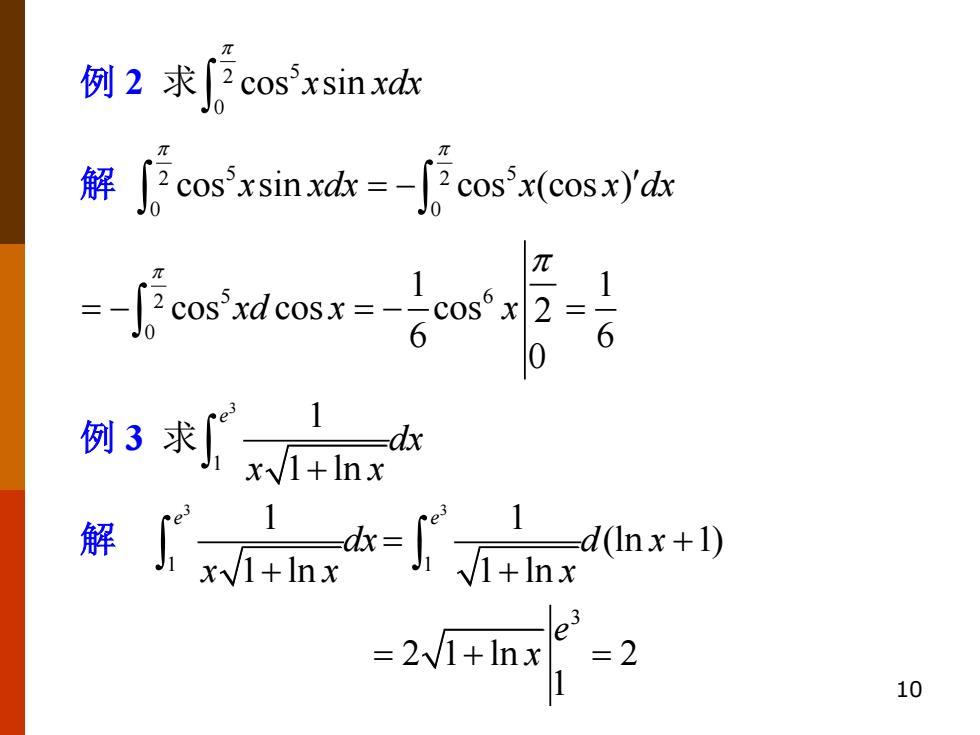
例2求∫2 cos'xsinxdx [cos'xsin xdx=-[cosx(cosx)dx 2eo8 dcos6ow✉38 解了中n=矿i nx) =2v1+Inx 10
10 例 2 求 2 5 0 cos sin x xdx 解 2 2 5 5 0 0 cos sin cos (cos ) x xdx x x dx = − 2 5 6 0 1 1 cos cos cos 2 6 6 0 xd x x = − = − = 例 3 求 3 1 1 1 ln e dx x x + 解 3 1 1 1 ln e dx x x + 3 1 1 (ln 1) 1 ln e d x x = + + 3 2 1 ln 2 1 e = + = x

例4求x2V1-x2 解 =sint,dx=cosidix=0.-0:x=1,= π d=sin't-sin'icostdt sin'tcos disin2dr ddcos4rd 4J0 π (t 8 -4sn42)= 2 4 16 11
11 例 4 求 1 2 2 0 x x dx 1− 解 令 sin , cos , 0, 0; 1, 2 x t dx tdt x t x t = = = = = = 1 2 2 2 2 2 0 0 x x dx t t tdt 1 sin 1 sin cos − = − 2 2 2 2 2 0 0 1 sin cos sin 2 4 t tdt tdt = = 2 2 2 0 0 0 1 1 cos4 1[ cos4 ] 4 2 8 t dt dt tdt − = = − 1 1 ( sin 4 ) 2 2 8 4 16 0 0 t t = − =

dx J01+√ 解 x=1,x=12,dx=2tdt,x=0,t=0x=1,1=1 -12 -2u-1+M =2-4nl:0日 =2ln2-1 12
12 例 5 求 1 0 1 x dx + x 解 令 2 x t x t dx tdt x t x t = = = = = = = , , 2 , 0, 0; 1, 1 1 1 0 0 2 1 1 x t dx tdt x t = + + 2 1 0 1 1 2 1 t tdt t − + = + 1 0 1 2 ( 1 ) 1 t dt t = − + + 2 1 1 2( ln 1 ) 2 0 = − + + t t t = − 2ln 2 1