
上讲提要 1.导数的概念、几何意义、物理 意义; 2.可导与连续的关系; 3.导数的四则运算 。 3
3 上讲提要 1.导数的概念、几何意义、物理 意义; 2.可导与连续的关系; 3.导数的四则运算

第二节 初等函数的导数 三、反函数的求导法则 定理2-1若函数x=p(y)在y点的某邻域内单调,可导, 且p'(y)≠0,则它的反函数y=f(x)在x点(x=p(y)处可 导,且 f(x)=1 p'(y) 简单地说,反函数的导数等于直接函数的导数的倒数。 例1已知y=aresin(-10,故在(-1,1)内有
4 第二节 初等函数的导数 定理2-1 若函数 x y = ( )在 y 点的某邻域内单调,可导, 且 ( ) 0 y ,则它的反函数 y f x = ( )在x点( x y = ( ))处 可 导,且 1 ( ) ( ) f x y = 简单地说,反函数的导数等于直接函数的导数的倒数。 三、反函数的求导法则 例1 已知 y x = arcsin ( 1 1, ) 2 2 x y − − ,求 y 。 解 y x = arcsin 是x y = sin 的反函数。x y = sin 在( , ) 2 2 − 单调、可导,且(sin ) cos 0 y y = ,故在( 1,1) − 内有
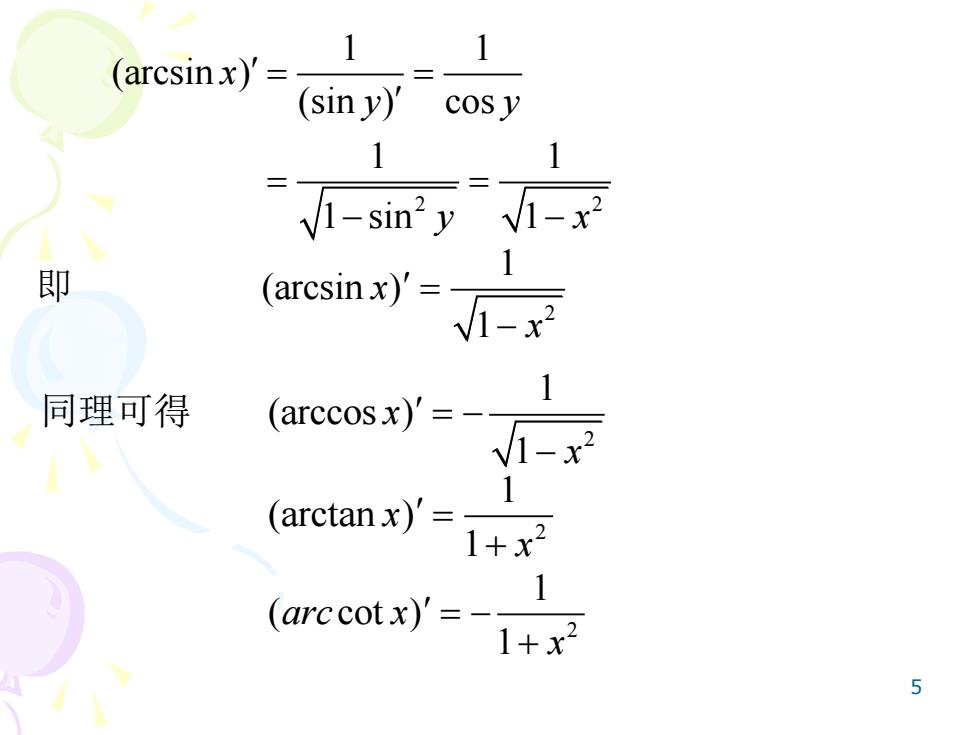
1 (arcsinx)'= (siny)' cos v 1 1-sin2y v1-x2 即 (arcsinx) 1-x 同理可得 (arccosx)'=-- 1 1-x2 (arctanx)= (arccotx)'=- 1 +x2 5
5 2 2 1 1 (arcsin ) (sin ) cos 1 1 1 sin 1 x y y y x = = = = − − 即 2 1 (arcsin ) 1 x x = − 同理可得 2 1 (arccos ) 1 x x = − − 2 1 (arctan ) 1 x x = + 2 1 ( cot ) 1 arc x x = − +

例2已知y=a(a>0且a≠1),求y'。 解已知y=a是x=loga y的反函数, 而x=log。y在(0,+o)上单调可导,且 (log。yy= ≠0 ylna 故在相应的区间(-0,+0)内,有 (a)y= ylna=a*Ina (log,y)' 即 (a")'=a"Ina 特别,a=e时,有 (e)'=e。 四、复合函数的求导法则 定理2-2(锁链法则)设函数u=0(x)在x点处可导,而函数
6 例2 已知 x y a = ( a 0且a 1 ),求 y 。 解 已知 x y a = 是 loga x y = 的反函数, 而 loga x y = 在(0, ) + 上单调可导,且 1 (log ) 0 ln a y y a = 故在相应的区间( , ) − + 内,有 1 ( ) ln ln (log ) x x a a y a a a y = = = 即 ( ) ln x x a a a = 特别,a e = 时,有 ( ) x x e e = 。 四、复合函数的求导法则 定理 2-2 (锁链法则)设函数u x = ( )在x点处可导,而函数

y=f(u)在x点对应的u(u=p(x)点处可导,则复合函数 y=f(p(x)在x点处可导,且其导数为 [f(p(x)]'=f'(wW)p'(x) 或 dydy du dx du dx 证明给x一增量△x,则相应地有函数u=p(x)的增量 △u,函数y的增量△y。己知函数y=f()在u点可导,则有 lim Ay=f'(u)(Au≠0) Au-→0△W 故 y =f'(w0+a △u 其中lim a=0, △1M->0 7
7 y f u = ( )在 x 点对应的 u u x ( ( )) = 点处可导,则复合函数 y f x = ( ( )) 在x点处可导,且其导数为 [ ( ( ))] ( ) ( ) f x f u x = 或 dy dy du dx du dx = 证 明 给 x 一增量x ,则相应地有函数 u x = ( )的增量 u,函数y的增量y 。已知函数y f u = ( )在u点可导,则有 0 lim ( ) u y f u → u = ( u 0) 故 ( ) y f u u = + 其中 0 lim 0 u → =

即 △y=f'(u)△u+0△w △x≠0时, 少y=f'( △x ’△x △x 由于u=p(x)在x点可导,故u在x点连 续,所以当△x→0时, △u=p(x+△x)-p(x)-→>0 故lim Av=M(u)lim Aulim alim u-f(u)() △x→0△x Ar→0△X△u→0Ar→0△X 即 [f(p(x)]'=f'(u)p'(x)。 此定理可以推广以任意有限个函数复合情形。例 如:v=yw(x)在x点可导,M=p(v)在x点的对应点 v(v=w(x)可导,y=f4又在v点的对应点u(u=p(v)可导
8 即 = + y f u u u ( ) x 0时, ( ) y u u f u x x x = + 由于u x = ( )在x点可导,故u在x点连 续,所以当 →x 0时, = + − → u x x x ( ) ( ) 0 故 0 0 0 0 lim ( ) lim lim lim x x u x y u u f u x x x → → → → = + = f u x ( ) ( ) 即 [ ( ( ))] ( ) ( ) f x f u x = 。 此定理可以推广以任意有限个函数复合情形。例 如 : v x = ( ) 在 x 点可导, u v = ( ) 在 x 点的对应点 v(v x = ( ))可导,y f u = ( )又在v点的对应点u( ( ) u v = )可导

则复合函数f{p[y(x)}在x点可导,且导数为 (f{p[yw(x)]})'=f'()p'(v)w'(x) 或 dy dy du dv dx du dy dx 例1.已知y=cos2x,求。y 解 令y=cosu,u=2x,则有 (cosu)(2.--sinu-2=-2sim2x du dx 例2己知y=(x3-sinx)4,求y'。 解令y=w,u=x3-sinx,则有 yu=(uy(x'-sinxy=4u(3x-cosx) du dx =4(x3-sinx)3(3x2-cosx) 9
9 则 复 合 函 数 f x { [ ( )]} 在 x 点 可 导 , 且 导 数 为 ( { [ ( )]}) ( ) ( ) ( ) f x f u v x = 或 dy dy du dv dx du dv dx = 例1.已知 y x = cos 2 ,求。 y 解 令y u u x = = cos , 2 ,则有 (cos ) (2 ) sin 2 2sin 2 dy du y u x u x du dx = = = − = − 例2 已知 3 4 y x x = − ( sin ) ,求 y 。 解 令 4 3 y u u x x = = − , sin ,则有 4 3 3 2 ( ) ( sin ) 4 (3 cos ) dy du y u x x u x x du dx = = − = − 3 3 2 = − − 4( sin ) (3 cos ) x x x x
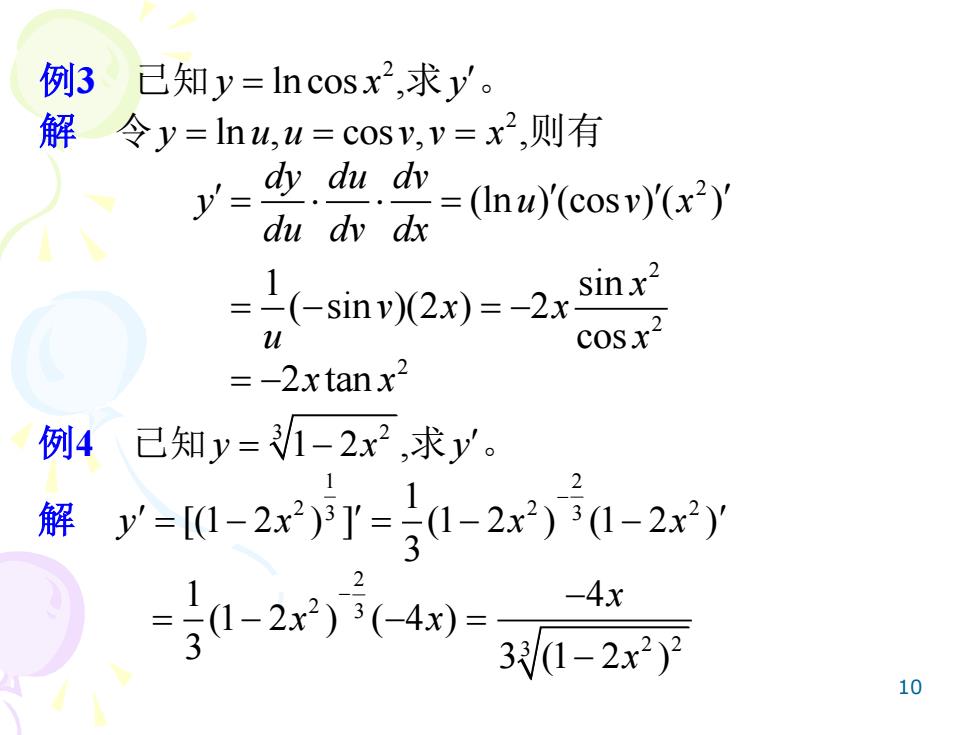
例3已知y=Incosx2,求y'。 解令y=lnw,w=cosy,v=x2,则有 u=(m(cosv( du dy dx -(-snvX2x)=-2rsin Cosx2 =-2xtanx2 例4已知y=1-2x2,求y。 解y=[1-2x2)5Y=0-2x)50-2xy 0-2x)(-4) -4x 3/1-2x2)2 10
10 例3 已知 2 y x = ln cos ,求 y 。 解 令 2 y u u v v x = = = ln , cos , ,则有 2 2 2 (ln ) (cos ) ( ) 1 sin ( sin )(2 ) 2 cos dy du dv y u v x du dv dx x v x x u x = = = − = − 2 = −2 tan x x 例4 已知 3 2 y x = −1 2 ,求 y 。 解 1 2 2 2 2 3 3 1 [(1 2 ) ] (1 2 ) (1 2 ) 3 y x x x − = − = − − 2 2 3 3 2 2 1 4 (1 2 ) ( 4 ) 3 3 (1 2 ) x x x x − − = − − = −

例5已知y=x(a为实数),求y 解y=(ealnx)=enx(@lnx')=x“au'=axa- X 例6已知函数y=xnx,求y'。 解y=(emn)=emn((sinInx)) =xsImx[(sinx)'Inx+sinx(Inx)] x[cosxln+sin] X 例7已知y=sin3x+cos2x,求y'。 y'=(sin3x+cos2x)'=(sin3x)'+(cos2 x)' cos3x(3x)+2cosx(cosx)=3cos3x-2cosxsinx =3cos 3x-sin 2x 11
11 例5 已知 y x = ( 为实数),求 y 解 ln ln 1 ( ) ( ln ) x x y e e x x x = = = 1 x − = 例6 已知函数 sin x y x = ,求 y 。 解 ( ) sin ln sin ln (sin ln ) x x x x y e e x = = sin [(sin ) ln sin (ln ) ] x = + x x x x x sin sin [cos ln ] x x x x x x = + 例7 已知 2 y x x = + sin3 cos ,求 y 。 解 y = 2 2 (sin3 cos ) (sin3 ) (cos ) x x x x + = + = + = − cos3 (3 ) 2cos (cos ) 3cos3 2cos sin x x x x x x x = − 3cos3 sin 2 x x

例8.已知y=sin2 x Insinx,求y'。 解 y=(sin2xInsinx)' =(sin2x)'Insinx+sin2x(Insinx) -cos2x.2.Insinx+sin 2x-cosx sinx =2cos2x Insinx+2cos2x 例9.己=acn空+4-F,求y. y=(xarcsin'+(4-x' 12
12 例8.已知 y x x = sin 2 ln sin ,求 y 。 解 y x x = (sin2 lnsin ) = + (sin2 ) lnsin sin2 (lnsin ) x x x x 1 cos 2 2 ln sin sin 2 cos sin x x x x x = + 2 = + 2cos2 lnsin 2cos x x x 例9.已知 2 arcsin 4 2 x y x x = + − ,求 y 。 解 2 ( arcsin ) ( 4 ) 2 x y x x = + − 2 2 2 1 1 ( ) arcsin (4 ) 2 2 2 4 1 2 x x x x x x x = + + − − −