吉林大学：《高等数学》课程电子教案（PPT课件）第二章 一元函数微分学 §1 导数的概念

第二章 导数思想最早由法国 数学家Ferma在研究 一元品数微劣学 极值问题中提出， 微积分学的创始人： 英国数学家Newton 德国数学家Leibniz 导数一 描述函数变化快慢 微分学 微分一 描述函数变化程度 都是描述物质运动的工具（从微观上研究函数）

第二章 微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数) 一元函数微分学 导数思想最早由法国 数学家 Ferma 在研究 极值问题中提出. 英国数学家 Newton

第二章 §1导款的烧念 一、 引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、单侧导数 HIGH EDUCATION PRESS 机动 上 下页 返回 结束

一、引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、单侧导数 机动 目录 上页 下页 返回 结束 §1 导数的概念 第二章

一、引例 1.变速直线运动的速度 设描述质点运动位置的函数为 s=f(t) 则t到t的平均速度为 f(t)-f(to) 自由落体运动 t-to 8=5gr2 而在t,时刻的瞬时速度为 f(to) y lim f(t)-f(to) t→to t-to HIGH EDUCATION PRESS 机动 上页 下页 返回 结束

一、 引例 1. 变速直线运动的速度 设描述质点运动位置的函数为 s  f (t) 0 t 则t0到 t 的平均速度为 v  ( ) ( ) 0 f t  f t 0 t  t 而在 t0时刻的瞬时速度为 lim 0 t t v   ( ) ( ) 0 f t  f t 0 t  t 2 2 1 s  gt s o ( )0 f t f (t) t 自由落体运动 机动 目录 上页 下页 返回 结束

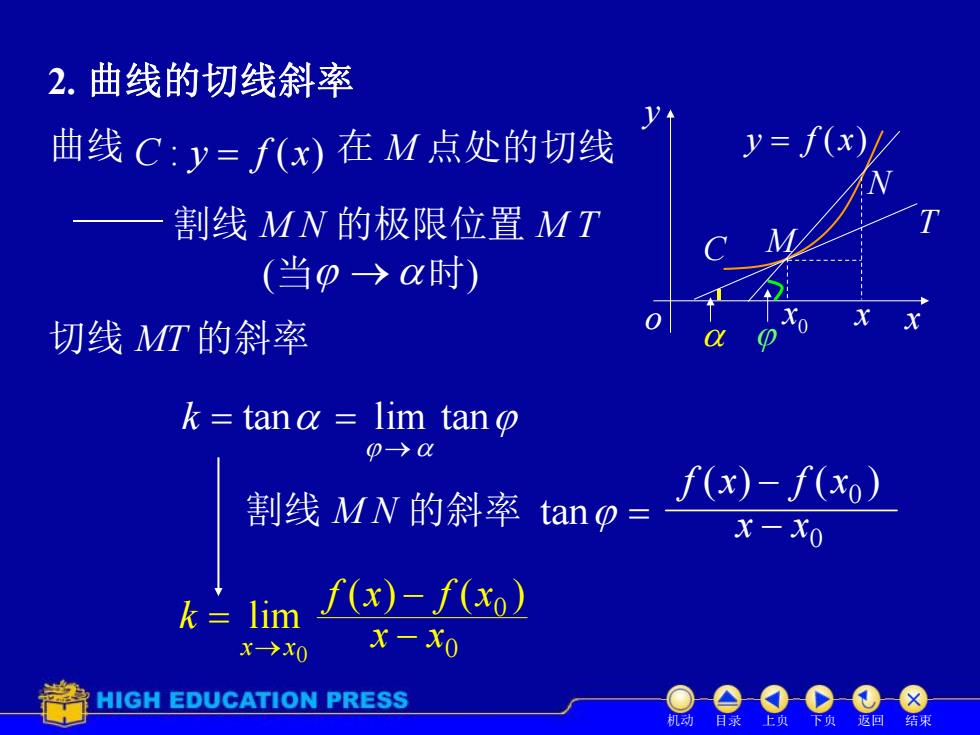
2.曲线的切线斜率 曲线C:y=f(x)在M点处的切线 y=f(x)/ 割线MN的极限位置MT (当0→时) 切线MT的斜率 k tana lim tan 0→ 割线MN的斜率 f(x)-f(x,) tano x-X0 k之lim f(x)-f(xo) x→x0 x-x0 HIGH EDUCATION PRESS 机动 目录 上页 下贞返回 结束

x y o y  f (x) C 2. 曲线的切线斜率 曲线 C : y  f (x)   N T 0 x M 在 M 点处的切线 x 割线 M N 的极限位置 M T (当  时) 割线 M N 的斜率 tan  ( ) ( ) 0 f x  f x 0 x  x 切线 MT 的斜率 k  tan    lim tan   lim 0 x x k   ( ) ( ) 0 f x  f x 0 x  x 机动 目录 上页 下页 返回 结束

f(】 瞬时速度y=lim f(t)-f(to) t→t0 t-to y=f(x) 切线斜率k=lim f(x)-f(xo) x→x0 x-X0 两个问题的共性： X 所求量为函数增量与自变量增量之比的极限 类似问题还有： 加速度是速度增量与时间增量之比的极限 角速度是转角增量与时间增量之比的极限 线密度是质量增量与长度增量之比的极限 变化率问题 电流强度是电量增量与时间增量之比的极限 HIGH EDUCATION PRESS 机动 返回 结束

两个问题的共性: s o 0 t ( ) 0 f t f (t) 瞬时速度 t lim 0 t t v   ( ) ( ) 0 f t  f t 0 t  t 切线斜率 x y o y  f (x) C   N T 0 x M x lim 0 x x k   ( ) ( ) 0 f x  f x 0 x  x 所求量为函数增量与自变量增量之比的极限 . 类似问题还有: 加速度 角速度 线密度 电流强度 是速度增量与时间增量之比的极限 是转角增量与时间增量之比的极限 是质量增量与长度增量之比的极限 是电量增量与时间增量之比的极限 变 化 率 问 题 机动 目录 上页 下页 返回 结束 

二、导数的定义 定义1.设函数y=f(x)在点x,的某邻域内有定义， 若 lim f(x)-f(xo) lim △y △y=f(x)-f(x) x→x0 x-x0 △x-→0△x △x=X-X0 存在，则称函数(x)在点x处可导， 并称此极限为 y=f(x)在点x,的导数记作 dy y=;'o df(x) dx=xo dx =xo 即 yx=o=f(xo)=lm Ay △x→0△X lim f(xo+△x)-f(xo) lim f(xo+h)-f(xo) △x→0 △X h-→0 HIGH EDUCATION PRESS 机动 返回 结束

二、导数的定义 定义1 . 设函数 y  f (x) 在点 0 x 0 lim xx 0 0 ( ) ( ) x x f x f x   x y x     0 lim ( ) ( ) 0 y  f x  f x 0  x  x  x 存在, f (x) 并称此极限为 y  f (x) 记作: ; 0 x x y   ( ) ; 0 f  x ; d d 0 x x x y  d 0 d ( ) x x x f x  即 0 x x y   ( ) 0  f  x x y x     0 lim x f x x f x x        ( ) ( ) lim 0 0 0 h f x h f x h ( ) ( ) lim 0 0 0     则称函数 若 的某邻域内有定义 , 在点 0 x 处可导, 在点 0 x 的导数. 机动 目录 上页 下页 返回 结束

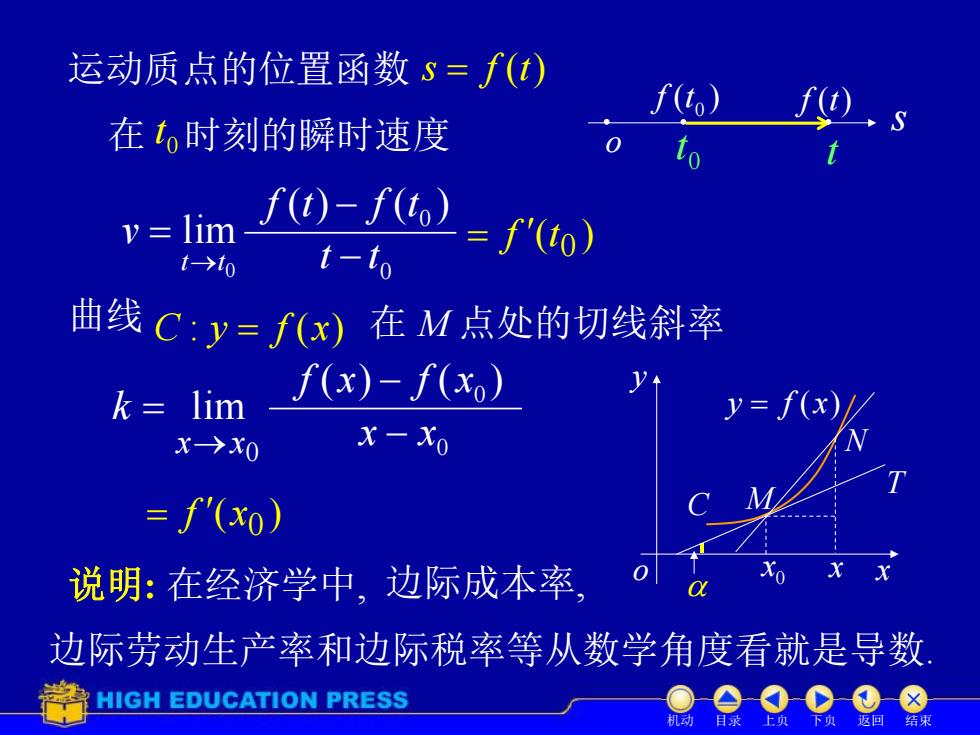
运动质点的位置函数s=f(t) f(t)■ 在t。时刻的瞬时速度 to v lim f()-f() t-to =f'(t0) t->to 曲线C:y=f(x)在M点处的切线斜率 =lim f(x)-f(xo) y=f(x)/ x→x0 x-Xo f(xo) 说明：在经济学中，边际成本率 Xo xx 边际劳动生产率和边际税率等从数学角度看就是导数 HIGH EDUCATION PRESS 机动 目录 上功 下贞返回 结束

运动质点的位置函数 s  f (t) s o 0 t ( ) 0 f t f (t) 在 时刻的瞬时速度 t 0 t lim 0 t t v   ( ) ( ) 0 f t  f t 0 t  t 曲线 C : y  f (x) 在 M 点处的切线斜率 x y o y  f (x) C  N T 0 x M x lim 0 x x k   ( ) ( ) 0 f x  f x 0 x  x ( ) 0  f  t ( ) 0  f  x 说明: 在经济学中, 边际成本率, 边际劳动生产率和边际税率等从数学角度看就是导数. 机动 目录 上页 下页 返回 结束

lim f(x)-f(xo) lim Ay △y=f(x)-f(x） x→X0 x-Xo △x→>0△X △X=x-X0 若上述极限不存在，就说函数在点x不可导 若1imy=o,也称f(x)在，的导数为无穷大 △x>0△X 若函数在开区间I内每点都可导，就称函数在1内可导 此时导数值构成的新函数称为导函数， 记作：y;f'(x); dy. df(x) dx dx 注意 八()=(xk=≠ f(xo) dx HIGH EDUCATION PRESS 机动 上 下贞返回 结束

0 lim xx 0 0 ( ) ( ) x x f x f x   x y x     0 lim ( ) ( ) 0 y  f x  f x 0  x  x  x 若上述极限不存在 , 在点 不可导. 0 x 若 lim , 0       x y x 也称 f (x) 在 0 x 若函数在开区间 I 内每点都可导, 此时导数值构成的新函数称为导函数. 记作: y ; f (x) ; ; d d x y . d d ( ) x f x 注意: ( ) 0 f  x 0 ( ) x x f x    x f x d d ( ) 0  就说函数 就称函数在 I 内可导. 的导数为无穷大 . 机动 目录 上页 下页 返回 结束

在导数的定义中，虽然x可以取区间内的任何数值， 但在极限的过程中，x是常量，△x或h是变量。 函数x)在点x处的导数f'(x)就是导函数f'(x)在点 x=x处的函数值，即 f()=f(x)x 例1.求函数f(x)=C(C为常数)的导数 解：y'=lim f(x+△x)-f(x) lim C-C =0 △x→0 △x △x-→0 △X 即 (C)y=0 HIGH EDUCATION PRESS

在导数的定义中，虽然x可以取区间I内的任何数值， 但在极限的过程中，x是常量，△x或h是变量。 函数f(x)在点x0处的导数 ( ) 0 f  x 就是导函数 f ′ (x) 在点 x=x0处的函数值，即 0 ( ) ' f x  0 ( ) | . ' x=x f x  例1. 求函数 f (x)  C (C 为常数) 的导数. 解: y  x C C x     0 lim  0 即 (C )  0 x f x x f x  (   )  ( ) 0 lim    x

例2求函数x)=(a>0,a≠1)的导数 解：f(x)=lim f(x+h)-f(x) lim axh-ax h→0 h -0 lim a(@"-D=alim-1 a'Ina. h->0 h h>0 这就是指数函数的导数公式.特殊地，当a=e时，因1ne=1, 故有 (e)'=e 例3求函数f(x)=x”(n∈N)在x=a处的导数 解：f'(a)=lim f(x)-f@=limx”-a x→a x-a x→ax-a =lim(x"-+ax-2+a2xn-3+…+a-） X→a nan-l HIGH EDUCATION PRESS 机动 上贞 返回 结束

例3 求函数 ( ) ( N )  f x  x n n 在x  a处的导数. 解: x a f x f a  ( )  ( ) xa f (a)  lim x a x a n n x a     lim lim( xa  n1 x 2  n a x 2 3  n a x  ) 1  n a 1  n n a 机动 目录 上页 下页 返回 结束 例2 求函数f(x)=a x(a＞0,a≠1)的导数. 解： 0 ( ) ( ) ( ) lim ' h f x+h f x f x  h   0 lim x+h x h a a  h 0 ( 1) lim x h h a a  h   0 1 lim h x h a a  h  ln x  a a. 这就是指数函数的导数公式.特殊地,当a=e时,因lne=1, 故有. (e x) ′ = e x