
第三章 单纯形方法 §1 单纯形方法原理 §2 两阶段法与大M法 §3 退化情形 §4 修正单纯形法
第三章 单纯形方法 ◼ §1 单纯形方法原理 ◼ §2 两阶段法与大M 法 ◼ §3 退化情形 ◼ §4 修正单纯形法

§1单纯形法的基本原理 单纯形法(Simplex Method)是1947 年由G.B.Dantig提出,是解LP问 题最有效的算法之一,且已成为整数 规划和非线性规划某些算法的基础。 基本思路: 基于LP问题的标准形式,先设法找到一个基可 行解,判断它是否是最优解,如果是则停止计算;否 则,则转换到相邻的目标函数值不减的一个基可行解 (两个基可行解相邻是指它们之间仅有一个基变量不 相同)
§1 单纯形法的基本原理 单纯形法(Simplex Method)是1947 年由 G.B. Dantzig 提出,是解 LP 问 题最有效的算法之一,且已成为整数 规划和非线性规划某些算法的基础。 基本思路: 基于 LP 问题的标准形式,先设法找到一个基可 行解,判断它是否是最优解,如果是则停止计算;否 则,则转换到相邻的目标函数值不减的一个基可行解. (两个基可行解相邻是指它们之间仅有一个基变量不 相同)

第三章 单纯形法 单纯形法引例 minf=-15x1-25x2+0x3+0x4 s.t. x1+3x2+X3 =60 首先,化原问 X1+X2 +x4=40 题为标准形式: X1,X2,X3,X4≥0 =(PiP.Ps-Pa) B=(P,P4)是可行基, x,x4是基变量. 是最优解吗 基变量用非基变量表示: x3=60-x1-3x2 x4=40-x1-X2 代入目标函数:f=-15x125x2 令非基变量x1=x20f-0基可行解x和=(0,0,60,40)
第三章 单纯形法 单纯形法引例 首先,化原问 题为标准形式: ( 1 2 3 4 ) 1 3 1 0 , , , 1 1 0 1 A p p p p = = x3 , x4 是基变量. B p p = ( 3 4 , )是可行基, 基变量用非基变量表示: x3 = 60 -x1 - 3x2 x4 = 40 -x1 - x2 代入目标函数: f = -15 x1 -25 x2 令非基变量 x1= x2=0 f=0 基可行解 x (0)=(0,0,60,40)T 是最优解吗? max z = 15x1 +25x2 s.t. x1 + 3x2 ≤ 60 x1 + x2 ≤ 40 x1,x2 ≥ 0 min f = -15x1 - 25x2 + 0x3 + 0x4 s.t. x1 + 3x2 + x3 = 60 x1 + x2 + x4=40 x1,x2 , x3 , x4≥ 0

§1.1单纯形法的基本原理 f=-15x1-25x2 因为x2的系数小,所以x2换入基变量。 x3=60-x1-3x2 谁换出? x3=60-3x2≥0 x4=40-x1-X2 x4=40-x2≥0 如果x4换出,则x2=40,x3=60,不可行。 如 2=20,x4=20。 小于零! 0 40 13 20所以x3换出。 最小比值法则 基变量用非基变量表示: x=20-⅓x-⅓x x4=20-2⅓x+⅓x 代入目标函数:f=-50020/3)x1+25/3x3 令非基变量x1=x30 f=-300 基可行解x=(0,20,0,20)
§1.1 单纯形法的基本原理 f = -15 x1 -25 x2 x3 = 60 -x1 - 3x2 x4 = 40 -x1 - x2 因为x2 的系数小,所以x2 换入基变量。 x3 = 60 - 3x2 ≥ 0 x4 = 40 - x2 ≥ 0 谁换出? 如果 x4 换出,则x2 = 40, x3 = -60,不可行。 如果 x3 换出,则x2 = 20, x4 = 20。 2 60 40 min , 20 3 1 x = = 取 所以 x3 换出。 最小比值法则 基变量用非基变量表示: 2 1 3 4 1 3 20 1 1 3 3 20 2 1 3 3 x x x x x x = − − = − + 代入目标函数: f = -500-20/3 x1+ 25/3 x3 令非基变量 x1= x3=0 f= -500 基可行解 x (1)=(0,20,0,20)T 小于零!

第三章 单纯形法 f=-500-23x+253x 因为x1的系数小,所以x1换入基变量 2020 x=20-为x-为x 因 x=min 323 =30 x=20-23x+⅓x 所以x4换出。 x=30+x-32x。 基变量用非基变量表示: x=10-5x+5x 代入目标函数: f=-700+5x3+10x4 令非基变量x3=x4=0 f-700基可行解x2=(30,10,0,0) 因为非基变量的系数都大于零, 所以 x2=(30,10,0,0)T是最优解 fmim=-700,2ma=700
第三章 单纯形法 1 3 2 1 3 4 1 3 20 25 500 3 3 20 1 1 3 3 20 2 1 3 3 f x x x x x x x x = − − + = − − = − + 因为x1 的系数小,所以x1 换入基变量。 1 20 20 min , 30 1 2 3 3 x = = 因 所以 x4 换出。 基变量用非基变量表示: 1 3 4 2 3 4 30 1 3 2 2 10 1 1 2 2 x x x x x x = + − = − + 代入目标函数: f = -700 + 5 x3 +10 x4 令非基变量 x3= x4=0 f=-700 基可行解 x (2)=(30,10,0,0)T 因为非基变量的系数都大于零, 所以 x (2)=(30,10,0,0)T 是最优解 fmin =-700,zmax=700
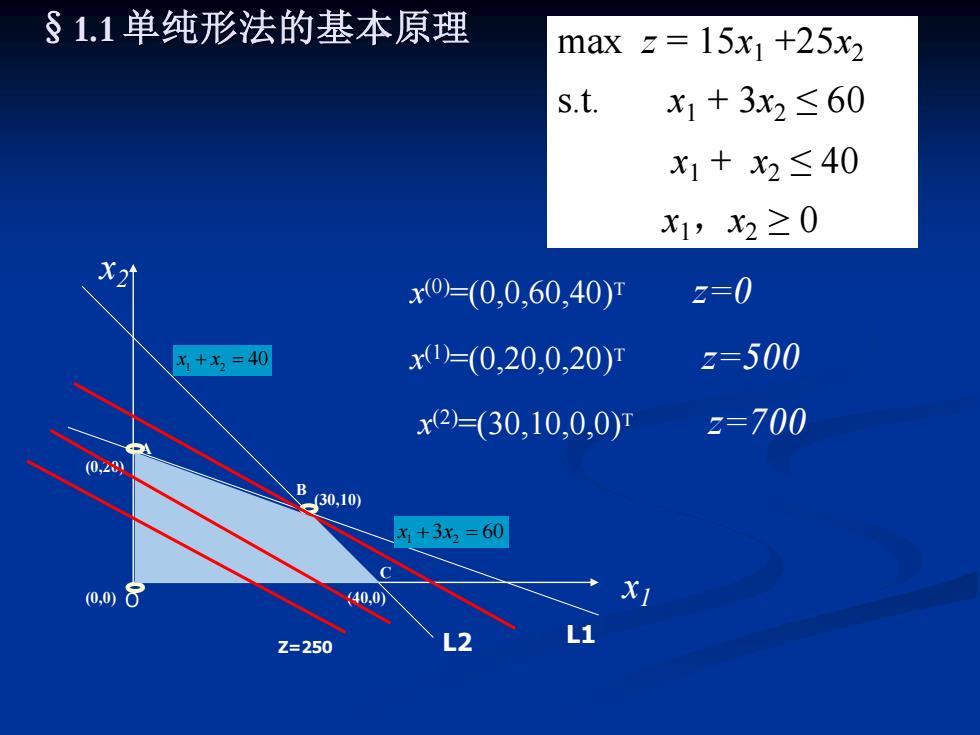
§1.1单纯形法的基本原理 max z=15x1+25x2 s.t. x1+3x2≤60 x1+x2≤40 x1,x2≥0 x x0)=(0,0,60,40)月 z=0 x+x2=40 x1)=(0,20,0,20)月 z=500 x2=(30,10,0,0) z=700 (0,2 B 130,10 x1+3x2=60 ,08 400の X1 Z=250 L1
§1.1 单纯形法的基本原理 (0,0) (40,0) (0,20) A B C (30,10) 1 2 x x + = 3 60 1 2 x x + = 40 O L2 L1 Z=250 x2 x1 x (0)=(0,0,60,40)T z=0 x (1)=(0,20,0,20)T z=500 x (2)=(30,10,0,0)T z=700 max z = 15x1 +25x2 s.t. x1 + 3x2 ≤ 60 x1 + x2 ≤ 40 x1,x2 ≥ 0

第三章 单纯形法 单纯形法的基本原理 min z=CpBb-(CBB N-CN)xN (la) min Z=CX (1) s.t. X8+B Nxy =B-b (2a s.t. Ax=b (2) xB≥0,xw≥0 (3a x≥0 (3) A=(a) 秩() 称(1a)2a)(3a为LP问题对应于 -m 基B的典则形式(典式), Ax=b BXB+NxN =b 基变量用非基变量表示:xB+BNxw=Bb→xB=Bb-BNxN 代入目标函数: ae =CBXB+CNXN- =CB(Bb-BNxN)+CNXN =CBBb-(CBBN-CN )xN
第三章 单纯形法 单纯形法的基本原理 ( ) min (1) . . (2) 0 (3) ij m n z cx s t Ax b x A a A m = = = 秩( )= 1 1 1 1 min ( ) (1 ) . . (2 ) 0, 0 (3 ) B B N N B N B N z c B b c B N c x a s t x B Nx B b a x x a − − − − = − − + = 称(1a)(2a)(3a)为LP问题对应于 基 B 的典则形式(典式). Ax = b Bx Nx b B N + = 基变量用非基变量表示: 1 1 B N x B Nx B b − − + = 1 1 B N x B b B Nx − − = − 代入目标函数: ( ) 1 1 1 1 , ( ) ( ) B B N B B N N N B N N N B B N N x z cx c c c x c x x c B b B Nx c x c B b c B N c x − − − − = = = + = = − + = − −

§1.1单纯形法的基本原理 如果记 2(0)CpB-'b j=CBBPj-C) ON=(Om+1,0。+2,,OO=CsB●-Cw =CBP,-C,=2-C) N'=BN- mm+l mn b=Bb=(b,…,b,n)了则典式(1a)(2a)3a)可写成 min三=z0)-Om+1xm+1-Om+2X+2--可nXn S.t.x1+aim+1m+aim+2Xm+2++ainxn =b X2 a2m+iXm+l a2m+2Xm*2++aznXn =b2 Xm+amm+1mamm+2%m2+amnxn=bm x,≥0 (j=1,2,.,n)
§1.1 单纯形法的基本原理 如果记 (0) 1 B z c B b− = 1 1 2 ( , , , ) N m m n B N c B N c − = = − + + ' ' 1 1 1 ' 1 ' ' 1 ' ' 1 ( , , ) m n m n mm mn a a N B N p p a a + − + + = = = ' 1 ' ' 1 ( , , )T m b B b b b − = = 则典式(1a)(2a)(3a) 可写成 (0) 1 1 2 2 ' ' ' ' 1 1 1 1 1 2 2 1 1 ' ' ' ' 2 2 1 1 2 2 2 2 2 ' ' ' ' 1 1 2 2 min . . 0 ( 1,2, , ) m m m m n n m m m m n n m m m m n n m mm m mm m mn n m j z z x x x s t x a x a x a x b x a x a x a x b x a x a x a x b x j n + + + + + + + + + + + + + + + + = − − − − + + + + = + + + + = + + + + = = 1 ' j B j j B j j j j c B p c c p c z c − = − = − = −

第三章 单纯形法 min 2=20-∑6x (1b) j=m+1 定理7在LP问题 s.t. (2b) 的典式(1b)~(3b)中, x+∑ax,=6i=1,2,m 1=1+] 如果有 x,≥0(j=1,2,,n) (3b) o,≤0(j=m+1,m+2,n 则对应于基B的基可行解 x0=(6,b2,…,bn,0,…,0) 是LP问题的最优解,记为 x=(6,b,…,bn0,…,0) 相应的目标函数最优值 z*=20) 此时,基B 称 =(OB,ON)=CBBA-c=(0,cBB N-CN) 为最优基
第三章 单纯形法 (0) 1 ' ' 1 min (1 ) . . ( 1,2, , ) (2 ) 0 ( 1,2, , ) (3 ) n j j j m n i ij j i j m j z z x b s t x a x b i m b x j n b = + = + = − + = = = 定理 7 在 LP 问题 的典式 (1b) ~(3b)中, 如果有 0 ( 1, 2, , ) j = + + j m m n 则对应于基 B 的基可行解 (0) ' ' ' 1 2 ( , , , ,0, ,0)T m x b b b = 是 LP 问题的最优解,记为 ' ' ' 1 2 ( , , , ,0, ,0)T m x b b b = 相应的目标函数最优值 z * =z(0) 此时,基B 称 = = − = − ( B N B B N , 0, ) c B A c c B N c − − 1 1 ( ) 为最优基

§1.1单纯形法的基本原理 定理8在LP问题 min z=z0)- ∑o,x (1b) j=m+ 的典式(1b)~(3b)中 st.x+∑a,x,=b (=1,2,…,m (2b) j=1+1 x9=(6,,bn,00 x,≥0 (U=1,2,…,n) (3b) 是对应于基B的一个基可行解, 如果满足下列条件: (1)有某个非基变量x,的检验数ok>0(+1≤k≤ (2)a'=1,2,.,m)不全小于或等于零,即至少有一个 a'i20(=1,2,.,ml; (3)b今0(=1,2,,m),即x0)为非退化的基可行解。 则从x0出发,一定能找到一个新的基可行解 x"=(3"”x”》 使得 cr
§1.1 单纯形法的基本原理 定理 8 在 LP 问题 的典式 (1b) ~(3b)中, (0) 1 ' ' 1 min (1 ) . . ( 1,2, , ) (2 ) 0 ( 1,2, , ) (3 ) n j j j m n i ij j i j m j z z x b s t x a x b i m b x j n b = + = + = − + = = = ( ) ( ) 0 ' ' 1 , , ,0, ,0 T m x b b = 是对应于基 B 的一个基可行解,如果满足下列条件: (1)有某个非基变量 xk 的检验数 σk >0 (m+1 ≤ k ≤n); (2)a’ik(i=1,2,…,m) 不全小于或等于零,即至少有一个 a’ik>0 (i=1,2,…,m) ; (3) >0 (i=1,2,…,m) ,即x (0) 为非退化的基可行解。 ' i b 则从 x (0)出发,一定能找到一个新的基可行解 ( ) (1) (1) (1) (1) (1) (0) 1 2 , , , . T n x x x x cx cx = 使得 <