
统计学 第九章 相关与回归 相关和回归分析是研究事物的相互关系、 测定它们联系的紧密程度、揭示其变化的 具体形式和规律性的统计方法,是经济分 析、预测和控制的重要工具
第九章 相关与回归 相关和回归分析是研究事物的相互关系、 测定它们联系的紧密程度、揭示其变化的 具体形式和规律性的统计方法,是经济分 析、预测和控制的重要工具

第一节相关与回归分析的基本问题 相关的概念与种类 函数关系 现象之间确实存在数量上的相互依存关系。 表现在:一个现象发生数量上的变化,另 个与之相联系的现象也会相应地发生数 量上的变化。 相关关系 现象之间数量上不确定、不严格的依存关 系。相关关系的全称为统计相关关系,它 属于变量之间的一种不完全确定的关系
第一节 相关与回归分析的基本问题 一、相关的概念与种类 ◼ 函数关系 – 现象之间确实存在数量上的相互依存关系。 表现在:一个现象发生数量上的变化,另 一个与之相联系的现象也会相应地发生数 量上的变化。 ◼ 相关关系 – 现象之间数量上不确定、不严格的依存关 系。相关关系的全称为统计相关关系,它 属于变量之间的一种不完全确定的关系

比较下面两种现象间的依存关系 统计学 函数关系 1. 出租汽车费用与行驶里积 (确定性关系) 总费用=行驶里程×每公里单价 G=K×P 相关关系 (非确定性关系) 2.家庭收入与恩格尔多” 家庭收入高,则恩格尔系数低
⒈ 出租汽车费用与行驶里程: 总费用=行驶里程 每公里单价 G = KP ⒉ 家庭收入与恩格尔系数: 家庭收入高,则恩格尔系数低。 函数关系 (确定性关系) 相关关系 (非确定性关系) 比较下面两种现象间的依存关系

统计学 相关关系与函数关系的区别 函数关系是变量之间的一种严格、完全确 定性的关系,即一个变量的数值完全有另 一 个(或一组)变量的数值所决定、控制。 函数关系通常可以用数学公式确切地表示 出来。 相关关系难以像函数关系那样,用数学公 式去准确表达
◼ 相关关系与函数关系的区别 ◼ 函数关系是变量之间的一种严格、完全确 定性的关系,即一个变量的数值完全有另 一个(或一组)变量的数值所决定、控制。 函数关系通常可以用数学公式确切地表示 出来。 ◼ 相关关系难以像函数关系那样,用数学公 式去准确表达

统计学 相关关系与函数关系的联系 由于客观上常会出现观察或测量上的误差 等原因,函数关系在实际工作中往往通过相 关关系表现出来。当人们对某些现象内部规 律有较深刻认识时,相关关系可能变为函数 关系。为此,在研究相关关系时,又常常使 用函数关系作为工具,用一定的函数关系表 现相关关系的数量联系
◼ 相关关系与函数关系的联系 ◼ 由于客观上常会出现观察或测量上的误差 等原因,函数关系在实际工作中往往通过相 关关系表现出来。当人们对某些现象内部规 律有较深刻认识时,相关关系可能变为函数 关系。为此,在研究相关关系时,又常常使 用函数关系作为工具,用一定的函数关系表 现相关关系的数量联系
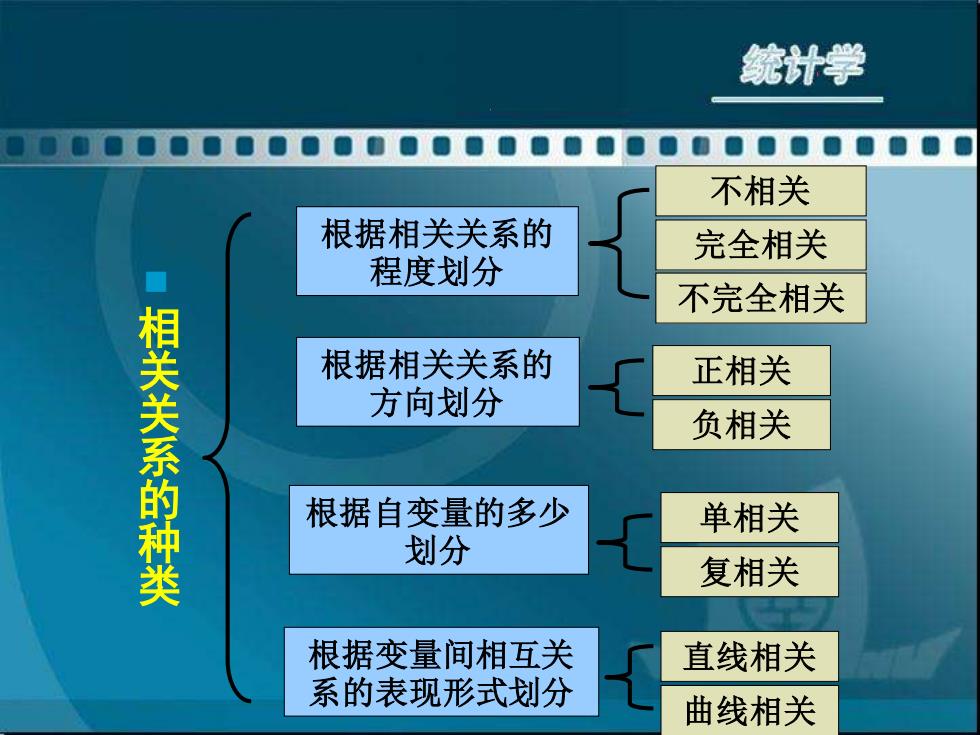
统计学 不相关 根据相关关系的 完全相关 程度划分 不完全相关 相关关系的种类 根据相关关系的 正相关 方向划分 负相关 根据自变量的多少 单相关 划分 复相关 根据变量间相互关 直线相关 系的表现形式划分 曲线相关
◼ 相关关系的种类 根据相关关系的 程度划分 根据相关关系的 方向划分 根据自变量的多少 划分 根据变量间相互关 系的表现形式划分 不完全相关 完全相关 不相关 正相关 负相关 复相关 单相关 直线相关 曲线相关

·根据相关关系的程度划分 统计学 1、不相关。如果变量间彼此的数量变化互相独立,则其关系为不相 关。自变量x变动时,因变量y的数值不随之相应变动。例如,产品税 额的多少与工人的出勤率、家庭收入多少与孩子的多少之间都不存在 相关关系。 2、完全相关。如果一个变量的变化是由其他变量的数量变化所唯一 确定,此时变量间的关系称为完全相关。即因变量y的数值完全随自 变量x的变动而变动,它在相关图上表现为所有的观察点都落在同一 条直线上,这种情况下,相关关系实际上是函数关系。所以,函数关 系是相关关系的一种特殊情况。 3、不完全相关。如果变量间的关系介于不相关和完全相关之间,则 称为不完全相关。如妇女的结婚年龄与受教育程度之间的一种关系。 大多数相关关系属于不完全相关,是统计研究的主要对象
1、不相关。 如果变量间彼此的数量变化互相独立,则其关系为不相 关。自变量x变动时,因变量y的数值不随之相应变动。例如,产品税 额的多少与工人的出勤率、家庭收入多少与孩子的多少之间都不存在 相关关系。 2、完全相关。如果一个变量的变化是由其他变量的数量变化所唯一 确定,此时变量间的关系称为完全相关。即因变量y的数值完全随自 变量x的变动而变动,它在相关图上表现为所有的观察点都落在同一 条直线上,这种情况下,相关关系实际上是函数关系。所以,函数关 系是相关关系的一种特殊情况。 3、不完全相关。如果变量间的关系介于不相关和完全相关之间,则 称为不完全相关。如妇女的结婚年龄与受教育程度之间的一种关系。 大多数相关关系属于不完全相关,是统计研究的主要对象 ▪根据相关关系的程度划分

·根据相关关系的方向划分 统计学 0 1、正相关。指两个因素(或变量)之间的变化方向一致 都是皇增长或下降的趋势。即自变量x的值增加(或减 少),因变量y的值也相应地增加(或减少),这样的关 系就是正相关。例如,工业总产值增加,企业税利总额也 随之增加;家庭消费支出随收入增加而增加等。 2、 负相关。指两个因素或变量之间变化方向相反,即自 变量的数值增大(或减小),因变量随之减小(或增大) 如劳动生产率提高,产品成本降低;产品成本降低,企业 刹润增茄等
1、正相关。指两个因素(或变量)之间的变化方向一致, 都是呈增长或下降的趋势。即自变量x的值增加(或减 少),因变量y的值也相应地增加(或减少),这样的关 系就是正相关。例如,工业总产值增加,企业税利总额也 随之增加;家庭消费支出随收入增加而增加等。 2、负相关。指两个因素或变量之间变化方向相反,即自 变量的数值增大(或减小),因变量随之减小(或增大)。 如劳动生产率提高,产品成本降低;产品成本降低,企业 利润增加等。 ▪根据相关关系的方向划分

·根据自变量的多少划分 统计学 1、单相关。两个因素之间的相关关系叫单相关, 即研究时只涉及一个自变量和一个因变量。 2、复相关。三个或三个以上因素的相关关系叫 复相关,即研究时涉及两个或两个以上的自变 量和因变量
1、单相关。两个因素之间的相关关系叫单相关, 即研究时只涉及一个自变量和一个因变量。 2、复相关。三个或三个以上因素的相关关系叫 复相关,即研究时涉及两个或两个以上的自变 量和因变量。 ▪根据自变量的多少划分

·根据变量间相互关系的表现形式划分 00■ 1、直线相关(或线性相关)。当相关关系的自变量x发生变 动,因变量y值随之发生大致均等的变动,从图像上近似 地表现为直线形式,这种相关通称为直线(或线性)相关。 例如,销售量与销售额之间就呈直线相关关系。 2、曲线(或非线性)相关。在两个相关现象中,自变量x值 发生变动,因变量y也随之发生变动,这种变动不是均等 的,在图像上的分布是各种不同的曲线形式,这种相关关 系称为曲线(或非线性)相关。曲线相关在相关图上的分 布,表现为抛物线、双曲线、指数曲线等非直线形式。例 如,从人的生命全过程看,年龄与医疗费支出呈非线性相 关
1、直线相关(或线性相关)。当相关关系的自变量x发生变 动,因变量y值随之发生大致均等的变动,从图像上近似 地表现为直线形式,这种相关通称为直线(或线性)相关。 例如,销售量与销售额之间就呈直线相关关系。 2、曲线(或非线性)相关。在两个相关现象中,自变量x值 发生变动,因变量y也随之发生变动,这种变动不是均等 的,在图像上的分布是各种不同的曲线形式,这种相关关 系称为曲线(或非线性)相关。曲线相关在相关图上的分 布,表现为抛物线、双曲线、指数曲线等非直线形式。例 如,从人的生命全过程看,年龄与医疗费支出呈非线性相 关。 ▪根据变量间相互关系的表现形式划分