
第9章直线相关与回归目录 第一节直线相关 第二节直线回归 口第三节相关回归分析注意问题 口第四节等级相关 口第五节曲线直线化 筒历 返回总目绿 返回章耳录口口 第9章直线相关与回归 第5页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第5页 第9章 直线相关与回归 目录 ❑ 第五节 曲线直线化 ❑ 第二节 直线回归 ❑ 第三节 相关回归分析注意问题 ❑ 第四节 等级相关 ❑ 第一节 直线相关

第9章 直线相关与回归学习要求 1. 掌握:直线相关与回归的概念及意义。 2.掌握:直线相关与回归系数的适用条件、计算及 检验方法。 3.熟悉:直线相关与回归分析时应注意的问题。 4.熟悉:等级相关的概念、意义、适用条件及计算 方法。 5.了解:曲线直线化的概念、意义及计算方法。 筒历 返回总目录返回章目录口>口结束 第9章直线相关与回归 第6页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第6页 第9章 直线相关与回归 学习要求 1. 掌握:直线相关与回归的概念及意义。 2. 掌握:直线相关与回归系数的适用条件、计算及 检验方法。 3. 熟悉:直线相关与回归分析时应注意的问题。 4. 熟悉:等级相关的概念、意义、适用条件及计算 方法。 5. 了解:曲线直线化的概念、意义及计算方法

第一节直线相关 相关的概念: 两事物或现象在数量上的协同变化呈直线趋势时 则称为直线相关(linear correlation),又称简 单相关(simple correlation),用于分析双变 量正态分布资料。表示两变量相关关系的重要指 标就是相关系数。 简历 返回总目录 返回章目录 结束 第9章直线相关与回归 第7页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第7页 第一节 直线相关 相关的概念: 两事物或现象在数量上的协同变化呈直线趋势时 则称为直线相关(linear correlation),又称简 单相关(simple correlation),用于分析双变 量正态分布资料。表示两变量相关关系的重要指 标就是相关系数

一、相关系数的意义 1. 相关系数(correlation coefficient)又称为积差相关系 数,用符号表示。 2. 它描述两变量间相关关系的密切程度和相关方向。其数 值1≥r2-1,当为正值时,表示一变量随另一变量的增 加而增加称为正相关:当为负值时,表示一变量随另一 变量的增加而减少,称为负相关。 3. 当|r愈接近1,表示两变量的相关愈密切;当r愈接 近0时,表示两变量相关程度愈低;当r=0时,称为 零相关,表示两变量无直线相关关系,见示意图9-1。 筒历 返回总目录 返回章录口 结束 第9章直线相关与回归 第8页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第8页 1. 相关系数(correlation coefficient)又称为积差相关系 数,用符号r表示。 2. 它描述两变量间相关关系的密切程度和相关方向。其数 值1≥r≥-1,当r为正值时,表示一变量随另一变量的增 加而增加称为正相关;当r为负值时,表示一变量随另一 变量的增加而减少,称为负相关。 3. 当│r│愈接近1,表示两变量的相关愈密切;当│r│愈接 近0时,表示两变量相关程度愈低;当│r│=0时,称为 零相关,表示两变量无直线相关关系,见示意图9-1。 一、相关系数的意义

相关程度的判断 般认为,当样本含量较大的情况下(n>100), 大致可按下列标准估计两变量相关的程度 ● 1rl≥0.7 高度相关 0.7>1rl≥0.4 中度相关 0.4>r≥0.2 低度相关 简历 返回总目绿 返回章耳录4口>口结束 第9章直线相关与回归 第9页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第9页 一般认为,当样本含量较大的情况下(n>100), 大致可按下列标准估计两变量相关的程度 • │r│≥0.7 高度相关 • 0.7>│r│≥0.4 中度相关 • 0.4>│r│≥0.2 低度相关 相关程度的判断
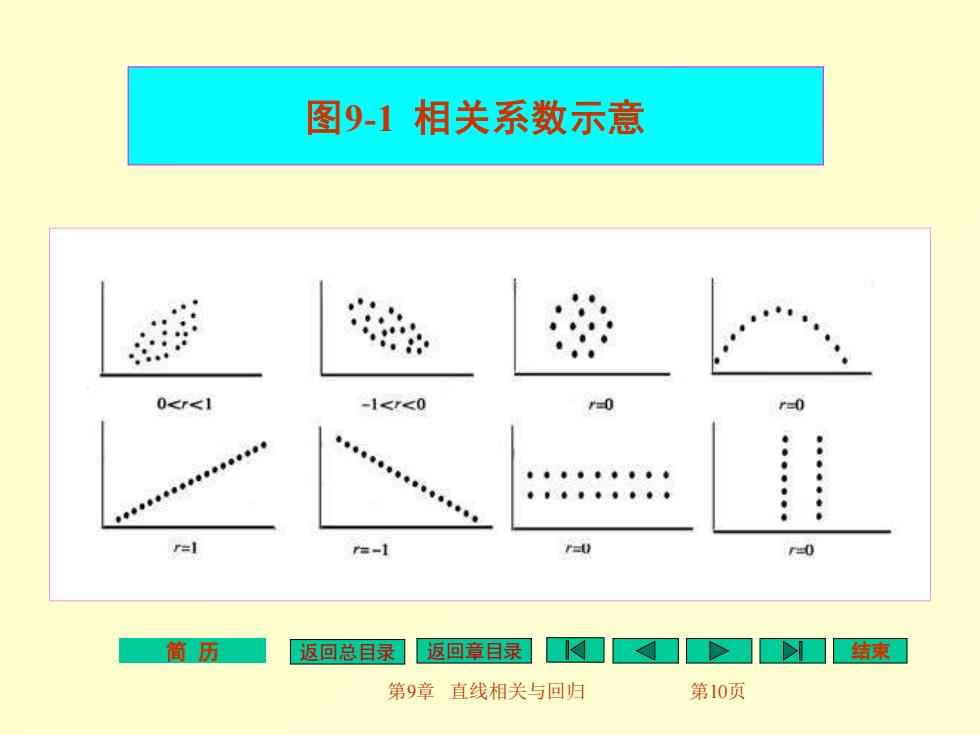
图91相关系数示意 . 0口[ 结束 第9章直线相关与回归 第10页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第10页 图9-1 相关系数示意

二、相关系数的计算 相关系数的计算公式: ∑(X-X)Y-Y) V2(X-X)2V∑(Y-72V1xV 式中:lxx与ly分别为变量X与Y的离均差平方和 lxy为两变量X、Y的离均差积和。 筒历 返回总目绿 返回章目录4口>口结束 第9章直线相关与回归 第11页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第11页 相关系数r的计算公式: 二、相关系数的计算 X X YY X Y l l l X X Y Y X X Y Y r = − − − − = 2 2 ( ) ( ) ( )( ) 式中:lXX与lYY分别为变量X与Y的离均差平方和, lXY为两变量X 、Y的离均差积和

请牢记下列计算公式: 1x=∑X2 _(②)2 =∑y2-(②)2 n n ly=∑XY- (∑X)∑Y) n 筒历 返回总目录返回章目录口>口结束 第9章直线相关与回归 第12页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第12页 请牢记下列计算公式: n X l XX X 2 2 ( ) = − n Y l YY Y 2 2 ( ) = − n X Y l X Y XY ( )( ) = −

实例分析 1. 【例9.1】某研究者测量10名20岁男青年身高 与前臂长。数据见表9-1。试分析:身高与前臂 长有无直线相关关系? 2.计算步骤: 3.(1)由原始数据绘制散点图9-2,本资料呈直 线相关趋势。 筒历 返回总目录 返回章目录口>口结求 第9章直线相关与回归 第13页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第13页 1. 【例9.1 】某研究者测量10名20岁男青年身高 与前臂长。数据见表9-1。试分析:身高与前臂 长有无直线相关关系? 2. 计算步骤: 3. (1)由原始数据绘制散点图9-2,本资料呈直 线相关趋势。 实例分析
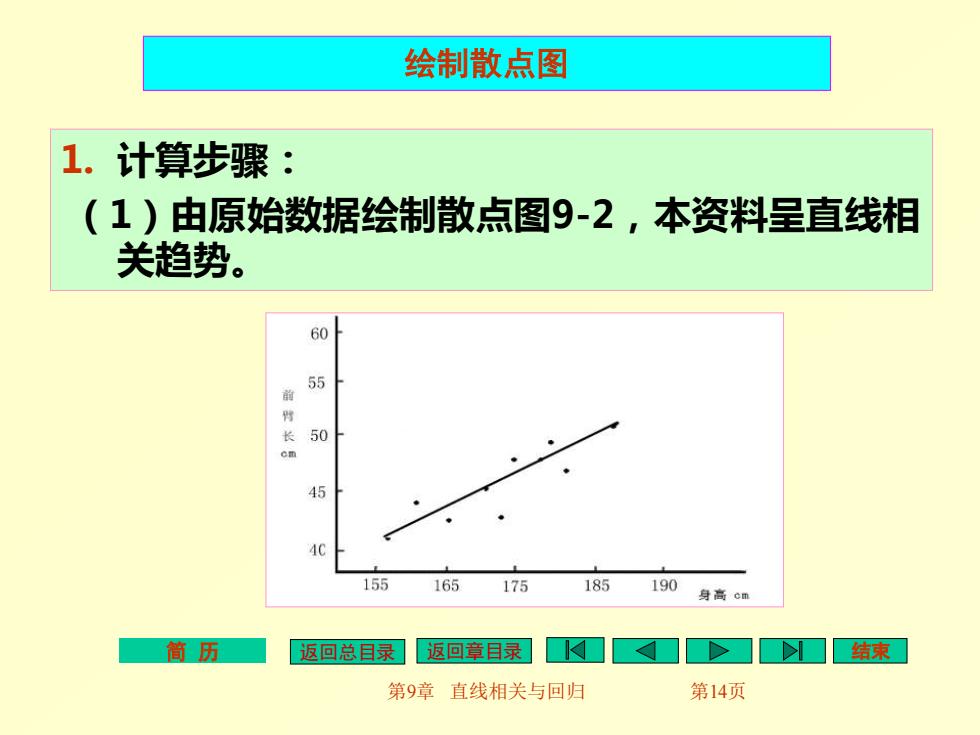
绘制散点图 1.计算步骤: (1)由原始数据绘制散点图9-2,本资料呈直线相 关趋势。 60 55 长 50 45 155 165175 185190 身高心m 筒历 返回总目录 返回章目录]口>口结束 第9章直线相关与回归 第14页
简 历 返回总目录 返回章目录 结束 第9章 直线相关与回归 第14页 1. 计算步骤: (1)由原始数据绘制散点图9-2,本资料呈直线相 关趋势。 绘制散点图