
第七章 统计推断包括参数估计和假设 检验,即通过样本统计量来估计和 样推断 检验总体的参数。统计推断的目的 在于认识未知的总体参数及其分布 特征
统计推断包括参数估计和假设 检验,即通过样本统计量来估计和 检验总体的参数。统计推断的目的 在于认识未知的总体参数及其分布 特征。 第七章 抽 样 推 断

§1.点估计 参数估计有点估计和区间估计。 一、点估计 点估计是通过计算一个统计量(样本元素的函 数),将它作为未知参数的估计。 样本 统计量 未知参数 X,X→0=dX,X)→ 0 对一次具体的抽样 观察值O=d(x1,.,xn)
§1. 点 估 计 一、点估计 点估计是通过计算一个统计量(样本元素的函 数),将它作为未知参数的估计。 X1 ,., Xn 样本 统计量 未知参数 ( , , ) 1 n = d x x 观察值 对一次具体的抽样 参数估计有点估计和区间估计。 = d (X1 ,., Xn → ) →

二、估计量 1.估计量是用来估计参数的统计量 用来估计参数0的估计量记为 2.点估计量的构造方法常用的有: 矩法和极大似然法(略)
二、估计量 1. 估计量是用来估计参数的统计量 用来估计参数 的估计量 记为 2. 点估计量的构造方法常用的有: 矩法和极大似然法 (略)

例:从平均值为4,标准差为o的总体中抽出样本 K1 In 1若把样本平均数双-X用作4的估计量即=X n ~(X0-E()-E(X)-u-4 .是的无偏估计量
例:从平均值为,标准差为的总体中抽出样本 X1 ,., Xn X n X 若把样本平均数X 用作 的估计量 即 = 1 = , i = = = = n n E X n n X E X E 1 ( ) 1 ( ) ( ) i i X是的无偏估计量

3.点估计量优劣的判别标准 衡量一个估计量好坏的标准通常有以下3个: (1)无偏性: 如果一个估计量的数学期望值等于被估计 参数,则这个估计量称为被估参数的无偏估计 量。也就是说: 若E(0)=0,则0为的无偏估计量
3. 点估计量优劣的判别标准 衡量一个估计量好坏的标准通常有以下3个: (1) 无偏性: 如果一个估计量的数学期望值等于被估计 参数,则这个估计量称为被估参数的无偏估计 量。也就是说: 若 则 为的无偏估计量。 E( ) =
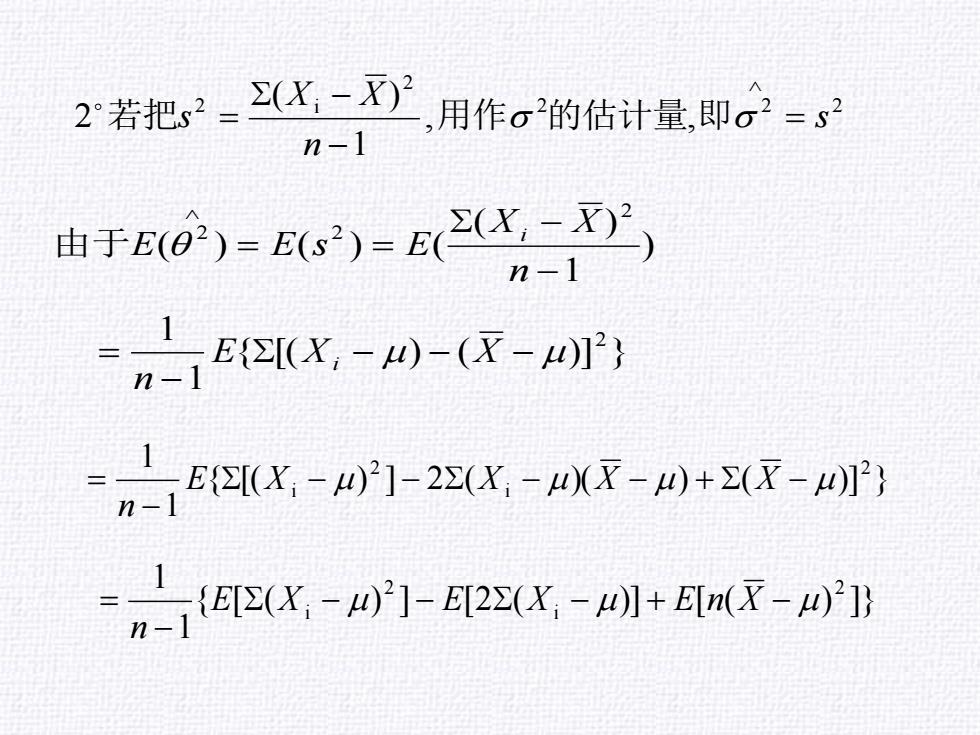
2若把5_2(X-),用作o的估计量,即。=9 n-1 由时no)) =1E8[X,-)-(-w]) n-1 4X-1-2X-Xx-wT时 X-1-H2AI+a-
2 2 2 2 2 i , , 1 ( ) 2 s n X X s = − − = 若把 用作 的估计量 即 ) 1 ( ) ( ) ( ) ( 2 2 2 − − = = n X X E E s E i 由于 { [( ) ( )] } 1 1 2 − − − − = E X X n i { [( ) ] 2 ( )( ) ( )] } 1 1 2 i 2 i − − − − + − − = E X X X X n { [ ( ) ] [2 ( )] [ ( ) ]} 1 1 2 i 2 i − − − + − − = E X E X E n X n
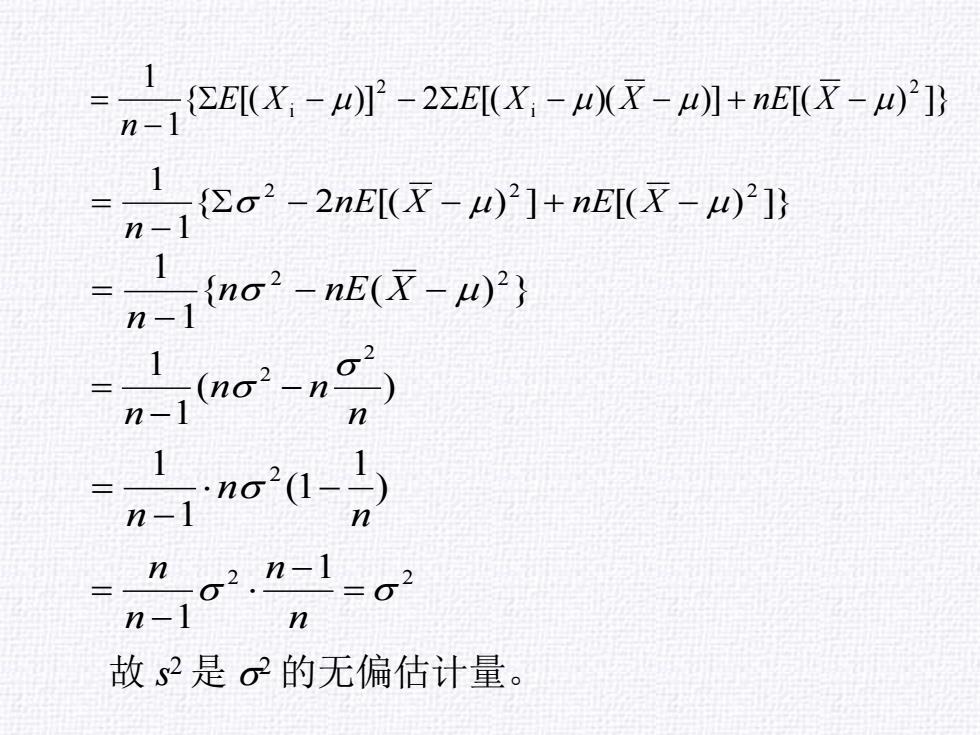
sx-2zU-AX7-+nGT-A 72o2n]+nx0ny n-1 (no2-nE(X-u)2) (ng'-n) n-1 na2.n-1=o2 n-1 n 故s2是o2的无偏估计量
{ 2 [( ) ] [( ) ]} 1 1 2 2 2 − − + − − = nE X nE X n { [( )] 2 [( )( )] [( ) ]} 1 1 2 i 2 i − − − − + − − = E X E X X nE X n { ( ) } 1 1 2 2 − − − = n nE X n ( ) 1 1 2 2 n n n n − − = ) 1 (1 1 1 2 n n n − − = 2 1 2 1 = − − = n n n n 故 s 2 是 的无偏估计量
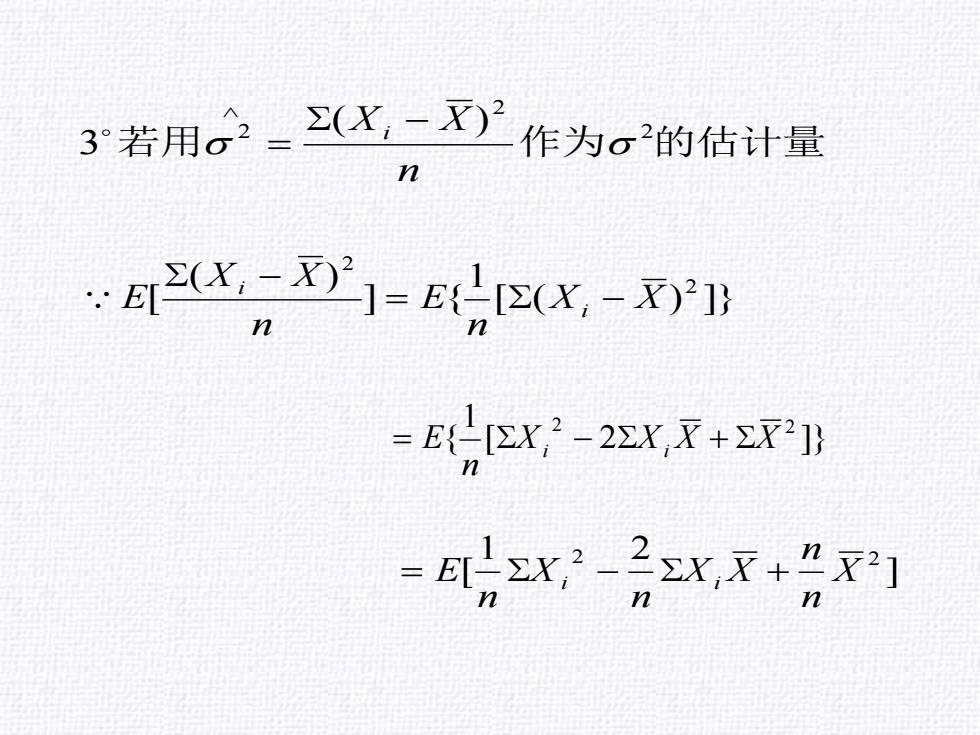
3若用。_(X,一)作为。的估计量 n aW]=0x-X =(zx2-2xxx+zX]》 =x,-x,x+x]
若用 作为 2 的估计量 2 2 ( ) 3 n Xi − X = [ ( ) ]} 1 ] { ( ) [ 2 2 X X n E n X X E i i = − − ] 1 2 [ 2 2 X n n X X n X n = E i − i + [ 2 ]} 1 { 2 2 X X X X n = E i − i +
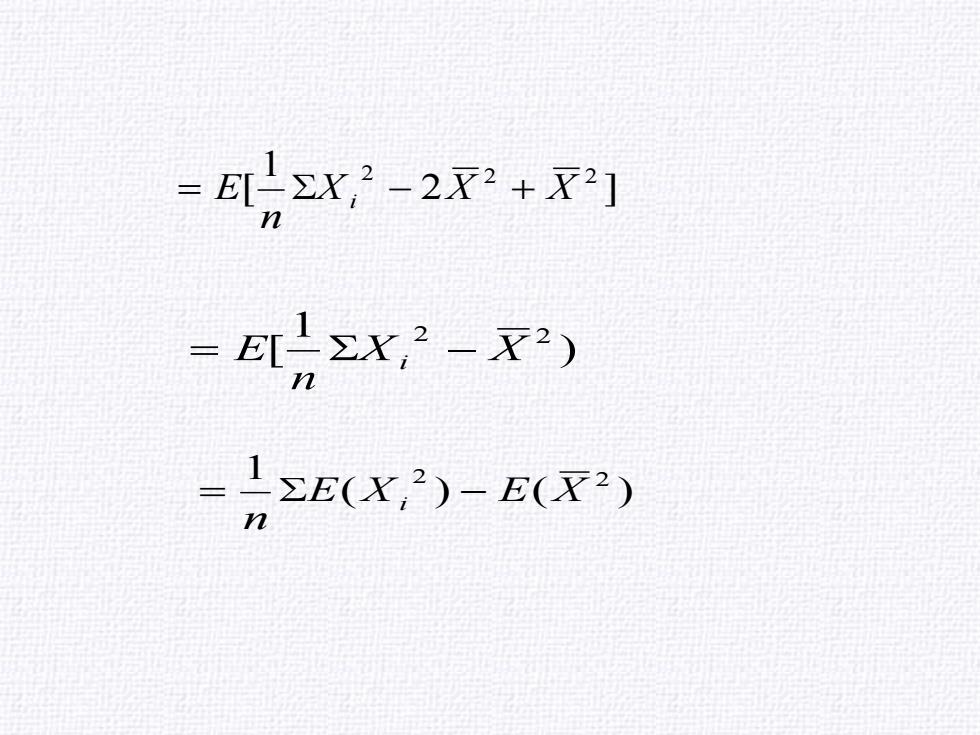
=EzX,2-2X2+x2] =Σ,) =1ΣE(x,2)-EX2) n
2 ] 1 [ 2 2 2 X X X n = E i − + ) 1 [ 2 2 X X n = E i − ( ) ( ) 1 2 2 E X E X n = i −
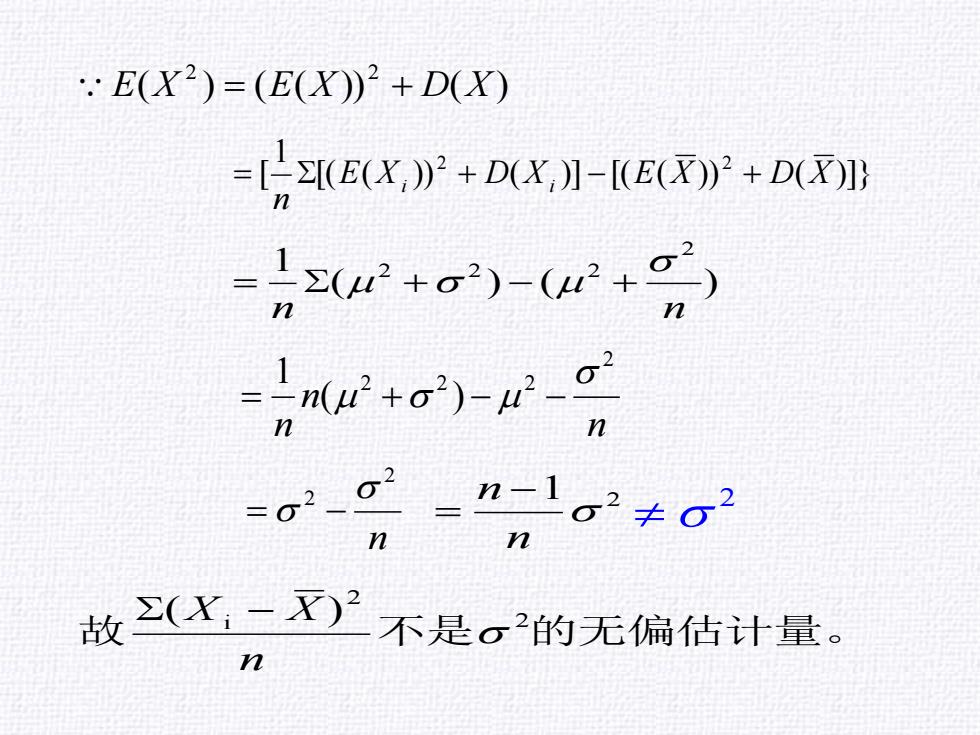
.·E(X2)=(E(X)2+D(X) -月E(X,》P+DX,】-(EN+D +o)-2+ nd- =02-g-n-1.2≠2 n n 故(X,-)不是。的无偏估计量。 n
( ) ( ( )) ( ) 2 2 E X = E X + D X n n n 2 2 2 2 ( ) 1 = + − − ( ) ( ) 1 2 2 2 2 n n = + − + n 2 2 = − 1 2 n n − = 2 故 不是 2 的无偏估计量。 2 i ( ) n X − X [( ( )) ( )] [( ( )) ( )]} 1 [ 2 2 E X D X E X D X n = i + i − +